Leslie Pack Kaelbling
Michael L. Littman
lpk,mlittman@cs.brown.edu
Computer Science Department, Box 1910,
Brown University
Providence, RI 02912-1910 USA
- Andrew W. Moore
awm@cs.cmu.edu
Smith Hall 221, Carnegie Mellon University, 5000
Forbes Avenue
Pittsburgh, PA 15213 USA
This paper surveys the field of reinforcement learning from a computer-science perspective. It is written to be accessible to researchers familiar with machine learning. Both the historical basis of the field and a broad selection of current work are summarized. Reinforcement learning is the problem faced by an agent that learns behavior through trial-and-error interactions with a dynamic environment. The work described here has a resemblance to work in psychology, but differs considerably in the details and in the use of the word ``reinforcement.'' The paper discusses central issues of reinforcement learning, including trading off exploration and exploitation, establishing the foundations of the field via Markov decision theory, learning from delayed reinforcement, constructing empirical models to accelerate learning, making use of generalization and hierarchy, and coping with hidden state. It concludes with a survey of some implemented systems and an assessment of the practical utility of current methods for reinforcement learning.
Reinforcement learning dates back to the early days of cybernetics and work in statistics, psychology, neuroscience, and computer science. In the last five to ten years, it has attracted rapidly increasing interest in the machine learning and artificial intelligence communities. Its promise is beguiling--a way of programming agents by reward and punishment without needing to specify how the task is to be achieved. But there are formidable computational obstacles to fulfilling the promise.
This paper surveys the historical basis of reinforcement learning and some of the current work from a computer science perspective. We give a high-level overview of the field and a taste of some specific approaches. It is, of course, impossible to mention all of the important work in the field; this should not be taken to be an exhaustive account.
Reinforcement learning is the problem faced by an agent that must learn behavior through trial-and-error interactions with a dynamic environment. The work described here has a strong family resemblance to eponymous work in psychology, but differs considerably in the details and in the use of the word ``reinforcement.'' It is appropriately thought of as a class of problems, rather than as a set of techniques.
There are two main strategies for solving reinforcement-learning problems. The first is to search in the space of behaviors in order to find one that performs well in the environment. This approach has been taken by work in genetic algorithms and genetic programming, as well as some more novel search techniques [101]. The second is to use statistical techniques and dynamic programming methods to estimate the utility of taking actions in states of the world. This paper is devoted almost entirely to the second set of techniques because they take advantage of the special structure of reinforcement-learning problems that is not available in optimization problems in general. It is not yet clear which set of approaches is best in which circumstances.
The rest of this section is devoted to establishing notation and describing
the basic reinforcement-learning model. Section 2
explains the trade-off between exploration and exploitation and presents some
solutions to the most basic case of reinforcement-learning problems, in which we
want to maximize the immediate reward. Section 3
considers the more general problem in which rewards can be delayed in time from
the actions that were crucial to gaining them. Section 4
considers some classic model-free algorithms for reinforcement learning from
delayed reward: adaptive heuristic critic, ![]() and Q-learning. Section 5
demonstrates a continuum of algorithms that are sensitive to the amount of
computation an agent can perform between actual steps of action in the
environment. Generalization--the cornerstone of mainstream machine learning
research--has the potential of considerably aiding reinforcement learning, as
described in Section 6
Section 7
considers the problems that arise when the agent does not have complete
perceptual access to the state of the environment. Section 8
catalogs some of reinforcement learning's successful applications. Finally,
Section 9
concludes with some speculations about important open problems and the future of
reinforcement learning.
and Q-learning. Section 5
demonstrates a continuum of algorithms that are sensitive to the amount of
computation an agent can perform between actual steps of action in the
environment. Generalization--the cornerstone of mainstream machine learning
research--has the potential of considerably aiding reinforcement learning, as
described in Section 6
Section 7
considers the problems that arise when the agent does not have complete
perceptual access to the state of the environment. Section 8
catalogs some of reinforcement learning's successful applications. Finally,
Section 9
concludes with some speculations about important open problems and the future of
reinforcement learning.
In the standard reinforcement-learning model, an agent is connected to its environment via perception and action, as depicted in Figure 1. On each step of interaction the agent receives as input, i, some indication of the current state, s, of the environment; the agent then chooses an action, a, to generate as output. The action changes the state of the environment, and the value of this state transition is communicated to the agent through a scalar reinforcement signal, r. The agent's behavior, B, should choose actions that tend to increase the long-run sum of values of the reinforcement signal. It can learn to do this over time by systematic trial and error, guided by a wide variety of algorithms that are the subject of later sections of this paper.
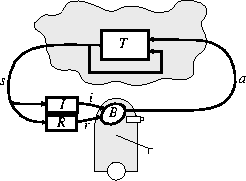
Figure 1: The standard reinforcement-learning model.
Formally, the model consists of
An intuitive way to understand the relation between the agent and its environment is with the following example dialogue.
| Environment: | You are in state 65. You have 4 possible actions. |
| Agent: | I'll take action 2. |
| Environment: | You received a reinforcement of 7 units. You are now in state 15. You have 2 possible actions. |
| Agent: | I'll take action 1. |
| Environment: | You received a reinforcement of -4 units. You are now in state 65. You have 4 possible actions. |
| Agent: | I'll take action 2. |
| Environment: | You received a reinforcement of 5 units. You are now in state 44. You have 5 possible actions. |
Reinforcement learning differs from the more widely studied problem of supervised learning in several ways. The most important difference is that there is no presentation of input/output pairs. Instead, after choosing an action the agent is told the immediate reward and the subsequent state, but is not told which action would have been in its best long-term interests. It is necessary for the agent to gather useful experience about the possible system states, actions, transitions and rewards actively to act optimally. Another difference from supervised learning is that on-line performance is important: the evaluation of the system is often concurrent with learning.
Some aspects of reinforcement learning are closely related to search and planning issues in artificial intelligence. AI search algorithms generate a satisfactory trajectory through a graph of states. Planning operates in a similar manner, but typically within a construct with more complexity than a graph, in which states are represented by compositions of logical expressions instead of atomic symbols. These AI algorithms are less general than the reinforcement-learning methods, in that they require a predefined model of state transitions, and with a few exceptions assume determinism. On the other hand, reinforcement learning, at least in the kind of discrete cases for which theory has been developed, assumes that the entire state space can be enumerated and stored in memory--an assumption to which conventional search algorithms are not tied.
Before we can start thinking about algorithms for learning to behave optimally, we have to decide what our model of optimality will be. In particular, we have to specify how the agent should take the future into account in the decisions it makes about how to behave now. There are three models that have been the subject of the majority of work in this area.
The finite-horizon model is the easiest to think about; at a given moment in time, the agent should optimize its expected reward for the next h steps:
![]()
it need not worry about what will happen after that. In this and subsequent expressions,rf represents the scalar reward received t steps into the future. This model can be used in two ways. In the first, the agent will have a non-stationary policy; that is, one that changes over time. On its first step it will take what is termed a h-step optimal action. This is defined to be the best action available given that it has h steps remaining in which to act and gain reinforcement. On the next step it will take a (h-1)-step optimal action, and so on, until it finally takes a 1-step optimal action and terminates. In the second, the agent does receding-horizon control, in which it always takes the h-step optimal action. The agent always acts according to the same policy, but the value of h limits how far ahead it looks in choosing its actions. The finite-horizon model is not always appropriate. In many cases we may not know the precise length of the agent's life in advance.
The infinite-horizon discounted model takes the long-run reward of the agent
into account, but rewards that are received in the future are geometrically
discounted according to discount factor ![]() , (where
, (where![]() ):
):
![]()
We can interpret ![]() in
several ways. It can be seen as an interest rate, a probability of living
another step, or as a mathematical trick to bound the infinite sum. The model is
conceptually similar to receding-horizon control, but the discounted model is
more mathematically tractable than the finite-horizon model. This is a dominant
reason for the wide attention this model has received.
in
several ways. It can be seen as an interest rate, a probability of living
another step, or as a mathematical trick to bound the infinite sum. The model is
conceptually similar to receding-horizon control, but the discounted model is
more mathematically tractable than the finite-horizon model. This is a dominant
reason for the wide attention this model has received.
Another optimality criterion is the average-reward model, in which the agent is supposed to take actions that optimize its long-run average reward:
![]()
Such a policy is referred to as a gain optimal policy; it can be seen as the limiting case of the infinite-horizon discounted model as the discount factor approaches 1 [14]. One problem with this criterion is that there is no way to distinguish between two policies, one of which gains a large amount of reward in the initial phases and the other of which does not. Reward gained on any initial prefix of the agent's life is overshadowed by the long-run average performance. It is possible to generalize this model so that it takes into account both the long run average and the amount of initial reward than can be gained. In the generalized, bias optimal model, a policy is preferred if it maximizes the long-run average and ties are broken by the initial extra reward.
Figure 2 contrasts these models of optimality by providing an environment
in which changing the model of optimality changes the optimal policy. In this
example, circles represent the states of the environment and arrows are state
transitions. There is only a single action choice from every state except the
start state, which is in the upper left and marked with an incoming arrow. All
rewards are zero except where marked. Under a finite-horizon model with h=5,
the three actions yield rewards of +6.0, +0.0, and +0.0, so the first action
should be chosen; under an infinite-horizon discounted model with ![]() =0.9
, the three choices yield +16.2, +59.0, and +58.5 so the second action should
be chosen; and under the average reward model, the third action should be chosen
since it leads to an average reward of +11. If we change h to 1000 and
=0.9
, the three choices yield +16.2, +59.0, and +58.5 so the second action should
be chosen; and under the average reward model, the third action should be chosen
since it leads to an average reward of +11. If we change h to 1000 and
![]() to 0.2, then the second action is
optimal for the finite-horizon model and the first for the infinite-horizon
discounted model; however, the average reward model will always prefer the best
long-term average. Since the choice of optimality model and parameters matters
so much, it is important to choose it carefully in any application.
to 0.2, then the second action is
optimal for the finite-horizon model and the first for the infinite-horizon
discounted model; however, the average reward model will always prefer the best
long-term average. Since the choice of optimality model and parameters matters
so much, it is important to choose it carefully in any application.
The finite-horizon model is appropriate when the agent's lifetime is known; one important aspect of this model is that as the length of the remaining lifetime decreases, the agent's policy may change. A system with a hard deadline would be appropriately modeled this way. The relative usefulness of infinite-horizon discounted and bias-optimal models is still under debate. Bias-optimality has the advantage of not requiring a discount parameter; however, algorithms for finding bias-optimal policies are not yet as well-understood as those for finding optimal infinite-horizon discounted policies.
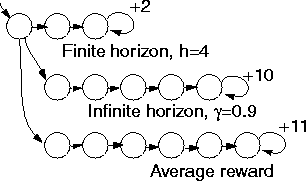
Figure 2: Comparing models of optimality. All unlabeled arrows
produce a reward of zero.
The criteria given in the previous section can be used to assess the policies learned by a given algorithm. We would also like to be able to evaluate the quality of learning itself. There are several incompatible measures in use.
It should be noted that here we have another difference between reinforcement learning and conventional supervised learning. In the latter, expected future predictive accuracy or statistical efficiency are the prime concerns. For example, in the well-known PAC framework [127], there is a learning period during which mistakes do not count, then a performance period during which they do. The framework provides bounds on the necessary length of the learning period in order to have a probabilistic guarantee on the subsequent performance. That is usually an inappropriate view for an agent with a long existence in a complex environment.
In spite of the mismatch between embedded reinforcement learning and the train/test perspective, Fiechter [39] provides a PAC analysis for Q-learning (described in Section 4.2) that sheds some light on the connection between the two views.
Measures related to speed of learning have an additional weakness. An algorithm that merely tries to achieve optimality as fast as possible may incur unnecessarily large penalties during the learning period. A less aggressive strategy taking longer to achieve optimality, but gaining greater total reinforcement during its learning might be preferable.
Adaptive control [19, 112] is also concerned with algorithms for improving a sequence of decisions from experience. Adaptive control is a much more mature discipline that concerns itself with dynamic systems in which states and actions are vectors and system dynamics are smooth: linear or locally linearizable around a desired trajectory. A very common formulation of cost functions in adaptive control are quadratic penalties on deviation from desired state and action vectors. Most importantly, although the dynamic model of the system is not known in advance, and must be estimated from data, the structure of the dynamic model is fixed, leaving model estimation as a parameter estimation problem. These assumptions permit deep, elegant and powerful mathematical analysis, which in turn lead to robust, practical, and widely deployed adaptive control algorithms.
One major difference between reinforcement learning and supervised learning is that a reinforcement-learner must explicitly explore its environment. In order to highlight the problems of exploration, we treat a very simple case in this section. The fundamental issues and approaches described here will, in many cases, transfer to the more complex instances of reinforcement learning discussed later in the paper.
The simplest possible reinforcement-learning problem is known as the k-armed bandit problem, which has been the subject of a great deal of study in the statistics and applied mathematics literature [12]. The agent is in a room with a collection of k gambling machines (each called a "one-armed bandit'' in colloquial English). The agent is permitted a fixed number of pulls, h. Any arm may be pulled on each turn. The machines do not require a deposit to play; the only cost is in wasting a pull playing a suboptimal machine. When arm i is pulled, machine i pays off 1 or 0, according to some underlying probability parameter pi , where payoffs are independent events and the pi s are unknown. What should the agent's strategy be?
This problem illustrates the fundamental tradeoff between exploitation and exploration. The agent might believe that a particular arm has a fairly high payoff probability; should it choose that arm all the time, or should it choose another one that it has less information about, but seems to be worse? Answers to these questions depend on how long the agent is expected to play the game; the longer the game lasts, the worse the consequences of prematurely converging on a sub-optimal arm, and the more the agent should explore.
There is a wide variety of solutions to this problem. We will consider a representative selection of them, but for a deeper discussion and a number of important theoretical results, see the book by Berry and Fristedt [12]. We use the term ``action'' to indicate the agent's choice of arm to pull. This eases the transition into delayed reinforcement models in Section 3. It is very important to note that bandit problems fit our definition of a reinforcement-learning environment with a single state with only self transitions.
Section 2.1 discusses three solutions to the basic one-state bandit problem that have formal correctness results. Although they can be extended to problems with real-valued rewards, they do not apply directly to the general multi-state delayed-reinforcement case. Section 2.2 presents three techniques that are not formally justified, but that have had wide use in practice, and can be applied (with similar lack of guarantee) to the general case.
There is a fairly well-developed formal theory of exploration for very simple problems. Although it is instructive, the methods it provides do not scale well to more complex problems.
If the agent is going to be acting for a total of h steps, it can use basic Bayesian reasoning to solve for an optimal strategy [12]. This requires an assumed prior joint distribution for the parameters {pi} , the most natural of which is that each piis independently uniformly distributed between 0 and 1. We compute a mapping from belief states (summaries of the agent's experiences during this run) to actions. Here, a belief state can be represented as a tabulation of action choices and payoffs: {n1,w1,n2,w2, ... ,nk,wk} denotes a state of play in which each arm i has been pulled ni times with wi payoffs. We write V*(n1,w1, ... ,nk,wk) as the expected payoff remaining, given that a total of h pulls are available, and we use the remaining pulls optimally.
If ![]() , then there
are no remaining pulls, and V*(n1,w1, ... ,nk,wk)
=0. This is the basis of a recursive definition. If we know the V* value
for all belief states with t pulls remaining, we can compute theV*
value of any belief state with t+1 pulls remaining:
, then there
are no remaining pulls, and V*(n1,w1, ... ,nk,wk)
=0. This is the basis of a recursive definition. If we know the V* value
for all belief states with t pulls remaining, we can compute theV*
value of any belief state with t+1 pulls remaining:

where piis the posterior subjective probability of action i paying off given ni , wi and our prior probability. For the uniform priors, which result in a beta distribution, pi=(wi +1)/(ni +2) .
The expense of filling in the table of V* values in this way for all attainable belief states is linear in the number of belief states times actions, and thus exponential in the horizon.
Gittins gives an ``allocation index'' method for finding the optimal choice of action at each step in k-armed bandit problems [40]. The technique only applies under the discounted expected reward criterion. For each action, consider the number of times it has been chosen, n, versus the number of times it has paid off, w. For certain discount factors, there are published tables of ``index values,'' I(n,w) for each pair of n and w. Look up the index value for each action i, I(ni,wi) . It represents a comparative measure of the combined value of the expected payoff of action i (given its history of payoffs) and the value of the information that we would get by choosing it. Gittins has shown that choosing the action with the largest index value guarantees the optimal balance between exploration and exploitation.
Because of the guarantee of optimal exploration and the simplicity of the technique (given the table of index values), this approach holds a great deal of promise for use in more complex applications. This method proved useful in an application to robotic manipulation with immediate reward [98]. Unfortunately, no one has yet been able to find an analog of index values for delayed reinforcement problems.
A branch of the theory of adaptive control is devoted to learning automata, surveyed by Narendra and Thathachar [85], which were originally described explicitly as finite state automata. The Tsetlin automaton shown in Figure 3 provides an example that solves a 2-armed bandit arbitrarily near optimally as N approaches infinity.
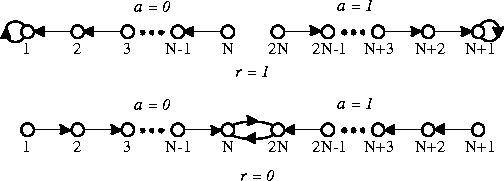
Figure 3: A Tsetlin automaton with 2N states. The
top row shows the state transitions that are made when the previous action
resulted in a reward of 1; the bottom row shows transitions after a reward of 0.
In states in the left half of the figure, action 0 is taken; in those on the
right, action 1 is taken.
It is inconvenient to describe algorithms as finite-state automata, so a move was made to describe the internal state of the agent as a probability distribution according to which actions would be chosen. The probabilities of taking different actions would be adjusted according to their previous successes and failures.
An example, which stands among a set of algorithms independently developed in the mathematical psychology literature [45], is the linear reward-inaction algorithm. Let pi be the agent's probability of taking action i.
![]()
This algorithm converges with probability 1 to a vector containing a single 1
and the rest 0's (choosing a particular action with probability 1).
Unfortunately, it does not always converge to the correct action; but the
probability that it converges to the wrong one can be made arbitrarily small by
making ![]() small [86].
There is no literature on the regret of this algorithm.
small [86].
There is no literature on the regret of this algorithm.
In reinforcement-learning practice, some simple, ad hoc strategies have been popular. They are rarely, if ever, the best choice for the models of optimality we have used, but they may be viewed as reasonable, computationally tractable, heuristics. Thrun [124] has surveyed a variety of these techniques.
The first strategy that comes to mind is to always choose the action with the highest estimated payoff. The flaw is that early unlucky sampling might indicate that the best action's reward is less than the reward obtained from a suboptimal action. The suboptimal action will always be picked, leaving the true optimal action starved of data and its superiority never discovered. An agent must explore to ameliorate this outcome.
A useful heuristic is optimism in the face of uncertainty in which actions are selected greedily, but strongly optimistic prior beliefs are put on their payoffs so that strong negative evidence is needed to eliminate an action from consideration. This still has a measurable danger of starving an optimal but unlucky action, but the risk of this can be made arbitrarily small. Techniques like this have been used in several reinforcement learning algorithms including the interval exploration method [52] (described shortly), the exploration bonus in Dyna [116], curiosity-driven exploration [102], and the exploration mechanism in prioritized sweeping [83].
Another simple exploration strategy is to take the action with the best estimated expected reward by default, but with probability p, choose an action at random. Some versions of this strategy start with a large value of p to encourage initial exploration, which is slowly decreased.
An objection to the simple strategy is that when it experiments with a non-greedy action it is no more likely to try a promising alternative than a clearly hopeless alternative. A slightly more sophisticated strategy is Boltzmann exploration. In this case, the expected reward for taking action a, ER(a) is used to choose an action probabilistically according to the distribution
![]()
The temperature parameter T can be decreased over time to decrease exploration. This method works well if the best action is well separated from the others, but suffers somewhat when the values of the actions are close. It may also converge unnecessarily slowly unless the temperature schedule is manually tuned with great care.
Exploration is often more efficient when it is based on second-order information
about the certainty or variance of the estimated values of actions. Kaelbling's
interval estimation algorithm [52] stores statistics for each
action ![]() : wi is the
number of successes and ni the number of trials. An action
is chosen by computing the upper bound of a 100(1-
: wi is the
number of successes and ni the number of trials. An action
is chosen by computing the upper bound of a 100(1-![]() )%
confidence interval on the success probability of each action and choosing the
action with the highest upper bound. Smaller values of the
)%
confidence interval on the success probability of each action and choosing the
action with the highest upper bound. Smaller values of the ![]() parameter encourage greater exploration.
When payoffs are boolean, the normal approximation to the binomial distribution
can be used to construct the confidence interval (though the binomial should
be used for small n). Other payoff distributions can be handled using
their associated statistics or with nonparametric methods. The method works
very well in empirical trials. It is also related to a certain class of statistical
techniques known as experiment design methods [17], which are
used for comparing multiple treatments (for example, fertilizers or drugs) to
determine which treatment (if any) is best in as small a set of experiments
as possible.
parameter encourage greater exploration.
When payoffs are boolean, the normal approximation to the binomial distribution
can be used to construct the confidence interval (though the binomial should
be used for small n). Other payoff distributions can be handled using
their associated statistics or with nonparametric methods. The method works
very well in empirical trials. It is also related to a certain class of statistical
techniques known as experiment design methods [17], which are
used for comparing multiple treatments (for example, fertilizers or drugs) to
determine which treatment (if any) is best in as small a set of experiments
as possible.
When there are multiple states, but reinforcement is still immediate, then any of the above solutions can be replicated, once for each state. However, when generalization is required, these solutions must be integrated with generalization methods (see section 6); this is straightforward for the simple ad-hoc methods, but it is not understood how to maintain theoretical guarantees.
Many of these techniques focus on converging to some regime in which exploratory actions are taken rarely or never; this is appropriate when the environment is stationary. However, when the environment is non-stationary, exploration must continue to take place, in order to notice changes in the world. Again, the more ad-hoc techniques can be modified to deal with this in a plausible manner (keep temperature parameters from going to 0; decay the statistics in interval estimation), but none of the theoretically guaranteed methods can be applied.
In the general case of the reinforcement learning problem, the agent's actions determine not only its immediate reward, but also (at least probabilistically) the next state of the environment. Such environments can be thought of as networks of bandit problems, but the agent must take into account the next state as well as the immediate reward when it decides which action to take. The model of long-run optimality the agent is using determines exactly how it should take the value of the future into account. The agent will have to be able to learn from delayed reinforcement: it may take a long sequence of actions, receiving insignificant reinforcement, then finally arrive at a state with high reinforcement. The agent must be able to learn which of its actions are desirable based on reward that can take place arbitrarily far in the future.
Problems with delayed reinforcement are well modeled as Markov decision processes (MDPs). An MDP consists of
Although general MDPs may have infinite (even uncountable) state and action spaces, we will only discuss methods for solving finite-state and finite-action problems. In section 6, we discuss methods for solving problems with continuous input and output spaces.
Before we consider algorithms for learning to behave in MDP environments, we will explore techniques for determining the optimal policy given a correct model. These dynamic programming techniques will serve as the foundation and inspiration for the learning algorithms to follow. We restrict our attention mainly to finding optimal policies for the infinite-horizon discounted model, but most of these algorithms have analogs for the finite-horizon and average-case models as well. We rely on the result that, for the infinite-horizon discounted model, there exists an optimal deterministic stationary policy [10].
We will speak of the optimal value of a state--it is the expected
infinite discounted sum of reward that the agent will gain if it starts in that
state and executes the optimal policy. Using ![]() as a
complete decision policy, it is written
as a
complete decision policy, it is written
![]()
This optimal value function is unique and can be defined as the solution to the simultaneous equations
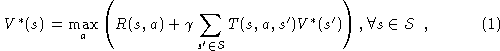
which assert that the value of a state s is the expected instantaneous reward plus the expected discounted value of the next state, using the best available action. Given the optimal value function, we can specify the optimal policy as
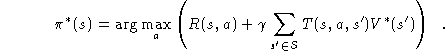
One way, then, to find an optimal policy is to find the optimal value function. It can be determined by a simple iterative algorithm called value iteration that can be shown to converge to the correct V* values [10, 13].
initialize V(s) arbitrarily loop until policy good enough loop forloop for

end loop end loop
It is not obvious when to stop the value iteration algorithm. One important
result bounds the performance of the current greedy policy as a function of the
Bellman residual of the current value function [134].
It says that if the maximum difference between two successive value functions is
less than ![]() , then the value of
the greedy policy, (the policy obtained by choosing, in every state, the action
that maximizes the estimated discounted reward, using the current estimate of
the value function) differs from the value function of the optimal policy by no
more than
, then the value of
the greedy policy, (the policy obtained by choosing, in every state, the action
that maximizes the estimated discounted reward, using the current estimate of
the value function) differs from the value function of the optimal policy by no
more than ![]() at any state. This
provides an effective stopping criterion for the algorithm. Puterman [90]
discusses another stopping criterion, based on the span semi-norm,
which may result in earlier termination. Another important result is that the
greedy policy is guaranteed to be optimal in some finite number of steps even
though the value function may not have converged [13].
And in practice, the greedy policy is often optimal long before the value
function has converged.
at any state. This
provides an effective stopping criterion for the algorithm. Puterman [90]
discusses another stopping criterion, based on the span semi-norm,
which may result in earlier termination. Another important result is that the
greedy policy is guaranteed to be optimal in some finite number of steps even
though the value function may not have converged [13].
And in practice, the greedy policy is often optimal long before the value
function has converged.
Value iteration is very flexible. The assignments to V need not be done in strict order as shown above, but instead can occur asynchronously in parallel provided that the value of every state gets updated infinitely often on an infinite run. These issues are treated extensively by Bertsekas [16], who also proves convergence results.
Updates based on Equation 1 are known as full backups since they make use of information from all possible successor states. It can be shown that updates of the form
![]()
can also be used as long as each pairing of a and s is updated
infinitely often, s' is sampled from the distribution
T(s,a,s'), r is sampled with mean
R(s,a) and bounded variance, and the learning rate ![]() is decreased slowly. This type of sample
backup [111]
is critical to the operation of the model-free methods discussed in the next
section.
is decreased slowly. This type of sample
backup [111]
is critical to the operation of the model-free methods discussed in the next
section.
The computational complexity of the value-iteration algorithm with full backups,
per iteration, is quadratic in the number of states and linear in the number
of actions. Commonly, the transition probabilities T(s,a,s')
are sparse. If there are on average a constant number of next states with non-zero
probability then the cost per iteration is linear in the number of states and
linear in the number of actions. The number of iterations required to reach
the optimal value function is polynomial in the number of states and the magnitude
of the largest reward if the discount factor is held constant. However, in the
worst case the number of iterations grows polynomially in1/(1-![]() ),
so the convergence rate slows considerably as the discount factor approaches
1 [66].
),
so the convergence rate slows considerably as the discount factor approaches
1 [66].
The policy iteration algorithm manipulates the policy directly, rather than finding it indirectly via the optimal value function. It operates as follows:
choose an arbitrary policyloop
compute the value function of policy
: solve the linear equations
improve the policy at each state:
until
The value function of a policy is just the expected infinite discounted reward that will be gained, at each state, by executing that policy. It can be determined by solving a set of linear equations. Once we know the value of each state under the current policy, we consider whether the value could be improved by changing the first action taken. If it can, we change the policy to take the new action whenever it is in that situation. This step is guaranteed to strictly improve the performance of the policy. When no improvements are possible, then the policy is guaranteed to be optimal.
Since there are at most ![]() distinct policies,
and the sequence of policies improves at each step, this algorithm terminates in
at most an exponential number of iterations [90].
However, it is an important open question how many iterations policy iteration
takes in the worst case. It is known that the running time is pseudopolynomial
and that for any fixed discount factor, there is a polynomial bound in the total
size of the MDP [66].
distinct policies,
and the sequence of policies improves at each step, this algorithm terminates in
at most an exponential number of iterations [90].
However, it is an important open question how many iterations policy iteration
takes in the worst case. It is known that the running time is pseudopolynomial
and that for any fixed discount factor, there is a polynomial bound in the total
size of the MDP [66].
In practice, value iteration is much faster per iteration, but policy
iteration takes fewer iterations. Arguments have been put forth to the effect
that each approach is better for large problems. Puterman's modified policy
iteration algorithm [91]
provides a method for trading iteration time for iteration improvement in a
smoother way. The basic idea is that the expensive part of policy iteration is
solving for the exact value of ![]() . Instead of finding an exact value for
. Instead of finding an exact value for ![]() , we can perform a few steps of a modified
value-iteration step where the policy is held fixed over successive iterations.
This can be shown to produce an approximation to
, we can perform a few steps of a modified
value-iteration step where the policy is held fixed over successive iterations.
This can be shown to produce an approximation to ![]() that converges linearly in
that converges linearly in ![]() . In practice, this can result in substantial speedups.
. In practice, this can result in substantial speedups.
Several standard numerical-analysis techniques that speed the convergence of dynamic programming can be used to accelerate value and policy iteration. Multigrid methods can be used to quickly seed a good initial approximation to a high resolution value function by initially performing value iteration at a coarser resolution [93]. State aggregation works by collapsing groups of states to a single meta-state solving the abstracted problem [15].
Value iteration works by producing successive approximations of the optimal
value function. Each iteration can be performed in ![]() steps, or faster if there is sparsity in the transition
function. However, the number of iterations required can grow exponentially in
the discount factor [27];
as the discount factor approaches 1, the decisions must be based on results that
happen farther and farther into the future. In practice, policy iteration
converges in fewer iterations than value iteration, although the per-iteration
costs of
steps, or faster if there is sparsity in the transition
function. However, the number of iterations required can grow exponentially in
the discount factor [27];
as the discount factor approaches 1, the decisions must be based on results that
happen farther and farther into the future. In practice, policy iteration
converges in fewer iterations than value iteration, although the per-iteration
costs of ![]() can be
prohibitive. There is no known tight worst-case bound available for policy
iteration [66].
Modified policy iteration [91]
seeks a trade-off between cheap and effective iterations and is preferred by
some practictioners [96].
can be
prohibitive. There is no known tight worst-case bound available for policy
iteration [66].
Modified policy iteration [91]
seeks a trade-off between cheap and effective iterations and is preferred by
some practictioners [96].
Linear programming [105] is an extremely general problem, and MDPs can be solved by general-purpose linear-programming packages [35, 34, 46]. An advantage of this approach is that commercial-quality linear-programming packages are available, although the time and space requirements can still be quite high. From a theoretic perspective, linear programming is the only known algorithm that can solve MDPs in polynomial time, although the theoretically efficient algorithms have not been shown to be efficient in practice.
In the previous section we reviewed methods for obtaining an optimal policy for an MDP assuming that we already had a model. The model consists of knowledge of the state transition probability function T(s,a,s') and the reinforcement function R(s,a). Reinforcement learning is primarily concerned with how to obtain the optimal policy when such a model is not known in advance. The agent must interact with its environment directly to obtain information which, by means of an appropriate algorithm, can be processed to produce an optimal policy.
At this point, there are two ways to proceed.
This section examines model-free learning, and Section 5 examines model-based methods.
The biggest problem facing a reinforcement-learning agent is temporal credit assignment. How do we know whether the action just taken is a good one, when it might have far-reaching effects? One strategy is to wait until the ``end'' and reward the actions taken if the result was good and punish them if the result was bad. In ongoing tasks, it is difficult to know what the ``end'' is, and this might require a great deal of memory. Instead, we will use insights from value iteration to adjust the estimated value of a state based on the immediate reward and the estimated value of the next state. This class of algorithms is known as temporal difference methods [115]. We will consider two different temporal-difference learning strategies for the discounted infinite-horizon model.
The adaptive heuristic critic algorithm is an adaptive version of policy iteration [9] in which the value-function computation is no longer implemented by solving a set of linear equations, but is instead computed by an algorithm called TD(0). A block diagram for this approach is given in Figure 4. It consists of two components: a critic (labeled AHC), and a reinforcement-learning component (labeled RL). The reinforcement-learning component can be an instance of any of the k-armed bandit algorithms, modified to deal with multiple states and non-stationary rewards. But instead of acting to maximize instantaneous reward, it will be acting to maximize the heuristic value, v, that is computed by the critic. The critic uses the real external reinforcement signal to learn to map states to their expected discounted values given that the policy being executed is the one currently instantiated in the RL component.

Figure 4: Architecture for the
adaptive heuristic critic.
We can see the analogy with modified policy iteration if we imagine these components
working in alternation. The policy ![]() implemented by RL is fixed and the
critic learns the value function
implemented by RL is fixed and the
critic learns the value function ![]() for that policy. Now we fix the critic and let the RL component
learn a new policy
for that policy. Now we fix the critic and let the RL component
learn a new policy ![]() that maximizes the new value function, and so on. In most
implementations, however, both components operate simultaneously. Only the alternating
implementation can be guaranteed to converge to the optimal policy, under appropriate
conditions. Williams and Baird explored the convergence properties of a class
of AHC-related algorithms they call "incremental variants of policy iteration'' [133].
that maximizes the new value function, and so on. In most
implementations, however, both components operate simultaneously. Only the alternating
implementation can be guaranteed to converge to the optimal policy, under appropriate
conditions. Williams and Baird explored the convergence properties of a class
of AHC-related algorithms they call "incremental variants of policy iteration'' [133].
It remains to explain how the critic can learn the value of a policy. We
define ![]() to be an experience tuple summarizing a single
transition in the environment. Here s is the agent's state before the
transition, a is its choice of action, r the instantaneous reward
it receives, and s' its resulting state. The value of a policy is learned
using Sutton's TD(0) algorithm [115]
which uses the update rule
to be an experience tuple summarizing a single
transition in the environment. Here s is the agent's state before the
transition, a is its choice of action, r the instantaneous reward
it receives, and s' its resulting state. The value of a policy is learned
using Sutton's TD(0) algorithm [115]
which uses the update rule
![]()
Whenever a state s is visited, its estimated value is updated to be
closer to r+![]() V(s')
, since r is the instantaneous reward received and V(s')
is the estimated value of the actually occurring next state. This is analogous
to the sample-backup rule from value iteration--the only difference is that
the sample is drawn from the real world rather than by simulating a known model.
The key idea is that r+
V(s')
, since r is the instantaneous reward received and V(s')
is the estimated value of the actually occurring next state. This is analogous
to the sample-backup rule from value iteration--the only difference is that
the sample is drawn from the real world rather than by simulating a known model.
The key idea is that r+![]() V(s')
is a sample of the value of V(s), and it is more likely to be
correct because it incorporates the real r. If the learning rate
V(s')
is a sample of the value of V(s), and it is more likely to be
correct because it incorporates the real r. If the learning rate ![]() is adjusted properly (it must be slowly decreased) and the
policy is held fixed, TD(0) is guaranteed to converge to the optimal
value function.
is adjusted properly (it must be slowly decreased) and the
policy is held fixed, TD(0) is guaranteed to converge to the optimal
value function.
The TD(0) rule as presented above is really an instance of a more general
class of algorithms called ![]() , with
, with ![]() =0.
TD(0) looks only one step ahead when adjusting value estimates; although
it will eventually arrive at the correct answer, it can take quite a while to
do so. The general
=0.
TD(0) looks only one step ahead when adjusting value estimates; although
it will eventually arrive at the correct answer, it can take quite a while to
do so. The general ![]() rule is similar to the TD(0) rule given above,
rule is similar to the TD(0) rule given above,
![]()
but it is applied to every state according to its eligibility e(u), rather than just to the immediately previous state, s. One version of the eligibility trace is defined to be
![]()
The eligibility of a state s is the degree to which it has been visited
in the recent past; when a reinforcement is received, it is used to update all
the states that have been recently visited, according to their eligibility.
When ![]() =0 this is equivalent
to TD(0). When
=0 this is equivalent
to TD(0). When ![]() =1 ,
it is roughly equivalent to updating all the states according to the number
of times they were visited by the end of a run. Note that we can update the
eligibility online as follows:
=1 ,
it is roughly equivalent to updating all the states according to the number
of times they were visited by the end of a run. Note that we can update the
eligibility online as follows:
![]()
It is computationally more expensive to execute the general ![]() , though it often converges considerably faster for large
, though it often converges considerably faster for large
![]() [30, 32].
There has been some recent work on making the updates more efficient [24]
and on changing the definition to make
[30, 32].
There has been some recent work on making the updates more efficient [24]
and on changing the definition to make ![]() more consistent with the certainty-equivalent
method [108],
which is discussed in Section 5.1.
more consistent with the certainty-equivalent
method [108],
which is discussed in Section 5.1.
The work of the two components of AHC can be accomplished in a unified manner
by Watkins' Q-learning algorithm [128, 129]. Q-learning is typically easier
to implement. In order to understand Q-learning, we have to develop some additional
notation. Let Q*(s,a) be the expected discounted reinforcement of taking
action a in state s, then continuing by choosing actions optimally.
Note that V*(s) is the value of s assuming the best action is
taken initially, and so ![]() .Q*(s,a) can hence be written recursively as
.Q*(s,a) can hence be written recursively as
![]()
Note also that, since ![]() , we have
, we have ![]() as an optimal policy.
as an optimal policy.
Because the Q function makes the action explicit, we can estimate the Q values on-line using a method essentially the same as TD(0), but also use them to define the policy, because an action can be chosen just by taking the one with the maximum Q value for the current state.
The Q-learning rule is
![]()
where ![]() is an experience
tuple as described earlier. If each action is executed in each state an infinite
number of times on an infinite run and
is an experience
tuple as described earlier. If each action is executed in each state an infinite
number of times on an infinite run and ![]() is decayed appropriately, the Q values will converge with
probability 1 to Q* [128, 125, 49]. Q-learning can also be extended
to update states that occurred more than one step previously, as in
is decayed appropriately, the Q values will converge with
probability 1 to Q* [128, 125, 49]. Q-learning can also be extended
to update states that occurred more than one step previously, as in ![]() [88].
[88].
When the Q values are nearly converged to their optimal values, it is appropriate for the agent to act greedily, taking, in each situation, the action with the highest Q value. During learning, however, there is a difficult exploitation versus exploration trade-off to be made. There are no good, formally justified approaches to this problem in the general case; standard practice is to adopt one of the ad hoc methods discussed in section 2.2.
AHC architectures seem to be more difficult to work with than Q-learning on a practical level. It can be hard to get the relative learning rates right in AHC so that the two components converge together. In addition, Q-learning is exploration insensitive: that is, that the Q values will converge to the optimal values, independent of how the agent behaves while the data is being collected (as long as all state-action pairs are tried often enough). This means that, although the exploration-exploitation issue must be addressed in Q-learning, the details of the exploration strategy will not affect the convergence of the learning algorithm. For these reasons, Q-learning is the most popular and seems to be the most effective model-free algorithm for learning from delayed reinforcement. It does not, however, address any of the issues involved in generalizing over large state and/or action spaces. In addition, it may converge quite slowly to a good policy.
As described, Q-learning can be applied to discounted infinite-horizon MDPs. It can also be applied to undiscounted problems as long as the optimal policy is guaranteed to reach a reward-free absorbing state and the state is periodically reset.
Schwartz [106] examined the problem of adapting Q-learning to an average-reward framework. Although his R-learning algorithm seems to exhibit convergence problems for some MDPs, several researchers have found the average-reward criterion closer to the true problem they wish to solve than a discounted criterion and therefore prefer R-learning to Q-learning [69].
With that in mind, researchers have studied the problem of learning optimal average-reward policies. Mahadevan [70] surveyed model-based average-reward algorithms from a reinforcement-learning perspective and found several difficulties with existing algorithms. In particular, he showed that existing reinforcement-learning algorithms for average reward (and some dynamic programming algorithms) do not always produce bias-optimal policies. Jaakkola, Jordan and Singh [50] described an average-reward learning algorithm with guaranteed convergence properties. It uses a Monte-Carlo component to estimate the expected future reward for each state as the agent moves through the environment. In addition, Bertsekas presents a Q-learning-like algorithm for average-case reward in his new textbook [14]. Although this recent work provides a much needed theoretical foundation to this area of reinforcement learning, many important problems remain unsolved.
The previous section showed how it is possible to learn an optimal policy without knowing the models T(s,a,s') or R(s,a) and without even learning those models en route. Although many of these methods are guaranteed to find optimal policies eventually and use very little computation time per experience, they make extremely inefficient use of the data they gather and therefore often require a great deal of experience to achieve good performance. In this section we still begin by assuming that we don't know the models in advance, but we examine algorithms that do operate by learning these models. These algorithms are especially important in applications in which computation is considered to be cheap and real-world experience costly.
We begin with the most conceptually straightforward method: first, learn the T and R functions by exploring the environment and keeping statistics about the results of each action; next, compute an optimal policy using one of the methods of Section 3. This method is known as certainty equivlance [57].
There are some serious objections to this method:

Figure: In this environment, due to Whitehead [130], random
exploration would take take O(2n) steps to reach the goal
even once, whereas a more intelligent exploration strategy (e.g. "assume
any untried action leads directly to goal'') would require only O(n2)
steps.
A variation on this idea is certainty equivalence, in which the model is learned continually through the agent's lifetime and, at each step, the current model is used to compute an optimal policy and value function. This method makes very effective use of available data, but still ignores the question of exploration and is extremely computationally demanding, even for fairly small state spaces. Fortunately, there are a number of other model-based algorithms that are more practical.
Sutton's Dyna architecture [116, 117]
exploits a middle ground, yielding strategies that are both more effective than
model-free learning and more computationally efficient than the
certainty-equivalence approach. It simultaneously uses experience to build a
model ( ![]() and
and ![]() ), uses experience to adjust
the policy, and uses the model to adjust the policy.
), uses experience to adjust
the policy, and uses the model to adjust the policy.
Dyna operates in a loop of interaction with the environment. Given an
experience tuple ![]() , it behaves as follows:
, it behaves as follows:
![]()
which is a version of the value-iteration update for Q values.
![]()
The Dyna algorithm requires about k times the computation of Q-learning per instance, but this is typically vastly less than for the naive model-based method. A reasonable value of k can be determined based on the relative speeds of computation and of taking action.
Figure 6 shows a grid world in which in each cell the agent has four actions (N, S, E, W) and transitions are made deterministically to an adjacent cell, unless there is a block, in which case no movement occurs. As we will see in Table 1, Dyna requires an order of magnitude fewer steps of experience than does Q-learning to arrive at an optimal policy. Dyna requires about six times more computational effort, however.

Figure 6: A 3277-state grid world. This was formulated as a
shortest-path reinforcement-learning problem, which yields the same result as
if a reward of 1 is given at the goal, a reward of zero elsewhere and a discount
factor is used.
| Steps before | Backups before | |
| convergence | convergence | |
| Q-learning | 531,000 | 531,000 |
| Dyna | 62,000 | 3,055,000 |
| prioritized sweeping | 28,000 | 1,010,000 |
Although Dyna is a great improvement on previous methods, it suffers from being relatively undirected. It is particularly unhelpful when the goal has just been reached or when the agent is stuck in a dead end; it continues to update random state-action pairs, rather than concentrating on the ``interesting'' parts of the state space. These problems are addressed by prioritized sweeping [83] and Queue-Dyna [87], which are two independently-developed but very similar techniques. We will describe prioritized sweeping in some detail.
The algorithm is similar to Dyna, except that updates are no longer chosen at random and values are now associated with states (as in value iteration) instead of state-action pairs (as in Q-learning). To make appropriate choices, we must store additional information in the model. Each state remembers its predecessors: the states that have a non-zero transition probability to it under some action. In addition, each state has a priority, initially set to zero.
Instead of updating k random state-action pairs, prioritized sweeping updates k states with the highest priority. For each high-priority state s, it works as follows:
![]()
If we have updated the V value for state s' and it has changed
by amount ![]() ,
then the immediate predecessors of s' are informed of this event. Any
state s for which there exists an action a such that
,
then the immediate predecessors of s' are informed of this event. Any
state s for which there exists an action a such that ![]() has its priority promoted to
has its priority promoted to ![]() ,
unless its priority already exceeded that value.
,
unless its priority already exceeded that value.
The global behavior of this algorithm is that when a real-world transition is ``surprising'' (the agent happens upon a goal state, for instance), then lots of computation is directed to propagate this new information back to relevant predecessor states. When the real-world transition is ``boring'' (the actual result is very similar to the predicted result), then computation continues in the most deserving part of the space.
Running prioritized sweeping on the problem in Figure 6, we see a large improvement over Dyna. The optimal policy is reached in about half the number of steps of experience and one-third the computation as Dyna required (and therefore about 20 times fewer steps and twice the computational effort of Q-learning).
Methods proposed for solving MDPs given a model can be used in the context of model-based methods as well.
RTDP (real-time dynamic programming) [8] is another model-based method that uses Q-learning to concentrate computational effort on the areas of the state-space that the agent is most likely to occupy. It is specific to problems in which the agent is trying to achieve a particular goal state and the reward everywhere else is 0. By taking into account the start state, it can find a short path from the start to the goal, without necessarily visiting the rest of the state space.
The Plexus planning system [33, 55] exploits a similar intuition. It starts by making an approximate version of the MDP which is much smaller than the original one. The approximate MDP contains a set of states, called the envelope, that includes the agent's current state and the goal state, if there is one. States that are not in the envelope are summarized by a single "out'' state. The planning process is an alternation between finding an optimal policy on the approximate MDP and adding useful states to the envelope. Action may take place in parallel with planning, in which case irrelevant states are also pruned out of the envelope.
All of the previous discussion has tacitly assumed that it is possible to enumerate the state and action spaces and store tables of values over them. Except in very small environments, this means impractical memory requirements. It also makes inefficient use of experience. In a large, smooth state space we generally expect similar states to have similar values and similar optimal actions. Surely, therefore, there should be some more compact representation than a table. Most problems will have continuous or large discrete state spaces; some will have large or continuous action spaces. The problem of learning in large spaces is addressed through generalization techniques, which allow compact storage of learned information and transfer of knowledge between ``similar'' states and actions.
The large literature of generalization techniques from inductive concept learning can be applied to reinforcement learning. However, techniques often need to be tailored to specific details of the problem. In the following sections, we explore the application of standard function-approximation techniques, adaptive resolution models, and hierarchical methods to the problem of reinforcement learning.
The reinforcement-learning architectures and algorithms discussed above have
included the storage of a variety of mappings, including ![]() (policies),
(policies), ![]() (value functions),
(value functions),
![]() (Q functions and rewards),
(Q functions and rewards), ![]() (deterministic transitions), and
(deterministic transitions), and ![]() (transition probabilities). Some of these mappings, such as
transitions and immediate rewards, can be learned using straightforward
supervised learning, and can be handled using any of the wide variety of
function-approximation techniques for supervised learning that support noisy
training examples. Popular techniques include various neural-network
methods [94], fuzzy logic [11, 58].
CMAC [3], and local memory-based methods [84],
such as generalizations of nearest neighbor methods. Other mappings, especially
the policy mapping, typically need specialized algorithms because training sets
of input-output pairs are not available.
(transition probabilities). Some of these mappings, such as
transitions and immediate rewards, can be learned using straightforward
supervised learning, and can be handled using any of the wide variety of
function-approximation techniques for supervised learning that support noisy
training examples. Popular techniques include various neural-network
methods [94], fuzzy logic [11, 58].
CMAC [3], and local memory-based methods [84],
such as generalizations of nearest neighbor methods. Other mappings, especially
the policy mapping, typically need specialized algorithms because training sets
of input-output pairs are not available.
When the agent's actions do not influence state transitions, the resulting problem becomes one of choosing actions to maximize immediate reward as a function of the agent's current state. These problems bear a resemblance to the bandit problems discussed in Section 2 except that the agent should condition its action selection on the current state. For this reason, this class of problems has been described as associative reinforcement learning.
The algorithms in this section address the problem of learning from immediate boolean reinforcement where the state is vector valued and the action is a boolean vector. Such algorithms can and have been used in the context of a delayed reinforcement, for instance, as the RL component in the AHC architecture described in Section 4.1. They can also be generalized to real-valued reward through reward comparison methods [114].
The idea behind this training rule is that whenever an action fails to generate reward, CRBP will try to generate an action that is different from the current choice. Although it seems like the algorithm might oscillate between an action and its complement, that does not happen. One step of training a network will only change the action slightly and since the output probabilities will tend to move toward 0.5, this makes action selection more random and increases search. The hope is that the random distribution will generate an action that works better, and then that action will be reinforced.
In the simplest case, the entire system learns only to optimize immediate reward. First, let us consider the behavior of the network that learns the policy, a mapping from a vector describing s to a 0 or 1. If the output unit has activation yi , then a, the action generated, will be 1 if y+v>0 , where v is normal noise, and 0 otherwise.
The adjustment for the output unit is, in the simplest case,
![]()
where the first factor is the reward received for taking the most recent action and the second encodes which action was taken. The actions are encoded as 0 and 1, so a - 1/2 always has the same magnitude; if the reward and the action have the same sign, then action 1 will be made more likely, otherwise action 0 will be.
As described, the network will tend to seek actions that given positive reward. To extend this approach to maximize reward, we can compare the reward to some baseline, b. This changes the adjustment to
![]()
where b is the output of the second network. The second network is trained in a standard supervised mode to estimate r as a function of the input state s.
Variations of this approach have been used in a variety of applications [4, 9, 61, 114].
Williams [131, 132] studied the problem of choosing actions to maximize immedate reward. He identified a broad class of update rules that perform gradient descent on the expected reward and showed how to integrate these rules with backpropagation. This class, called REINFORCE algorithms, includes linear reward-inaction (Section 2.1.3) as a special case.
The generic REINFORCE update for a parameter wij can be written
![]()
where ![]() is a non-negative
factor, r the current reinforcement, bij a reinforcement
baseline, and gi is the probability density function used
to randomly generate actions based on unit activations. Both
is a non-negative
factor, r the current reinforcement, bij a reinforcement
baseline, and gi is the probability density function used
to randomly generate actions based on unit activations. Both ![]() and bij can take on different values
for each wij, however, when
and bij can take on different values
for each wij, however, when ![]() is constant throughout the system, the expected update is exactly in the direction
of the expected reward gradient. Otherwise, the update is in the same half space
as the gradient but not necessarily in the direction of steepest increase.
is constant throughout the system, the expected update is exactly in the direction
of the expected reward gradient. Otherwise, the update is in the same half space
as the gradient but not necessarily in the direction of steepest increase.
Williams points out that the choice of baseline, bij, can have a profound effect on the convergence speed of the algorithm.
The restriction to a single boolean output makes these techniques difficult to apply. In very benign learning situations, it is possible to extend this approach to use a collection of learners to independently learn the individual bits that make up a complex output. In general, however, that approach suffers from the problem of very unreliable reinforcement: if a single learner generates an inappropriate output bit, all of the learners receive a low reinforcement value. The CASCADE method [52] allows a collection of learners to be trained collectively to generate appropriate joint outputs; it is considerably more reliable, but can require additional computational effort.
Another method to allow reinforcement-learning techniques to be applied in large state spaces is modeled on value iteration and Q-learning. Here, a function approximator is used to represent the value function by mapping a state description to a value.
Many reseachers have experimented with this approach: Boyan and Moore [18]
used local memory-based methods in conjunction with value iteration; Lin [59]
used backpropagation networks for Q-learning; Watkins [128] used CMAC for
Q-learning; Tesauro [118, 120] used backpropagation for learning the value
function in backgammon (described in Section 8.1); Zhang and Dietterich [136]
used backpropagation and ![]() to learn good strategies
for job-shop scheduling.
to learn good strategies
for job-shop scheduling.
Although there have been some positive examples, in general there are unfortunate interactions between function approximation and the learning rules. In discrete environments there is a guarantee that any operation that updates the value function (according to the Bellman equations) can only reduce the error between the current value function and the optimal value function. This guarantee no longer holds when generalization is used. These issues are discussed by Boyan and Moore [18], who give some simple examples of value function errors growing arbitrarily large when generalization is used with value iteration. Their solution to this, applicable only to certain classes of problems, discourages such divergence by only permitting updates whose estimated values can be shown to be near-optimal via a battery of Monte-Carlo experiments.
Thrun and Schwartz [123] theorize that function approximation of value functions is also dangerous because the errors in value functions due to generalization can become compounded by the ``max'' operator in the definition of the value function.
Several recent results [42, 126] show how the appropriate choice of function approximator can guarantee convergence, though not necessarily to the optimal values. Baird's residual gradient technique [6] provides guaranteed convergence to locally optimal solutions.
Perhaps the gloominess of these counter-examples is misplaced. Boyan and Moore [18] report that their counter-examples can be made to work with problem-specific hand-tuning despite the unreliability of untuned algorithms that provably converge in discrete domains. Sutton [113] shows how modified versions of Boyan and Moore's examples can converge successfully. An open question is whether general principles, ideally supported by theory, can help us understand when value function approximation will succeed. In Sutton's comparative experiments with Boyan and Moore's counter-examples, he changes four aspects of the experiments:
The networks described in Section 6.1.1 generalize over state descriptions presented as inputs. They also produce outputs in a discrete, factored representation and thus could be seen as generalizing over actions as well.
In cases such as this when actions are described combinatorially, it is important to generalize over actions to avoid keeping separate statistics for the huge number of actions that can be chosen. In continuous action spaces, the need for generalization is even more pronounced.
When estimating Q values using a neural network, it is possible to use either a distinct network for each action, or a network with a distinct output for each action. When the action space is continuous, neither approach is possible. An alternative strategy is to use a single network with both the state and action as input and Q value as the output. Training such a network is not conceptually difficult, but using the network to find the optimal action can be a challenge. One method is to do a local gradient-ascent search on the action in order to find one with high value [7].
Gullapalli [43, 44] has developed a ``neural'' reinforcement-learning unit for use in continuous action spaces. The unit generates actions with a normal distribution; it adjusts the mean and variance based on previous experience. When the chosen actions are not performing well, the variance is high, resulting in exploration of the range of choices. When an action performs well, the mean is moved in that direction and the variance decreased, resulting in a tendency to generate more action values near the successful one. This method was successfully employed to learn to control a robot arm with many continuous degrees of freedom.
Another strategy for dealing with large state spaces is to treat them as a hierarchy of learning problems. In many cases, hierarchical solutions introduce slight sub-optimality in performance, but potentially gain a good deal of efficiency in execution time, learning time, and space.
Hierarchical learners are commonly structured as gated behaviors, as shown in Figure 8. There is a collection of behaviors that map environment states into low-level actions and a gating function that decides, based on the state of the environment, which behavior's actions should be switched through and actually executed. Maes and Brooks [68] used a version of this architecture in which the individual behaviors were fixed a priori and the gating function was learned from reinforcement. Mahadevan and Connell [72] used the dual approach: they fixed the gating function, and supplied reinforcement functions for the individual behaviors, which were learned. Lin [60] and Dorigo and Colombetti [38, 37] both used this approach, first training the behaviors and then training the gating function. Many of the other hierarchical learning methods can be cast in this framework.
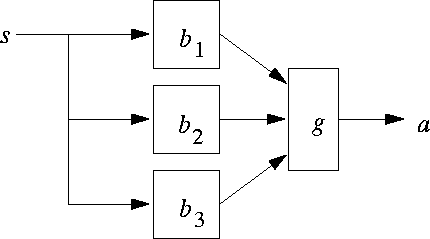
Figure 8: A structure of gated behaviors.
Feudal Q-learning [31, 128] involves a hierarchy of learning modules. In the simplest case, there is a high-level master and a low-level slave. The master receives reinforcement from the external environment. Its actions consist of commands that it can give to the low-level learner. When the master generates a particular command to the slave, it must reward the slave for taking actions that satisfy the command, even if they do not result in external reinforcement. The master, then, learns a mapping from states to commands. The slave learns a mapping from commands and states to external actions. The set of ``commands'' and their associated reinforcement functions are established in advance of the learning.
This is really an instance of the general ``gated behaviors'' approach, in which the slave can execute any of the behaviors depending on its command. The reinforcement functions for the individual behaviors (commands) are given, but learning takes place simultaneously at both the high and low levels.
Singh's compositional Q-learning [110, 109] (C-QL) consists of a hierarchy based on the temporal sequencing of subgoals. The elemental tasks are behaviors that achieve some recognizable condition. The high-level goal of the system is to achieve some set of conditions in sequential order. The achievement of the conditions provides reinforcement for the elemental tasks, which are trained first to achieve individual subgoals. Then, the gating function learns to switch the elemental tasks in order to achieve the appropriate high-level sequential goal. This method was used by Tham and Prager [121] to learn to control a simulated multi-link robot arm.
Especially if we consider reinforcement learning modules to be part of larger agent architectures, it is important to consider problems in which goals are dynamically input to the learner. Kaelbling's HDG algorithm [51] uses a hierarchical approach to solving problems when goals of achievement (the agent should get to a particular state as quickly as possible) are given to an agent dynamically.
The HDG algorithm works by analogy with navigation in a harbor. The environment is partitioned (a priori, but more recent work [5] addresses the case of learning the partition) into a set of regions whose centers are known as ``landmarks.'' If the agent is currently in the same region as the goal, then it uses low-level actions to move to the goal. If not, then high-level information is used to determine the next landmark on the shortest path from the agent's closest landmark to the goal's closest landmark. Then, the agent uses low-level information to aim toward that next landmark. If errors in action cause deviations in the path, there is no problem; the best aiming point is recomputed on every step.
In many real-world environments, it will not be possible for the agent to have perfect and complete perception of the state of the environment. Unfortunately, complete observability is necessary for learning methods based on MDPs. In this section, we consider the case in which the agent makes observations of the state of the environment, but these observations may be noisy and provide incomplete information. In the case of a robot, for instance, it might observe whether it is in a corridor, an open room, a T-junction, etc., and those observations might be error-prone. This problem is also referred to as the problem of ``incomplete perception,'' ``perceptual aliasing,'' or ``hidden state.''
In this section, we will consider extensions to the basic MDP framework for solving partially observable problems. The resulting formal model is called a partially observable Markov decision process or POMDP.
The most naive strategy for dealing with partial observability is to ignore it. That is, to treat the observations as if they were the states of the environment and try to learn to behave. Figure 9 shows a simple environment in which the agent is attempting to get to the printer from an office. If it moves from the office, there is a good chance that the agent will end up in one of two places that look like ``hall'', but that require different actions for getting to the printer. If we consider these states to be the same, then the agent cannot possibly behave optimally. But how well can it do?

Figure 9: An example of a partially observable
environment.
The resulting problem is not Markovian, and Q-learning cannot be guaranteed to converge. Small breaches of the Markov requirement are well handled by Q-learning, but it is possible to construct simple environments that cause Q-learning to oscillate [23]. It is possible to use a model-based approach, however; act according to some policy and gather statistics about the transitions between observations, then solve for the optimal policy based on those observations. Unfortunately, when the environment is not Markovian, the transition probabilities depend on the policy being executed, so this new policy will induce a new set of transition probabilities. This approach may yield plausible results in some cases, but again, there are no guarantees.
It is reasonable, though, to ask what the optimal policy (mapping from observations to actions, in this case) is. It is NP-hard [64] to find this mapping, and even the best mapping can have very poor performance. In the case of our agent trying to get to the printer, for instance, any deterministic state-free policy takes an infinite number of steps to reach the goal on average.
Some improvement can be gained by considering stochastic policies; these are mappings from observations to probability distributions over actions. If there is randomness in the agent's actions, it will not get stuck in the hall forever. Jaakkola, Singh, and Jordan [50] have developed an algorithm for finding locally-optimal stochastic policies, but finding a globally optimal policy is still NP hard.
In our example, it turns out that the optimal stochastic policy is for the
agent, when in a state that looks like a hall, to go east with probability ![]() and
west with probability
and
west with probability ![]() .
This policy can be found by solving a simple (in this case) quadratic program.
The fact that such a simple example can produce irrational numbers gives some
indication that it is a difficult problem to solve exactly.
.
This policy can be found by solving a simple (in this case) quadratic program.
The fact that such a simple example can produce irrational numbers gives some
indication that it is a difficult problem to solve exactly.
The only way to behave truly effectively in a wide-range of environments is to use memory of previous actions and observations to disambiguate the current state. There are a variety of approaches to learning policies with internal state.
Recently, this approach has been reexamined using insights from the reinforcement-learning literature, with some success. Dorigo did a comparative study of Q-learning and classifier systems [36]. Cliff and Ross [26] start with Wilson's zeroth-level classifier system [135] and add one and two-bit memory registers. They find that, although their system can learn to use short-term memory registers effectively, the approach is unlikely to scale to more complex environments.
Dorigo and Colombetti applied classifier systems to a moderately complex problem of learning robot behavior from immediate reinforcement [38, 37].
Chrisman [22] showed how the forward-backward algorithm for learning HMMs could be adapted to learning POMDPs. He, and later McCallum [75], also gave heuristic state-splitting rules to attempt to learn the smallest possible model for a given environment. The resulting model can then be used to integrate information from the agent's observations in order to make decisions.
Figure 10 illustrates the basic structure for a perfect-memory controller.
The component on the left is the state estimator, which computes the
agent's belief state, b as a function of the old belief state,
the last action a, and the current observation i. In this context,
a belief state is a probability distribution over states of the environment,
indicating the likelihood, given the agent's past experience, that the environment
is actually in each of those states. The state estimator can be constructed
straightforwardly using the estimated world model and Bayes' rule.
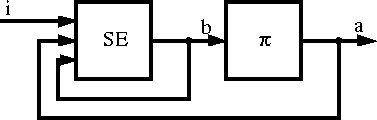
Figure
10: Structure of a POMDP agent.
Now we are left with the problem of finding a policy mapping belief states into action. This problem can be formulated as an MDP, but it is difficult to solve using the techniques described earlier, because the input space is continuous. Chrisman's approach [22] does not take into account future uncertainty, but yields a policy after a small amount of computation. A standard approach from the operations-research literature is to solve for the optimal policy (or a close approximation thereof) based on its representation as a piecewise-linear and convex function over the belief space. This method is computationally intractable, but may serve as inspiration for methods that make further approximations [20, 65].
Practical applications provide a test of the efficacy and usefulness of learning algorithms. They are also an inspiration for deciding which components of the reinforcement learning framework are of practical importance. For example, a researcher with a real robotic task can provide a data point to questions such as:
Game playing has dominated the Artificial Intelligence world as a problem domain ever since the field was born. Two-player games do not fit into the established reinforcement-learning framework since the optimality criterion for games is not one of maximizing reward in the face of a fixed environment, but one of maximizing reward against an optimal adversary (minimax). Nonetheless, reinforcement-learning algorithms can be adapted to work for a very general class of games [63] and many researchers have used reinforcement learning in these environments. One application, spectacularly far ahead of its time, was Samuel's checkers playing system [99]. This learned a value function represented by a linear function approximator, and employed a training scheme similar to the updates used in value iteration, temporal differences and Q-learning.
More recently, Tesauro [118, 119, 120] applied the temporal difference algorithm to backgammon. Backgammon has approximately 1020 states, making table-based reinforcement learning impossible. Instead, Tesauro used a backpropagation-based three-layer neural network as a function approximator for the value function
![]()
Two versions of the learning algorithm were used. The first, which we will call Basic TD-Gammon, used very little predefined knowledge of the game, and the representation of a board position was virtually a raw encoding, sufficiently powerful only to permit the neural network to distinguish between conceptually different positions. The second, TD-Gammon, was provided with the same raw state information supplemented by a number of hand-crafted features of backgammon board positions. Providing hand-crafted features in this manner is a good example of how inductive biases from human knowledge of the task can be supplied to a learning algorithm.
The training of both learning algorithms required several months of computer time, and was achieved by constant self-play. No exploration strategy was used--the system always greedily chose the move with the largest expected probability of victory. This naive exploration strategy proved entirely adequate for this environment, which is perhaps surprising given the considerable work in the reinforcement-learning literature which has produced numerous counter-examples to show that greedy exploration can lead to poor learning performance. Backgammon, however, has two important properties. Firstly, whatever policy is followed, every game is guaranteed to end in finite time, meaning that useful reward information is obtained fairly frequently. Secondly, the state transitions are sufficiently stochastic that independent of the policy, all states will occasionally be visited--a wrong initial value function has little danger of starving us from visiting a critical part of state space from which important information could be obtained.
The results (Table 2) of TD-Gammon are impressive. It has competed at the very top level of international human play. Basic TD-Gammon played respectably, but not at a professional standard.
| Training Games | Hidden Units | Results | |
| Basic | Poor | ||
| TD 1.0 | 300,000 | 80 | Lost by 13 points in 51 games |
| TD 2.0 | 800,000 | 40 | Lost by 7 points in 38 games |
| TD 2.1 | 1,500,000 | 80 | Lost by 1 point in 40 games |
Although experiments with other games have in some cases produced interesting learning behavior, no success close to that of TD-Gammon has been repeated. Other games that have been studied include Go [104] and Chess [122]. It is still an open question as to if and how the success of TD-Gammon can be repeated in other domains.
In recent years there have been many robotics and control applications that have used reinforcement learning. Here we will concentrate on the following four examples, although many other interesting ongoing robotics investigations are underway.
The juggling robot learned a world model from experience, which was generalized to unvisited states by a function approximation scheme known as locally weighted regression [25, 82]. Between each trial, a form of dynamic programming specific to linear control policies and locally linear transitions was used to improve the policy. The form of dynamic programming is known as linear-quadratic-regulator design [97].

Figure 11: Schaal and Atkeson's devil-sticking robot. The
tapered stick is hit alternately by each of the two hand sticks. The task
is to keep the devil stick from falling for as many hits as possible. The
robot has three motors indicated by torque vectors ![]() .
.
Such tasks are controlled by machinery which operates according to various setpoints. Conventional practice is that setpoints are chosen by human operators, but this choice is not easy as it is dependent on the current product characteristics and the current task constraints. The dependency is often difficult to model and highly non-linear. The task was posed as a finite-horizon Markov decision task in which the state of the system is a function of the product characteristics, the amount of time remaining in the production shift and the mean wastage and percent below declared in the shift so far. The system was discretized into 200,000 discrete states and local weighted regression was used to learn and generalize a transition model. Prioritized sweeping was used to maintain an optimal value function as each new piece of transition information was obtained. In simulated experiments the savings were considerable, typically with wastage reduced by a factor of ten. Since then the system has been deployed successfully in several factories within the United States.
Some interesting aspects of practical reinforcement learning come to light from these examples. The most striking is that in all cases, to make a real system work it proved necessary to supplement the fundamental algorithm with extra pre-programmed knowledge. Supplying extra knowledge comes at a price: more human effort and insight is required and the system is subsequently less autonomous. But it is also clear that for tasks such as these, a knowledge-free approach would not have achieved worthwhile performance within the finite lifetime of the robots.
What forms did this pre-programmed knowledge take? It included an assumption of linearity for the juggling robot's policy, a manual breaking up of the task into subtasks for the two mobile-robot examples, while the box-pusher also used a clustering technique for the Q values which assumed locally consistent Q values. The four disk-collecting robots additionally used a manually discretized state space. The packaging example had far fewer dimensions and so required correspondingly weaker assumptions, but there, too, the assumption of local piecewise continuity in the transition model enabled massive reductions in the amount of learning data required.
The exploration strategies are interesting too. The juggler used careful statistical analysis to judge where to profitably experiment. However, both mobile robot applications were able to learn well with greedy exploration--always exploiting without deliberate exploration. The packaging task used optimism in the face of uncertainty. None of these strategies mirrors theoretically optimal (but computationally intractable) exploration, and yet all proved adequate.
Finally, it is also worth considering the computational regimes of these experiments. They were all very different, which indicates that the differing computational demands of various reinforcement learning algorithms do indeed have an array of differing applications. The juggler needed to make very fast decisions with low latency between each hit, but had long periods (30 seconds and more) between each trial to consolidate the experiences collected on the previous trial and to perform the more aggressive computation necessary to produce a new reactive controller on the next trial. The box-pushing robot was meant to operate autonomously for hours and so had to make decisions with a uniform length control cycle. The cycle was sufficiently long for quite substantial computations beyond simple Q-learning backups. The four disk-collecting robots were particularly interesting. Each robot had a short life of less than 20 minutes (due to battery constraints) meaning that substantial number crunching was impractical, and any significant combinatorial search would have used a significant fraction of the robot's learning lifetime. The packaging task had easy constraints. One decision was needed every few minutes. This provided opportunities for fully computing the optimal value function for the 200,000-state system between every control cycle, in addition to performing massive cross-validation-based optimization of the transition model being learned.
A great deal of further work is currently in progress on practical implementations of reinforcement learning. The insights and task constraints that they produce will have an important effect on shaping the kind of algorithms that are developed in future.
There are a variety of reinforcement-learning techniques that work effectively on a variety of small problems. But very few of these techniques scale well to larger problems. This is not because researchers have done a bad job of inventing learning techniques, but because it is very difficult to solve arbitrary problems in the general case. In order to solve highly complex problems, we must give up tabula rasa learning techniques and begin to incorporate bias that will give leverage to the learning process.
The necessary bias can come in a variety of forms, including the following:
With appropriate biases, supplied by human programmers or teachers, complex reinforcement-learning problems will eventually be solvable. There is still much work to be done and many interesting questions remaining for learning techniques and especially regarding methods for approximating, decomposing, and incorporating bias into problems.