ФОРМИРОВАНИЕ ОПТИМАЛЬНОГО ИНВЕСТИЦИОННОГО ПОРТФЕЛЯ С ПОМОЩЬЮ СРЕДЫ ОБРАБОТКИ ДАННЫХ MATLAB 6.0

Евтюшкина Т.Б., ДонНТУ, каф. ПМиИ

evtanya@ukrtop.com

Руководитель: Григорьев А.В. к. т. н. доц. каф. ПМиИ

Abstract

Yevtyushkina T. B. Formation of the optimum investment portfolio by means of surrounding data processing MatLab 6.0

In conditions of the developed market economy the important component is necessity of definition sufficiency a degree of investment appeal to investments into the certain enterprise. That is estimations of the boundary price of shares. To create effective investment portfolio, the basic attention should be concentrated on search of ways  optimization of structure a portfolio of securities and a choice of strategy its formation that demands research of all complex investment process.

In conditions of a developing share market of Ukraine and imperfection of the legislation it is very difficult for majority of investors to choose shares of this or that company for investment of the capital. The given article will help investors to throw light on the dark sides of process of formation an investment portfolio.

At formation of a portfolio of investments the problem appears to each investor, how it is more favorable to invest the capital to receive the maximal profitableness at the minimal risk what shares of the companies are the most attractive to investment. These very important problems are researched in the given article.

In article the way of formation of an optimum investment portfolio by means of a package of applied programs for financial calculations of system MatLab is presented. And also the analysis of the statistical given shares of the companies which enter into index PFTS has been lead. Therefore the optimum investment portfolio has been generated.

Введение

В условиях развитой рыночной экономики важной составляющей является необходимость определения достаточности степени инвестиционной привлекательности для осуществления инвестиций в определенное предприятие, то есть оценки граничной цены акций, при которой инвестиция в данное предприятие является оправданной. Руководствуясь целью создания эффективного инвестиционного портфеля, основное внимание следует сосредоточить на поиске путей оптимизации структуры портфеля ценных бумаг и выборе стратегии его формирования, что требует исследования всего комплекса инвестиционного процесса.

При осуществлении портфельного инвестирования перед субъектами инвестирования предстают проблемы эффективного вложения финансовых ресурсов. Важной проблемой при этом является выделение отдельных этапов процедуры сравнения экономической эффективности портфельного инвестирования и определения комплекса мер, которые непосредственно влияют на безопасность инвестиционных вложений.

Портфель ценных бумаг требует частого корректирования в связи с высокой динамикой рынка ценных бумаг, а в условиях Украины необходимость такого корректирования в значительной мере усиливается нестабильностью и неравномерностью развития фондового рынка. Именно поэтому проведение процедуры сравнения эффективности портфеля ценных бумаг требует объективной оценки процессов, которые происходят на фондовом рынке, выявление и анализ основных тенденций, которые определяют развитие инвестиционного процесса и влияют на взаимосвязи между участниками фондового рынка.

1 Управление формированием инвестиционного портфеля

Формирование портфеля ценных бумаг, являясь составной частью инвестиционного процесса, включает в себя определение конкретных активов для вложения средств, а также пропорций (весов) распределения инвестируемого капитала между активами. Главная задача менеджеров по управлению портфелями инвестиций с точки зрения современной теории формирования портфеля заключается в достижении наилучшего возможного компромисса между возможными риском и доходностью. Основные положения этого подхода, сформулированные Г. Марковицем в 1952г., заключаются в следующем:

• предполагается, что в настоящий момент времени, обозначенный как t = 0, инвестор имеет некоторую сумму денег для инвестирования;
• деньги инвестируются в конкретные ценные бумаги, которые будут находиться в портфеле инвестора в течение определенного промежутка времени, называемого периодом владения, до момента времени, обозначенного как t = 1;
• в конце периода владения инвестор продает ценные бумаги, которые были куплены в начале периода владения при t = 0;
• доходности ценных бумаг и всего портфеля рассматриваются как случай­ные величины, так как в момент принятия решения инвестор не может абсолютно точно спрогнозировать доходность ценных бумаг и портфеля на предстоящий период владения;
• доходности ценных бумаг и всего портфеля, определяемые как случай­ные величины, характеризуются ожидаемыми (или средними) значе­ниями и стандартными отклонениями. Ожидаемая доходность может быть представлена как мера потенциального вознаграждения, связанная с конкретным портфелем, а стандартное отклонение - как мера риска, связанная с данным портфелем;
• задача инвестора состоит в нахождении в момент времени t = 0 при покуп­ке ценных бумаг сбалансированного решения на основе оценок ожидаемой доходности и ожидаемого риска каждого из возможных портфелей.

Ожидаемая доходность портфеля ценных бумаг R_p определяется как средневзвешенная доходность ценных бумаг, составляющих компоненты портфеля

где N - число ценных бумаг в портфеле;

W_i – вес i-й ценной бумаги в портфеле;

r_i – ожидаемая доходность i-й ценной бумаги.

Из уравнения следует, что инвестор, который желает получить наибольшую ожидаемую доходность, должен просто приобрести портфель, состоящий из одной ценной бумаги с наибольшей доходностью. Однако, как правило, инвесторы стремятся получить высокую доходность при усло­вии, чтобы "доходность была настолько определенной, насколько это воз­можно". Вследствие этого инвесторы должны диверсифицировать порт­фель, т. е. включать в него более одной ценной бумаги, так как диверси­фикация может снизить риск, измеряемый стандартным отклонением.

Дисперсия портфеля, состоящего из N ценных бумаг, вычисляется по формуле:

где cov_ij - ковариация активов i и j.

Если предположить, что одинаковые суммы инвестированы в каждый из N активов, дисперсию портфеля можно представить в следующем виде:

Первое слагаемое в этом выражении является средней дисперсией цен­ных бумаг портфеля, умноженной на 1/N. При увеличении числа активов в портфеле множитель 1/N уменьшается, и соответственно первое слагаемое при росте N уменьшается, приближаясь к нулю. Второе слагаемое представ­ляет собой среднюю ковариацию, умноженную на множитель (N-1)/N, ко­торый при увеличении N стремится к единице. Исходя из этого можно сде­лать вывод, что дисперсия портфеля, диверсифицированного включением большого количества активов с равными весами для всех активов, прибли­жается к средней ковариации отдельных активов. В случае, если ожидаемые доходности всех активов независимы, т. е. все cov_ij = 0, дисперсия портфеля стремится к нулю при росте N.

Для портфелей, составляемых из фиксированного набора активов, от­ношение риск/доходность изменяется с изменением структуры портфеля, определяемого множеством {W_i}. Инвестор выбирает свой портфель таким образом, чтобы обеспечить максимальную ожидаемую доходность для некоторого уровня риска или обеспечить минимальный риск для некоторого значения ожидаемой доходности.

Эта задача может быть записана в следующем виде:

 min   (W'WW)

{W_i}

при  ,  ,

где W - вектор, компонентами которого служат веса активов портфеля W_i*,

W - ковариационная матрица доходностей активов;

R_o - минимальный приемлемый уровень доходности портфеля.

Портфели, которые максимизируют доходность при заданном риске, или, наоборот, минимизируют риск при заданной доходности, называются эффек­тивными. Эффективные портфели на плоскости риск/доходность определяют; линию, называемую эффективной границей или эффективным фронтом. Эффективная граница Марковица представляет собой вогнутую кривую и имеет положительный наклон, т. е. отрезок, соединяющий любые две точки грани­цы, лежит ниже этой границы. Для определения структуры любого из эффек­тивных портфелей Марковицем был предложен метод решения, который включает в себя алгоритм квадратичного программирования, известный как метод критических линий.

После того как определена эффективная граница, инвестор выбирает оптимальный портфель. Выбор наиболее желательного портфеля связан с отношением инвестора к риску или, точнее, со степенью его неприятия рис­ка. Уровень неприятия риска может быть охарактеризован с помощью кри­вой безразличия инвестора к риску. Эта кривая состоит из семейства пар отношений риск/доходность, соответствующих компромиссу между ожидаемой доходностью и риском, и может быть представлена как двумер­ный график, где по горизонтальной оси откладывается риск, мерой которого является стандартное отклонение, а по вертикальной оси - вознаграждение, мерой которого является ожидаемая доходность. Кривая безразличия уста­навливает приращение доходности, которое конкретный инвестор будет требовать, чтобы сделать риск имеющим смысл.

2 Возможности среды обработки данных MatLab 6.0

 Система MatLab и пакет прикладных программ для финансовых расчетов Financial Toolbox обеспечивают в полной мере интегрированную вычислительную среду для проведения инженерных и аналитических финансовых расчетов. Пакет включает 151 специализированную функцию, что позволяет решать задачи практически любой сложности, возникающие в процессе математического и статистического анализа финансовых данных, обеспечивая их необходимой интерпретацией и высококачественной графикой.

Пакет прикладных программ Financial Toolbox (ППП FT) поставляется с большим числом программных текстов, демонстрирующих возможности и особенности этого функционального пакета, включая построение графиков и диаграмм, портфельный анализ, ценообразование опционов и т.д.

Классификация инструментальных средств ППП FT:

• вычисление и преобразование дат;
• форматирование денежных сумм и построение финансовых диаграмм;
• вычисление и анализ денежных потоков;
  • определение стоимости и доходности ценных бумаг с фиксированными поступлениями; анализ временной структуры процентных ставок;
  • оценка и анализ деривативов ценных бумаг;
  • портфельный анализ.

В ППП FT включены функции, предназначенные для решения пробле­мы нахождения портфеля, удовлетворяющего наилучшим образом требова­ниям инвестора при учете всех необходимых параметров и ограничений. Эти функции в зависимости от решаемых ими задач могут быть разделены на три категории:

1. Функции оптимизации портфеля.
2. Функции   формирования  ограничений  для  весовых   коэффициентов портфеля.
3. Функции вычисления стоимости и доходности портфеля и входящих в него активов.

3 Построение эффективной границы Марковица в ППП FT

В ППП FT задача построения эффективной границы Марковица решается с помощью функции квадратичного программирования qp пакета Optim.

Для представления кривой неприятия риска в ППП FT используется следующее уравнение:

U = E(r)-0.5As²,

где U - ожидаемая полезность кривой безразличия, определяющая точку пересечения с вертикальной осью;

Е (r) - ожидаемая доходность;

А - индекс неприятия риска инвестором;

s - среднеквадратичное отклонение.

Типичные значения коэффициентов неприятия риска колеблются между 2.0 и 4.0 с большим значением для лиц, имеющих меньшую толерантность к риску. На рис. 1 показаны кривые безразличия для двух индексов неприятия риска.

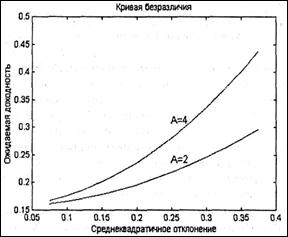
Рисунок 1 – Кривые безразличия

Кривые безразличия имеют два важных свойства: 1) все портфели, ле­жащие на одной кривой безразличия, равноценны для инвестора; 2) инве­стор считает любой портфель, лежащий на кривой безразличия, которая находится выше и левее, привлекательнее любого портфеля, лежащего на кривой безразличия, которая находится ниже и правее. Отсюда следует, что оптимальный портфель О* соответствует точке, в которой кривая без­различия касается эффективной границы (рис. 2).

Рисунок 2 – оптимальный портфель

Проблема выбора адекватного портфеля инвестором при возможности безрискового кредитования и безрискового заимствования представляет: обобщение подхода Марковица к инвестированию. Определение линии размещения капитала (прямой линии, касательной к эффективному фронту и исходящей из точки безрисковой ставки кредитования/заимствования) и нахождение на ней точки, соответствующей оптимальному портфелю, в  общем случае зависит от профиля отношения риск/доходность, безрисковой процентной ставки кредитования, безрисковой процентной ставки заимст­вования и степени неприятия риска инвестора.

Для нахождения оптимального портфеля при возможности безрисковых кредитования и заимствования необходимо определить эффективную гра­ницу, которая отличается от эффективной границы Марковица. Для этой цели необходимо определить портфель Т, который соответствует точке ка­сания линии размещения капитала с эффективным фронтом Марковица (рис. 3). Ожидаемая доходность любого портфеля r_р на этой прямой мо­жет быть представлена в следующем виде:

r_р=mr_f+(1 -m)r_T,

где r_f- безрисковая ставка кредитования (заимствования);

m  - вес безрискового кредитования (заимствования).

Оптимальным портфелем О* для инвестора будет портфель, который соответствует точке касания кривой безразличия инвестора с эффективной границей. При этом m определяется как

где s₀* — дисперсия общего оптимального портфеля;

s_T - дисперсия портфеля Т.

При допустимости инвестирования в безрисковый актив (безрисковое кредитование) эффективная граница приобретает вид прямого отрезка, ис­ходящего из точки, соответствующей безрисковой процентной ставке кре­дитования, к точке касания с эффективной границей Марковица Т, а также части эффективного множества Марковица, лежащей выше и правее точки касания. В этом случае, в зависимости от степени избегания риска инвесто­ром, оптимальный портфель будет состоять либо из вложений части на­чального капитала в безрисковый актив и остальной части капитала в порт­фель Т, либо только из рискованного портфеля Т, если инвестор менее склонен избегать риска (рис. 3).

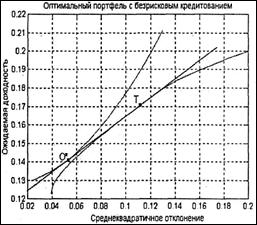
Рисунок 3 – Оптимальный портфель с безрисковым кредитованием

В случае, если рискованный портфель покупается на собственные и за­емные средства, эффективная граница будет представлять собой продолже­ние луча, который выходит из точки, соответствующей безрисковой ставке заимствования, и проходит через точку, соответствующую касательному портфелю Т, и участок эффективной границы, лежащий ниже и левее каса­тельного портфеля Т (рис. 4). Оптимальный портфель в зависимости от степени неприятия риска инвестором будет составлен из получения займа инвестором по безрисковой ставке и инвестиции этих и собственных фон­дов в портфель Т или только из рискованного портфеля Т.

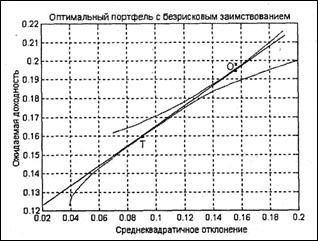
Рисунок 4 – Оптимальный портфель с безрисковым заимствованием

При возможности безрискового кредитования и безрискового заимство­вания и разных ставках предоставления и получения займа эффективное множество состоит из трех различных соединенных между собой частей (рис. 5). Первой частью является отрезок касательной прямой к эффективной границе, проведенный через точку, определяемую безрисковой ставкой кредитования, который представляет собой комбинации различных «объемов безрискового кредитования в сочетании с инвестированием в портфель рискованных активов Т1. Вторая часть является участком эффектив­ной границы Марковица между точками Т1 и Т2, представляющим собой «инвестиции в рискованный портфель. Третьей частью является луч, исхо­дящий из точки, определяемой безрисковой ставкой заимствования, каса­тельно к эффективной границе начиная от точки касания Т2. Эта часть эффективной границы представляет различные комбинации безрискового  заимствования в сочетании с инвестированием в рискованный портфель.

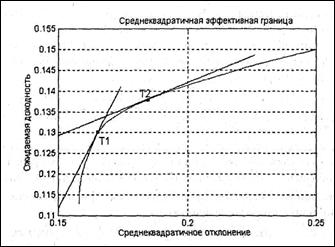
Рисунок 5 – Эффективное множество

Оптимальным портфелем для инвестора будет портфель, который соответ­ствует точке касания кривой безразличия инвестора с эффективной границей. В зависимости от вида кривых безразличия точка касания может оказаться на любом из трех сегментов, составляющих эффективную границу.

На портфель могут быть наложены дополнительные требования, кото­рые определяют отношения, связанные с заранее заданными ограничениями на осуществление инвестиций в различные активы или группы активов. Эти ограничения могут быть представлены как в форме равенств (например, сумма весов должна быть равна 1), так и в форме неравенств (например, при запрете на короткую продажу все активы должны иметь вес в портфеле, больший 0).

3 Оптимизация инвестиционного портфеля на основе статистических данных ПФТС

Для формирования оптимального инвестиционного портфеля возьмем акции компаний, которые входят в индекс Первой фондовой торговой системы (ПФТС). В 2004г. в индекс ПФТС были включены акции следующих компаний (табл. 1).

Таблица 1 – Компании, акции которых представлены в индексе ПФТС

Исходными данными для анализа послужили данные о ценах на акции 2004г. Инвестиционный горизонт – 1 год. Статистическая база данных по акциям компаний представляет собой совокупность неоднородных рядов. Для анализа необходимо усреднить их – взять за каждый месяц среднюю цену. Результатом этого стала таблица 2.

Таблица 2 – Среднемесячные цены акций за 2004г., грн.

Далее рассчитаем среднемесячные доходности акций по формуле:

где Т – срок инвестиционного горизонта;

I_T – цена акции в конце периода;

I₀ – цена акции в начале периода.

Таблица 3 – Среднемесячные доходности акций

Ковариация доходностей рассчитывается по следующей формуле:

.

Для определения ожидаемой доходности акций и ковариационной матрицы по рядам доходности воспользуемся функцией [ExpRetern, ExpCovariance, NumEffObs] = ewstats(RetSeries, DecayFactor, WindowLength)

RetSeries =

[ExpReturn, ExpCovariance, NumEffObs]= ewstats(RetSeries)

ExpReturn =

ExpCovariance =

NumEffObs = 10

Количество портфелей, формируемых вдоль эффективной границы

NumPorts=14;

[PortRisk, PortReturn, PortWts]=frontcon(ExpReturn,ExpCovariance,NumPorts)

PortRisk =

PortReturn =

PortWts =

Применение функции frontcon(ExpReturn,ExpCovariance,NumPorts)без выходных параметров приводит к построению графика эффективной границы, который приведен на рисунке 6.

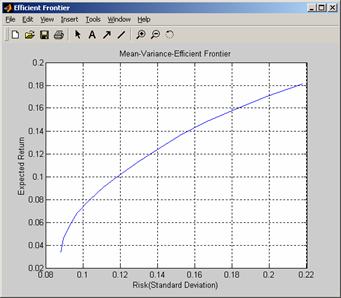
Рисунок 6 – График Эффективной границы

Теперь найдем оптимальный рисковый портфель и оптимальное размещение фондов между портфелем с риском и и безрисковым активом, используя следующие значения

RisklessRate=0.08; безрисковая ставка

BorrowRate=0.12; ставка заимствования

RiskAversion=3; неприятие риска инвестором

Вызов функции Portalloc с указанием выходных параметров возвращает дисперсию (RiskyRisk), ожидаемую доходность (RiskyReturn) и веса (RiskyWts) активов, размещаемых в оптимальном рисковом портфеле. При этом вычисляется также доля (RiskyFraction) полного портфеля, распределенного в рисковый портфель, дисперсия (OverallRisk) и ожидаемая доходность общего портфеля (OverallReturn). В общем портфеле скомбинированы инвестиции в безрисковые активы и в рисковый портфель. Реальное распределение, предназначаемое каждому из этих вложений, определяется степенью неприятия риска, характеризующей инвестора.

[RiskyRisk, RiskyReturn, RiskyWts, RiskyFraction, OverallRisk, OverallReturn] = Portalloc(PortRisk,PortReturn,PortWts,RisklessRate,BorrowRate,RiskAversion)

RiskyRisk = 0.2178

RiskyReturn = 0.1814

RiskyWts =

RiskyFraction = 0.7127

OverallRisk = 0.1552

OverallReturn = 0.1523

Применение функции Portalloc(PortRisk, PortReturn, PortWts, RisklessRate, BorrowRate, RiskAversion) без выходных параметров приводит к построению графика эффективной границы, на котором отображены критические точки (рис. 7). ans = 0.2178

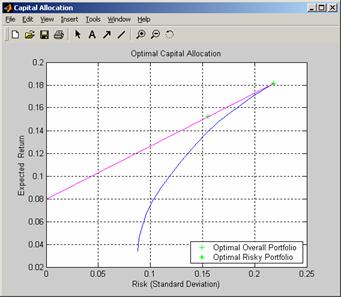
Рисунок 7 – Оптимальное размещение капитала

При изменении безрисковой ставки RisklessRate=0.06; меняется и график оптимального размещения капитала (рис 8). ans = 0.2178

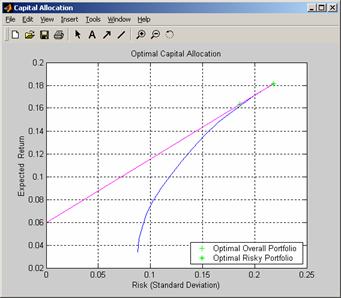
Рисунок 8 - График оптимального размещения капитала

[RiskyRisk, RiskyReturn, RiskyWts, RiskyFraction, OverallRisk, OverallReturn] = Portalloc(PortRisk,PortReturn,PortWts,RisklessRate,BorrowRate,RiskAversion)

RiskyRisk = 0.2178

RiskyReturn = 0.1814

RiskyWts =

RiskyFraction = 0.8533

OverallRisk = 0.1858

OverallReturn = 0.1636

При сравнении полученных результатов с различными безрисковыми ставками доходностей, можно сказать, что дисперсия, ожидаемая доходность и веса активов не изменились, а доля полного портфеля, распределенного в рисковый портфель, дисперсия и ожидаемая доходность общего портфеля увеличились.

Выбор оптимального портфеля из множества эффективных портфелей зависит от того, как выглядит функция ценностей инвестора, которая формирует его личное восприятия соотношения «риск-доходность». На рисунке 9 представлена структура портфеля с минимальным риском.

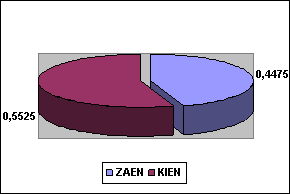
Рисунок 9 – Портфель с минимальным риском

Несмотря на то, что в принципе инвесторы при составлении портфеля могут выбрать среди тысячи разнообразных активов, на практике их выбор ограничивается несколькими продуктами, которые предлагают им финансовые посредники. К ним относятся банковские счета, взаимные фонды, состоящие из акций и облигаций, а также недвижимость. При разработке и составлении списка активов, предлагаемых клиентам, компании-посредники используют новейшие достижения финансовых технологий.

Заключение

В работе представлен способ формирования оптимального инвестиционного портфеля с помощью пакета прикладных программ для финансовых расчетов системы MatLab.

В работе был проведен анализ статистических данных акций компаний, которые входят в индекс ПФТС. В результате чего был сформирован оптимальный инвестиционный портфель.

В условия развивающегося фондового рынка Украины и несовершенства законодательства большинству инвесторов очень сложно выбрать акции той или иной компании для инвестирования капитала. Данная работа поможет инвесторам пролить свет на темные стороны процесса формирования инвестиционного портфеля.

Литература

1. А.Ф. Гукалюк, Процедура порівняння ефективності портфеля цінних паперів як елемент визначення інвестиційної привабливості. //Актуальні проблеми економіки №4(22), 2003.
2. Богдан Луців, Портфельне інвестування в діяльності комерційних банків. // Банківська справа, №5, 2000р.
3. Шапкин А.С. Экономические и финансовые риски: Оценка управления, портфель инвестиций. – Киев, 2003г.
4. Боли, Зви, Кейн, Алекс, Маркус, Алан. Принципы инвестиций, четвертое издание: Пер. с англ. – М.: Издательский дом «Вильямс», 2002. – 948с.
5. И. Поддубный, Анализ инвестиционной привлекательности в расчеты «разумной» цены акции ОАО, которые предлагаются на 74 СА за денежные средства с 2 по 11 ноября 2004г. // Фондовый рынок №39, 2004г.
6. А. Камінський, О. Шепелява, Портфельне інвестування в Україні: статистичний підхід. // Банківська справа, №6, 2000р.
7. К.Н., Цыплакова Т.П. Финансовая аналитика. MATLAB 6/ Под общ. ред. к. т. н. В. Г. Потемкина. – М.: ДИАЛОГ-МИФИ, 2001. – 386с. – (Пакеты прикладных программ; Кн. 3).
8. Финансовая компания «Кинто». Недельные обзоры финансового рынка. http://www.kinto.com/rus/research/weekly.html