|
Автор: Paul Harbunou
Начало
Автор о своей статье.
Вашему вниманию предоставляется описание очень простого
в реализации способа работы с ландшафтами. Возможно,
его основная особенность — это минимальное использование
вычислений на FPU. На сегодняшний день, кажется, у
каждого есть видеокарта с названием GeForce или Radeon,
и мы можем себе немножко позволить разгрузить CPU за
счет нагрузки на GPU. В разумных пределах конечно,
хотя пределы очень зависят от разума. Начнете спорить
— начну соглашаться.
Статья в основном рассказывает об альтернативном способе
работы с ландшафтами, который разработан из расчета
на использование в моем личном проекте (только слегка
переделанный).
Сразу отмечу, что речь не идет о чем-то революционном
и новом.
Речь идет об оптимизации, и о том, как можно отказаться
от вычислительно емких (кстати, это очень спорно) методов,
таких как Quadtree или Octree. Я не в коем случае не
буду спорить, что QuadTree лучше моего метода или тем
более спорить о преимуществах использования Octree.
С последним сравнивать мой метод просто нельзя.
Как вы догадались – основной задачей статьи ставится
старая проблема: как изображать только ту часть ландшафта
(сцены), которая видна в камере.
Я в первую очередь задумывался о том, что, может быть,
не стоит тратить время CPU, выясняя то, какой же там
кусочек сцены попадает в поле видимости, а какой —
нет. Ведь, сегодня у каждого есть очень неплохая видеокарта
и иногда, быстрей изобразить то, что не видно, чем
выяснять видим ли мы это или не видим, загружая CPU.
Также, я собираюсь немного обсудить проблему размера
проекта. Связано это с тем, что, начиная проект без
приличного финансового запаса, можно его запросто загубить.
Именно управление объемом продукта позволит хотя бы
закончить проект как shareware. Кроме того, управление
объемом может значительно уменьшить размер демо-версии,
готовящегося продукта.
Карты
Итак, приступим.
Сразу опишем используемые карты:
HMAP (height map): карта высот. Для примера,
возьмем размер 4096x4096.
TMAP (texture id map): карта
идентификаторов текстур. Для примера, возьмем
размер 512x512.
SMAP (shadow map): карта теней. Для
примера, возьмем размер 4096x4096, т.е. равный
карте высот.
OMAP (object map): карта идентификаторов
объектов. Для примера, возьмем размер 4096x4096.
Подробней о HMAP
Пусть вся карта высот (HMAP) имеет размер 4096x4096.
Надеюсь, этот размер сегодня никого не пугает. Всего:
4096*4096*2= 33.554.432 треугольников.
Мы можем хранить карту высот даже в JPG формате. Желательно,
хранить не Grayscale, а только один компонент (к примеру,
синий). Это может значительно уменьшить размер JPG
файла.
И не обязательно использовать для этого размер 4096x4096.
Можно хранить с размером 2048x2048 (а то и с 1024x1024),
а когда загружаем из JPG, используя bicubic scaling,
увеличивать размер до 4096x4096. Если качество JPG
было не очень хорошее (меньше 50-60%), то bicubic scaling
слегка сгладит артефакты от компрессии. Если этого
недостаточно, то применим blur, точней нечто похожее
на него:
// array – указатель на 8битное изображение
// image_width, image_height – размеры изображения
// depth – глубина для blur изображения
BOOL SomethingLikeBlur(unsigned char *array, long image_width, long image_height, long depth)
{
long a,d,n,m00,m10, i32;
m00=0;
for (d=0; d< depth; d++) {
for (a=0;a<image_height-1;a++) {
for (n=0;image_width-1;n++) {
// m01= m00+1;
// m11= m00+ image_width+1;
m10= m00+ image_width;
i32=((long)array[m00]+ (long)array[m00+1]+ (long)array[m10+1]+ (long)array[m10])>>2;
if (i32>0xFF) {
array[m00]= (unsigned char)0xFF;
} else {
array[m00]=(unsigned char)i32;
}
m00+=1;
}
}
}
return (TRUE);
|
Но полностью избавиться от артефактов не удастся в
любом случае, поэтому лучше хранить в JPEG с качеством
70-80%.
Да, наверное, вы уже догадались, что метод, который
здесь будет изложен подходит и для shareware игр. На
это указывает использование JPG (причем низкого качества)
и увеличение размера карты высот на этапе загрузки.
Подробней о TMAP
Введем понятие карты текстурных идентификаторов (TMAP).
TMAP — это карта, где хранятся идентификаторы текстур
(это могут быть 8 битные или 16 битные идентификаторы.
В зависимости от того, сколько может использоваться
текстур для изображения ландшафта в вашем проекте).
Пусть размер этой карты будет 512x512 и накладываться
эта карта будет на HMAP (карта высот). Так как размеры
HMAP относятся к TMAP как 4096/512 (=8), то на
каждую точку TMAP приходится площадь 8x8 карты высот
(HMAP).
Подробней об OMAP
Теперь у нас есть ландшафт, с нанесенными на него
текстурами. Пора добавить на сцену объекты, т.е. камни,
деревья, траву, дома.
И для этого у нас есть карта идентификаторов (OMAP)
размером 4096x4096, но хранить на диске её как карту
нет необходимости. На диске можно хранить таблицу объектов.
Разумеется с описанием назначений объектов и координатами
на карте OMAP.
Подробней о SMAP
Тени пока обсуждать не будем, т.к. делать их можно
очень по-разному.
Ограничимся примитивным способом. Берем готовую сцену
в нашем редакторе уровней. Камеру направляем перпендикулярно
поверхности и делаем скриншот всей сцены c высоты птичьего
полета. Желательно, скриншот делать без поверхности,
т.е. только объектам. Далее скриншот попадает в Photoshop.
Сначала, изображение подвергается нехитрым операциям
Color Balance (не тот Color balance, что в Photoshop-е
обозначен, а в смысле управления Hue, Saturation, Brightness,
Contrast, Gamma). Делаем Motion Blur под нужным углом,
переводим все в Grayscale (или Desaturate) и вот у
нас есть карта теней. Если Motion blur был глубокий,
то значит на сцене закат или восход, если motion blur
легкий, то полдень.
Подготовка
Ну а теперь мы подошли к главному вопросу. Нам нужно
отрендерить видимую часть сцены, исходя из информации
о положении камеры на ней. Для внедрения обсуждаемого
метода рендеринга сцены нам потребуется знать позицию
камеры на карте TMAP, угол поворота камеры (точнее,
все, что нужно из YPR – это только yaw) и FOV камеры.
Чтобы изображать то, что действительно будет «видеть»
камера, мы должны нанести на карту TMAP маску (Рисунок
1). Пусть маска имеет размер 32x32.
На рисунке 1 маска сделана для случая, когда FOV 90
градусов. Разумеется, что могут быть и другие случаи.
Если в игре требуется изменить FOV, то придется сделать
несколько масок и подставлять нужную маску для вашего
случая.
Это можно отнести к минусам метода. Как вы можете
догадываться, то полет над ландшафтом тоже исключен.
Камера не должна слишком высоко отрываться от поверхности.
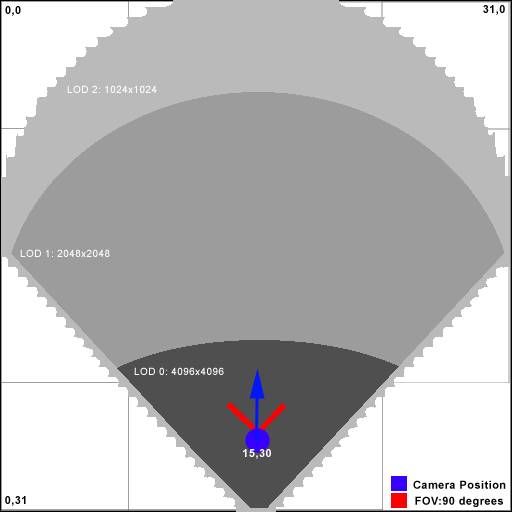
Рисунок 1. Маска 32x32.
Как нужно работать с маской? Маску нужно поворачивать
вокруг выбранной точки, которая является местом
положения камеры. Проще некуда, для этого нам требуется
написать функцию вращения маски.
Сразу отмечу, что функция вращения будет оптимизирована
для вычислений в целых величинах, т.к. в применении
вещественных (float) смысла большого нет.
Сначала нужно задать кол-во углов в круге:
#define BR_ANGLES 8192
Величина 8192 выбрана не случайно. Будем считать,
что разрешение экрана 2048x1536 будет максимально допустимым
в игре. Пусть мы имеем FOV 90 градусам. Это значит,
что 360/90 = 4, т.е. грубо говоря, в 360 градусной
панораме у нас будет 4 “экрана” по 2048 горизонтальных
пикселей, а 2048 * 4 = 8192. Это и есть наша величина.
Изменение на единицу нашего угла будет означать, что
при разрешении 2048x1536 сцена “повернется” по горизонтали
на один пиксель. На разрешении 1024x768 даст такой
же результат изменение угла на 2 значения.
Теперь определим размеры TMAP:
#define BR_MAP_W 512 // width
#define BR_MAP_H 512 // height
#define BR_MAP_SIZE (BR_MAP_W*BR_MAP_H)
сдвиг влево или вправо 9 означает умножение или деление
на 512:
#define BR_MAP_S 9 // shift
здесь мы вычисляем координаты x,y на одномерном массиве
карты:
#define BR_MAP(x,y) (((x)&(BR_MAP_W-1)) + (((y)&(BR_MAP_W-1))<<BR_MAP_S))
Эта функция обнаруживает так же и выходы за пределы
карты.
К примеру, в выражении (x)&(BR_MAP_W-1) – если
x=513, то результат будет равен 1. Это то же самое,
что деление по модулю, только оптимизированное операцией
“&”.
Какими бы не были значения x и y – их координаты будут
переведены в область карты, что позволяет нам сделать
карту зацикленной.
В связи с этим, хотелось бы напомнить, что
Земля имеет геосферическую форму, но мы этим
можем пренебречь, развернув её в плоскость.
Но можно считать, что Земля - это плоскость,
лежащая на могучих спинах несчастных 3-ёх
китов, что успешно реализовано почти в каждой
сегодняшней игре.
Если мы не хотим, что бы карта была зацикленной, то
код меняется, но проверку для каждой точки на границы
карты делать не потребуется. В конце статьи поймете
почему. Зато строку #define BR_MAP(x,y) можно заменить
на:
#define BR_MAP(x,y) (x+ (y<<BR_MAP_S))
Теперь, по аналогии объявляем макросы для маски:
#define BR_MASK_W 32
#define BR_MASK_H 32
#define BR_MASK_S 5
#define BR_MASK_SIZE (BR_MASK_W*BR_MASK_H)
#define BR_MASK(x,y) (((x)&(BR_MASK_W-1)) + (((y)&(BR_MASK_W-1))<<BR_MASK_S))
Так как нет необходимости в использовании операций
с плавающей точкой, то нужно объявить 2 величины:
// задаем точность вычислений. (equal to (2<<(16-1)))
#define BR_MULT 65536
// это для сдвигов влево, вправо. 2 в 16ой степени и есть 65536.
#define BR_S 16
Где это применяется? Прежде чем описывать применение
– опишем структуру для простоты понимания, где будет
всё требующееся для вращения маской.
Определим типы (для удобства):
typedef unsigned char U8, *PU8; // 8-bit unsigned.
typedef signed long S32, *PS32; // 32-bit signed.
typedef struct _ODPoint
{
S32 x,y;
} ODPoint;
|
И сама структура:
typedef struct _BR {
U8 *map; // указатель на карту текстурных идентификаторов 512x512
U8 *mask; // указатель на маску 32x32
S32 sin[BR_ANGLES]; // таблица синусов
S32 cos[BR_ANGLES]; // таблица косинусов
S32 angle; // угол [0; 8191]
ODPoint masksize; // размер маски
ODPoint pos; // позиция камеры на карте map
ODPoint centre; // координата на маске, относительно которой будет производиться вращение
} BR;
|
Теперь вернемся к BR_MULT и BR_S.
Применяется это, прежде всего для составления таблицы
синусов и косинусов:
for (int n=0;n<BR_ANGLES;n++) {
BR.sin[n]=(S32)(sin((float)angle)*BR_MULT);
BR.cos[n]=(S32)(cos((float)angle)*BR_MULT);
angle=(float)n*M_2_PI/(float)(BR_ANGLES);
}
|
M_2_PI это (PI*2) и равно оно примерно 6.283185307179586232
Теперь у нас есть таблица синусов и косинусов, где
все значения умножены на 65536 и представлены как signed
long.
Страницы: 1 2
|