Введение

Если Вы пишите игру с открытым пространством Вам необходима оптимизация рендеринга ландшафта. Для рендеринга ландшафта со сложным рельефом нужны специальные алгоритмы оптимизации, так как сложнорельефный ландшафт содержит много полигонов, которые не в состоянии прорендерить современные компьютеры.

Этот учебник не очень структурирован и понятен, не все здесь будет разложено по полочкам - много в чем придется разбираться самому.
 

Представление ландшафта в форме height grid (height field)

Довольно распостраненный и популярный метод. Ландшафт представляет собой черно-белую карту высот - обычный графический файл размера SizeH*SizeW, где SizeH всегда равно SizeW. Файл считывается в массив, в котором дальше хранится. Высота рассчитывается просто - чем белее точка, тем выше вершина будет на ландшафте, чем чернее - тем ниже вершина.

Так-же мы можем генерировать ландшафт совершенно случайным образом, используя функцию синуса и косинуса:

#define AREA_SIZE       128             /* размер ландшафта */

// Function     : init_height_field
// Purpose      : Инициализация ландшафта с использованием функций синуса и косинуса
//
void init_height_field( void )
{
    float x, y;
    float h;
    for(x = 0; x < AREA_SIZE; x++)
    {
        for(y = 0; y < AREA_SIZE; y++)
        {
            h = 10.0 * sin(x/24.0) + 7.0 * cos((y-50.0)/18.0);
            height_field[(int)x][(int)y] = h;
        }
    }
}

Например, вот сгенерированная карта высот размером 129x129.

Рендерить ландшафт из карты высот очень просто и легко. В движках Протон2 и Протон3 мы использовали ландшафт в 3d формате - типа как файл 3D модели, нарисованной в 3DMAX. В результате чего ландшафт занимал огромный объем памяти, ландшафт тормозил при загрузке и рендеринге, нельзя было применить традиционные LOD алгоритмы оптимизации. Вывод - ландшафт как 3D модель можно использовать только когда он небольшой. В этой статье мы рассматриваем Height Map ландшафт - ландшафт, сгенерированный из текущей карты высот.

#define AREA_SIZE    128             /* размер карты */
#define F            16.0            /* scale величина масштабирования карты */

float              height_field[AREA_SIZE][AREA_SIZE];

// Function     : render_height_field
// Purpose      : рендеринг ландшафта.
//
void render_height_field( void )
{
    int x,z;

    glColor3f(0, 0.5, 0.1);         
    glBegin(GL_QUADS);
    for(x = 0; x < AREA_SIZE-1; x++)
    {
        for(z = 0; z < AREA_SIZE-1; z++)
        {
            glVertex3f(F*(x+1),  F*height_field[x+1][z],    F*z);
            glVertex3f(F*x,      F*height_field[x][z],      F*z);
            glVertex3f(F*x,      F*height_field[x][z+1],    F*(z+1));
            glVertex3f(F*(x+1),  F*height_field[x+1][z+1],  F*(z+1));
        }
    }
    glEnd();
}

И пару чисто OpenGL понятий для увеличения скорости рендеринга:

1. Гораздо эффективнее рендерить ландшафт как quad strips (группой квадратов) или triangle strips (группой треугольников) чем как квадраты или треугольники по отдельности. Вам только нужно послать половину вершин на вывод OpenGL.

Rendering a grid using triangle strips

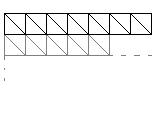
2. Использование OpenGL call list. Если ландшафт статический и не меняется,  OpenGL рендерит этот стек-список при рендеринге каждого фрейма. Если нет необходимости изменять данные вершин в этом call stack, то рендеринг с помощью его довольно эффективен.

Ниже представлен код, где ландшафт рендерится группой треугольников (triangle strips). Данные рендеринга компилирются в специальный стек, который достаточно один раз вызвать, чтобы прорендерить записанные в нем аершины. Вызов этого стека-списка производится постоянно при рендеринге. Это упрощенный код без текстурирования и расчета нормалей.

#define AREA_SIZE  128             /* размер карты */
#define F          16.0            /* scale величина ландшафта */

float              height_field[AREA_SIZE][AREA_SIZE];
int                step = 4;      // шаг рендеринга
GLuint             listid;        // GL идентификатор для вызова листа


// Function     : compile_height_field
// Purpose      : создает OpenGL call list для рендеринга карты высот
void compile_height_field( void )
{
    int x,z;

    listid=glGenLists(1);                               
    glNewList(listid,GL_COMPILE);               
    glColor3f(0, 0.5, 0.1);         
    glBegin(GL_TRIANGLE_STRIP);
    for(x = 0; x < AREA_SIZE-step; x+=step)
    {
        for(z = 0; z < AREA_SIZE-step; z+=step)
        {
            glVertex3f(F*(x+step), F*height_field[x+step][z], F*z);
            glVertex3f(F*x, F*height_field[x][z], F*z);
        }
    }
    glEnd();
    glEndList();    
}

// Function     : render_height_field
// Purpose      : Вызывает созданный в предыдущей функции стек вершин для рендеринга
void render_height_field( void )
{
    glCallList(listid);
}

Вот как это выглядит на практике:

Технология "Level of Detail"

При маленьких ландшафтов, составленных из относительно больших треугольников, техника, описанная здесь может удовлетворить все Ваши потребности, это будет лучшим решением и для скорости. Эта техника известна так же под названием "Полный рендеринг". Однако, если у нас ландшафт средних размеров или больших размеров, мы столкнемся с проблемами. Чем больше треугольников, тем более реалистично отображается рельеф. По мере возрастания размера ландшафта возрастает и количество треугольников, что приводит к тормозам.

 

Размер ландшафта	Количество треугольников
64x64	8,192
128x128	32,768
256x256	131,072
512x512	524,288
1024x1024	2,097,152

Однако, как нам справиться с рендерингом реалтайме, если при таком количестве треугольников компьютер тормозит? Выход - или иметь свермощный компьютер или использовать одну из Level of Detail технологий. Проще говоря, это означает, что области ландшафта высокой детализации нам нужны всего-лишь возле камеры, а дальше, за линией горизонта или еще дальше - нам совсем не нужна качественная детализация, ведь мы все равно не видем отдаленные области. В частях ландшафта, которые далеко от камеры можно использовать меньшее количество треугольников для рендеринга.

Некоторые LOD технологии:

• Lindstrom-Koller. Основан на сетке высот (размер карты+1) структурированной как квадродерево вершин.
• ROAM (Real-time Optimally Adapting Meshes). Использует прямоугольный треугольник, который делится на более маленькие треугольники. Этот метод использовал Seumas McNally в игре Treadmarks.
• Rottger et al. Квадродерево блоков ландшафта, записанное в матрицу.

В этой таблице приводится сравнение рендеринга с LOD и рендеринга без LOD .

 

	Размер карты 127x127	Размер карты 255x255
без LOD	83 fps / 32,258 triangles	30 fps / 130,050 triangles
c LOD	70 fps / 1,686 triangles	57 fps / 2,152 triangles

Тестировалось на Athlon 550 Mhz с видюхой Viper V770.

Почему так получается? Если посмотреть на код автора Nikolas Anderson (LOD исходники он убрал со своего сайта год назад, для полноты информации я выкладываю этот исходник здесь, однако в этом исходнике мало интерестного - ландшафт загружается не с карты высот а случайно генерится), вы заметите, что рендеринг идет вниз рекурсивно вглубь функцией draw которая вызывает OpenGL для вывода треугольников. Рекурсия делает код более удобным (Рекурсия - функция, которая вызывает сама себя) но иногда это может иметь затруднения в скорости работы. Marko Monster придумал две идеи для ускорения работы, основанных на том, что рекурсивная функция определяет набор треугольников. Рекурсия очень удобна для определения того, какие треугольники нужно рендерить. Так, разделим наш процесс на две части: 1) сначала мы определяем, какие треугольники должны рендериться для текущего состояния ландшафта, 2) а после уже рендерим их. Первый шаг мы делаем только при изменении позиции камеры, а второй шаг должен выполняться при каждом рендеринге фрейма.

Самый простой путь для этого - использование OpenGL display list. Определяем новый Vertex list вызывая рекурсивную функцию каждый раз при изменении положения камеры. После этого вызываем Display-Vertex list для каждого фрейма. Будет примерно так:

    listid=glGenLists(1);                               
    glNewList(listid,GL_COMPILE);  
    setup_quadtree( ... )                    
    glEndList();

Идея Marko Monster состоит в том, чтобы дать возможность рекурсивной функции записывать треугольники в специальный массив когда меняется положение камеры и рендерить треугольники при каждой прорисовке фрейма. Это похоже на первоначально предложенную идею с дисплейным списком, но в этом случае мы сами програмно создаем свой дисплейный список без помощи OpenGL library.

#define MAX_VERTS       30000

typedef struct NV
{
        VEC3    vertex;
        VEC3    normal;
} NV;

NV              nvertices[MAX_VERTS];
int             nverts =        0;

void init_nverts( void )
{
        nverts = 0;
}

static void add_nvert(x1, z1) 
{
         ASSERT(nverts <  MAX_VERTS);
        
         nvertices[nverts].vertex.x = F*x1;
         nvertices[nverts].vertex.y = F*height_field[x1][z1];
         nvertices[nverts].vertex.z = F*z1;
         
         nvertices[nverts].normal.x = normals1[x1][z1].x;
         nvertices[nverts].normal.y = normals1[x1][z1].y;
         nvertices[nverts].normal.z = normals1[x1][z1].z;

         nverts++;
}

static void do_triangle(int x1, int z1, int x2, int z2, int x3, int z3)
{
        add_nvert(x1, z1);
        add_nvert(x2, z2);
        add_nvert(x3, z3);
}

void spew_triangles( void )
{
        int     i;
        NV      *pv;

        pv = nvertices;  
        glBegin(GL_TRIANGLES); 
        for(i = 0;i<nverts;i++)           
        {
             glNormal3f(pv->normal.x,pv->normal.y,pv->normal.z);
             glVertex3f(pv->vertex.x,pv->vertex.y,pv->vertex.z);
             pv++;
        }
        glEnd();
        triangles_drawn += nverts/3;
}

После мы сделаем функцию генерирования треугольников так, чтобы она рендерила треугольники группой, примитивом Triangle fan вместо рендеринга треугольников по-отдельности. Эта OpenGL технология позволяет нам задать окружающие вершины треугольников, которые расположены вокруг основной центральной вершины - такая конструкция требует гораздо меньше памяти на вершины, к тому-же довольно быстро выводится на экран. Это образец примитива triangle fan, который задают 8 вершин, вместо 18 вершин, которые нужны для рендеринга такого же количества треугольников (6 соседних).

#define MAX_VERTS       30000

typedef struct NV
{
        VEC3    vertex;
        VEC3    normal;
} NV;

NV              nvertices[MAX_VERTS];
int             nverts = 0;

void init_nverts( void )
{
        nverts = 0;
}

// emit - вызывается чтобы записать вершину в vertex list
static void emit(x1, z1)
{
        ASSERT(nverts < MAX_VERTS);
        
         nvertices[nverts].vertex.x = F*x1;
         nvertices[nverts].vertex.y =  F*height_field[x1][z1];
         nvertices[nverts].vertex.z = F*z1; 
         nverts++; 
}

 // end - вызывается для закрытия Vertex list - закрытия triangle fan-а
static  void end(  void  )  
{
        nvertices[nverts].vertex.x = -9999; //(использует специальное число)
        nverts++; 
}

// рендериг Vertex List
void spew_fans( void ) 
{ 
        int i; 
        NV *pv;
        pv = nvertices; 
        glBegin(GL_TRIANGLE_FAN);

        for(i =  0;  i <  nverts; i++)
                {
            if(pv->vertex.x< = -9990)                
            {                        
                glEnd();                        
                glBegin(GL_TRIANGLE_FAN);                
            }
            else
            {
                glVertex3f(pv->vertex.x,pv->vertex.y,pv->vertex.z);
            }
            pv++;
        }
        glEnd();
}

• В Rоttger ROAM документации массив, хранящий данные деления квадродерева, используется того же самого размера как HeightMap карта высот. Причем используется совсем малая часть массива, хранящего данные деления квадродерева, остальная же часть не используется. Можно использовать более компактную технологию записи, которая сократит размер массива и позволит увеличить скорость.

• Когда меняется положение камеры, очень заметно резкое изменение детализации, что выглядит не очень хорошо, чтобы детализация менялась более плавно и незаметно, следует использовать технологию, называемую "Геоморфинг". Эта технология позволяет избежать резкого и грубого изменения детализации, заменяя его плавным.

• Текстурирование ландшафта. Возможно использование нескольких уровней текстуры: текстуры большого размера с альфа-прозрачностью совместно с детализацией другой текстуры в зависимости от расстояния. При этом придеться отказаться от нормалей и освещения реального времени, его можно заменить на заранее рассчитанное освещение для карты текстуры.

Surface roughness - фактор адаптивности (коофицент неровности)

Для отображения ландшафта ROAM алгоритму необходимо знать, где на ландшафте больше всего неровных поверхностей, чтобы покрыть их большим числом полигонов, а там где неровностей мало, ROAM тратит меньше полигонов на отображение такой области. Тут нам нужно знать, а как определить неровности на ландшафте? Здесь нам и поможет коофицент неровности. По HeightMap коофицент неровности рассчитывает для каждого квадрата сетки, чтобы впоследствии по этому коофиценту определять, сколько полигонов тратить на рендеринг конкретной области ландшафта.

Коофицент неровности так-же берется в расчет, когда мы принимаем решение о делении квадратов - узлов дерева. Использование коофицента неровности позволяет более точно отображать ландшафт. При движении камеры происходит изменение детализации ландшафта, а коофицент неровности позволяет более точно делить квадраты-области дерева для более точной визуализации.

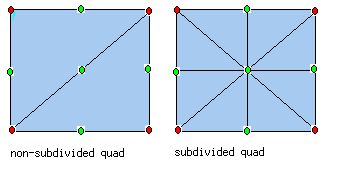
Коофицент неровности расчитывается заранее для каждой точки сетки высот,  значение коофицента неровности i-того квадрата влияет на критерий деления этого квадрата. Эта величина отражает на сколько ухабистый ландшафт в i-том квадрате и на сколько данная степень детализации соответствует рельефу конкретной области ландшафта. Соответственно, чем на большее количество квадратов - узлов поделена нужная область ландшафта, тем больше треугольников уйдет на эту область и тем более точно она будет отображена.

До деления квадрат имеет более низкую детализацию - вершины угла (красные) остаются те-же, но после деления квадрата на 4 дочерних высота (HeightMap) в зеленых вершинах будет отличаться от высоты в красных вершинах на некую величину interpolation errors (приближенная погрешность).

....

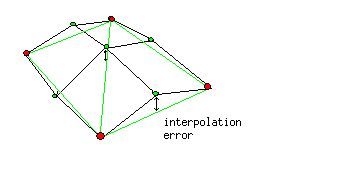
В Rottger ROAM документации коофицент неровности назван как d2 и это значение рассчитывается для каждой точки ландшафта. На самом низком уровне (3x3 квадрата) это максимальное значение приближенной погрешности (interpolation errors), которое мы получаем если не учитывать вершину в центре края. D2 коофицент неровности показывает на сколько неровен ландшафт в пределах квадрата - чем больше значение D2, тем неровнее ландшафт и тем больше полигонов нужно затратить на данный квадрат. При высоком уровне детализации значение d2 данного квадрата берется как максимальное значение d2 нашего квадрата и соседних квадратов. При высокой детализации мы учитываем значения коофицента неровности соседних квадратов для того, чтобы не было разрывов в сетке ландшафта.

К примеру у нас два квадрата - в первом квадрате значение d2 велико (значит велика ухабистость ландшафта в этом квадрате), а во втором квадрате d2 маленькое (рельеф более ровный). Если при такой ситуации мы разделим квадрат с большим значением d2, а соседний квадрат оставим без деления - то при рендеринге у нас получится "нестыковка" соседних квадратов. Чтобы этого не было, при вычислении коофицента неровности второго квадрата с несложным рельефом мы берем максимальное из двух d2 значений соседних квадратов - первого и второго.

Расчет d2 значения описан в этой статье, но этот метод не претендует на универсальность, есть много альтернативных решений.

Расчет начинается с начала - с вычисления 3x3 квадрата и заканчивается на 512x512 квадратах. Сначала вычисляется d2 конкретного квадрата, после вычисляется максимальное значение текущего квадрата и соседних.

Опишу подробно методику расчета d2 значения.

Это значение рассчитывается на этапе инициализции приложения. Для начала поясню, что такое HeightError.

Вычисление HeightError

Представь себе квадрат. Мы перебираем каждое ребро квадрата (всего 4 ребра) и две диагонали.
Берем 2 угла квадрата (иными словами начало и конец ребра или диагонали).
Вычисляем высоту (по heightmap) в этих двух углах - это переменные h1 и h2 в функции AddHError.
Далее вычисляем значение реальной высоты Height Map в точке середины ребра - переменная h_mid.
Дальше, по высоте 2 углов (начала и конца ребра) мы находим среднюю арифметическую высоту между ними - высоту ребра (h1+h2)/2.0f.

Таким образом, у нас  есть 4 величины высоты -
1). Начало ребра h1
2). Конец ребра h2
3). Высота в точке середины ребра, найденная путем среднего арифметического между высотами точек начала и конца ребра. (h1+h2)/2.0f
4). Реальная высота в середине ребра по Height Map - h_mid.

Далее, из реальной высоты вычитаем высоту, полученную как среднее арифместическое.
Получаем разницу между реальной и средней высотами в середине ребра - это и есть HeightError.
height_error = h_mid - (h1+h2)/2.0f;

Так обрабатываются все 4 ребра и две диагонали - функция AddHError вызывается из функции calc_roughness 6 раз.

Таким образом, находим такую разность для каждого ребра квадрата и 2 диагоналей. Потом, берем самую максимальну из них

if(height_error > *pmax_error) *pmax_error = height_error;

и делим на длину ребра квадрата - это и есть roughness фактор для i-того квадрата.
RFactor = (mxError / EdgeLenght);

Теперь, как это выглядит в реале.

void ROAM::AddHError( int xmin, int zmin, int xmax, int zmax,
       float *pmax_error )
{
 float h1, h2;
 float h_mid;
 float height_error;

 // height at 2 corner vertices
 h1 = HT(xmin, zmin);
 h2 = HT(xmax, zmax);

 // height at middle of edge or in middle of diagonal
 // (=halfway between the two corners)
 h_mid = HT((xmin+xmax)/2, (zmin+zmax)/2);

 // height error caused by interpolation between corner vertices
 height_error = h_mid - (h1+h2)/2.0f;

 if(height_error > *pmax_error)
  *pmax_error = height_error;
}

void calc_roughness( void )
{
 int  level; // level of detail
 int  edge_length;
 float max_error;
 float d2;
 int  x,z;

// я эту переменную не использовал
 K = MINIMUM_GLOBAL_RESOLUTION / (2.0f*(MINIMUM_GLOBAL_RESOLUTION-2.0f));

 level = 1; // lowest level: quads of 3x3
 edge_length = 2;

while( edge_length <= AREA_SIZE )  // loop from detailed scale to top level scale
 {
  for( x = level; x < AREA_SIZE; x+=edge_length )
  {
   for( z = level; z < AREA_SIZE; z+=edge_length )
   {
    max_error = 0;
    //передаем координаты первого ребра для вычисления его HeightError
    add_height_error(x-level, z-level, x-level, z+level, &max_error);
    //передаем координаты второго ребра ребра
    add_height_error(x+level, z-level, x+level, z+level, &max_error);
    //передаем координаты третьего ребра ребра
    add_height_error(x-level, z-level, x+level, z-level, &max_error);
    //передаем координаты четвертого ребра
    add_height_error(x-level, z+level, x+level, z+level, &max_error);
    //координаты первой диагонали
    add_height_error(x-level, z-level, x+level, z+level, &max_error);
    //координаты второй диагонали
    add_height_error(x-level, z+level, x+level, z-level, &max_error);

    //roughness фактор=максимальный HeightError/длину ребра
    d2 = max_error / (float)edge_length;

/* если уровень детализации >1, то нам надо чтобы небыло surface break учитывать фактор адаптивности соседних квадратов. Если в соседнем квадрате фактор адаптивности больше данного, то за данный берем наибольший фактор адаптивности. */
    if( level > 1 ){
// максимальный фактор адаптивности между соседними квадратами по центру ребра
     d2 = MAX(d2, K * ROUGHNESS(x, z-level));
     d2 = MAX(d2, K * ROUGHNESS(x, z+level));
     d2 = MAX(d2, K * ROUGHNESS(x-level, z));
     d2 = MAX(d2, K * ROUGHNESS(x+level, z));
    }
// максимальный фактор адаптивности между соседними квадратами по центру квадрата и 4 углам квадрата.
    ROUGHNESS(x,z) = d2;
    ROUGHNESS(x-level,z-level) = MAX(d2, ROUGHNESS(x-level,z-level));
    ROUGHNESS(x-level,z+level) = MAX(d2, ROUGHNESS(x-level,z+level));
    ROUGHNESS(x+level,z+level) = MAX(d2, ROUGHNESS(x+level,z+level));
    ROUGHNESS(x+level,z-level) = MAX(d2, ROUGHNESS(x+level,z-level));
   } // for z
  } // for x

  level *= 2;
  edge_length *= 2;
 }
}

Мы сравниваем коофицент неровности с соседним квадратом по 4 точкам центра ребра и по 4 углам квадрата.

Так в цикле пробегаем каждый квадрат и записываем в массив фактор адаптивности каждого
квадрата. Дальше, в конце цикла увеличиваем квадрат и пробегаем все заново с большим размером квадрата и так далее (пробегаем по каждому уровню детализации) до достижения максимального размера квадрата - от 3х3 до 512х512.

Сначала находим дистанцию от камеры до центра квадрата. После чего, используя полученное значение d2 расчитываем значение f, которое является критерием деления квадрата:

                     
              L
f =     ------------------
       d * C * max(detailLevel*d2, 1 )

Если f получается больше или равным 1, тогда квадрат необходимо делить.
Привожу реализацию функции построения квадродерева

//X и Y передают ЦЕНТР квадрата
void ROAM::QTreeSetup(int X, int Y, int Side)
{       
        float f;        
        //находим высоту в координатах X, Z центра нашего квадрата
        Height=(-hf(X,Y));
       
        //дистанция от камеры до центра квадрата
        distance=fabs(X-location_x)+(fabs(Height-location_y))+fabs(Y-location_z);

        //на основе этого значения мы определяем, продолжать или прекращать
        //деление квадрата дерева на 4. Используеться roughness фактор
        f = (distance)/(Side * MIN_GLOB_RES * MAX(detailLevel*Roughness[X][Y]/3, 1.f ) );
        if (f<1.0f)
        {
                QT(X,Y)=NodePoint;
                // Рекурсивно делим квадрат на 4 квадрата
                if (!FrustumWorking(X, Y, Side)) {QT(X,Y) = 255; return;}// Frustum culling
                if (Side>1)
                {       // сторона каждого из новых 4 квадратов = исходная сторона/2
                        int HSide = Side / 2;
                        //рекурсивно вызываем функцию для деления квадрата на 4 новых. 
                        //При этом передаем параметр cullcode родительского квадрата
                        QTreeSetup(X-HSide, Y-HSide, HSide);
                        QTreeSetup(X+HSide, Y-HSide, HSide);
                        QTreeSetup(X-HSide, Y+HSide, HSide);
                        QTreeSetup(X+HSide, Y+HSide, HSide);
                }
                else QT(X,Y)=EdgePoint; // в дальнейшем квадрат неделим
        }
        else QT(X,Y)=EdgePoint; // в дальнейшем квадрат неделим
}

Чтобы не рассчитывать каждый раз заново d2 значения, их можно один раз сохранить в файл raw или bmp формата. Чтобы Вы лучше представляли себе, как "визуально выглядит d2, приведу 2 рисунка.
 

Это стандартная карта высот, по которой строится ландшафт.	А это массив d2 значений, рассчитанный для каждой точки карты и записанный в файл. Там, где белее точка - там значение d2 больше и больше неровности.

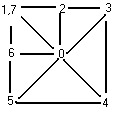
После функции построения квадродерева вызывается страшная на вид функция MakeMesh. Эта функция по построенному квадродереву (QT) строит лист вершин для каждого уровня детализации для последующего рендеринга вершин. По сути дела эта функция формирует конечный mesh на рендеринг. Вот фрагмент из этой функции.

// если центр квадрата в точке x-HWidth,z-HWidth равен значению EdgePoint
// то формируем соответствующий список вершин Triangle fan на рендеринг.

if(QT(x-HWidth,z-HWidth) == EdgePoint)
 {
  Emit(x-Width,z-Width);  // включаем соответствующую вершину в стек рендеринга
  Emit(x,z-Width);        // включаем соответствующую вершину в стек рендеринга
  End();                  // закрываем стек
  Emit(x,z);              // открываем новый стек
 }

Таким образом функция рекурсивно обходит все квадраты и в зависимости от значения QT в конкретном квадрате строится веер треугольников. То есть, берем 4 квадрата и в каждом формируем TRIANGLE_FAN в зависимости от значения QT(x,z)в конкретной точке.

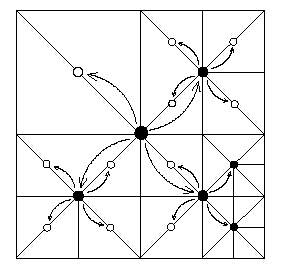
Дальше, каждый из этих 4 квадратов делим на 4 и так далее.
 

Frustum culling

Квадродерево очень подходит для frustum culling теста. Frustum culling - отсечение невидимых областей ландшафта при рендеринге, которые находятся за пределами раструба камеры.

Все это работает следующим образом. Берем один из 4 квадратов - узел квадродерева. Проверяем его на предмет попадания в камеру. Если он не попал в камеру - не делим квадрат на потомки и автоматически переходим к следующему из 4 квадратов.

if (!FrustumWorking(X, Y, Side)) {QT(X,Y) = 255; return;}

Если квадрат попал в камеру, хорошо, продолжаем его делить и проверяем каждый из 4 его потомков на предмет попадания в камеру, процесс повторяется до конца рекурсии - достижения последнего неделимого узла. Чтобы проверить, попадает ли квадрат в камеру, описываем вокруг квадрата воображаемый ограничивающий куб, берем каждую из 8 вершин этого куба и проверяем ее, если вершина ограничивающего куба попала в камеру, значит квадрат видим. Это объяснено очень упрощенно. Чтобы понять все детально, изучаете исходник. На самом деле, можно не проверять все 8 вершин куба. Если у нашего куба его длина равна ширине, то нам достаточно взять 2 вершины диагонали куба - минимальную нижнюю вершину и максимальную верхнюю вершину.

if (!FrustumWorking(X, Y, Side)) {QT(X,Y) = 255; return;}
 

Следующая диаграмма илюстрирует два уровня детализации отсечения. Красная линия это левая и правая отсекающие плоскости камеры. Серые квадраты находятся вне камеры, зеленые квадраты располагаются внутри камеры а голубые находятся частично в области видимости камеры - их мы рендерим.

Тест видимости frustum culling включен в функцию построения квадродерева.

Frustum содержит 6 ограничивающих плоскостей. Каждую плоскость можно представить уравнением плоскости

x*A + y*B + z*C + D = 0

Если в это выражение больше или равно нулю, то вершина находится в области видимости камеры - попадает в одну из плоскостей отсечения камеры.

Обратите внимание - мы во frustum culling передаем только координаты центра узла и длину его ребра, а 8 вершин ограничивающего куба и попадание их в камеру определяет функция FrustumWorking.

bool ROAM::FrustumWorking(int X, int Y, int Side)
{
 bbox.min[0] = (X*ScaleXZ)-(Side*ScaleXZ);
 bbox.min[1] = (Y*ScaleXZ)-(Side*ScaleXZ);
 bbox.min[2] = 0;

 bbox.max[0] = (X*ScaleXZ)+(Side*ScaleXZ);
 bbox.max[1] = (Y*ScaleXZ)+(Side*ScaleXZ);
 bbox.max[2] = iznanka*255;

 if (!g_Frustum.RightParallelepipedInFrustum(bbox.min, bbox.max)) return false;
 return true;
}

В структуру bbox мы записываем минимальную нижнюю вершину и максимальную верхнюю вершину ограничивающего куба. Обратие внимание, при  составлении bounding box квадрата мы берем реальные X и Z координаты квадрата, а вместо того, чтобы взять реальную Y координату мы берем минимальное и максимальное значение высоты ландшафта - 0 и 255, в bounding box идут только X и Z координаты узла, а вместо Z координат идут значения 0 и 255.

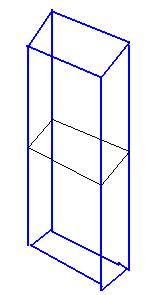
Рисунок для пояснения. Черный пунктир - это квадрат дерева. Синий паралелепипед, это bounding box, который описывает квадрат для frustum culling. Обратите внимание, что bounding box точно описывает квадрат только по левой, правой, передней и задней граням. А по вехней и нижней грани берется максимальная высота. Это особенность frustum culling-а в ROAM ландшафтах. Можно конечно попытаться точно описать bounding box-ом квадрат еще и по верхней и нижней грани впритык, но в этом случае frustum culling работает некорректно.

Далее вызываем функцию проверки попадания в область видимости.

bool CFrustum::RightParallelepipedInFrustum(float Min[3], float Max[3])
{
 unsigned int i;//CurPlane

 for (i = 0; i<6; i++)// пробегаемся по каждой из 6 плоскостей камеры.
 {
  if (Frustum[i][0]*Min[0]+Frustum[i][1]*Max[1]+Frustum[i][2]*Min[2]+Frustum[i][3]>0) continue;
  // уравнение плоскости для каждой из 8 точек ограничивающего куба
  if (Frustum[i][0]*Min[0]+Frustum[i][1]*Max[1]+Frustum[i][2]*Max[2]+Frustum[i][3]>0) continue;
  if (Frustum[i][0]*Max[0]+Frustum[i][1]*Max[1]+Frustum[i][2]*Max[2]+Frustum[i][3]>0) continue;
  if (Frustum[i][0]*Max[0]+Frustum[i][1]*Max[1]+Frustum[i][2]*Min[2]+Frustum[i][3]>0) continue;
  // если больше 0, то точка попала в одну из 6 плоскостей камеры
  if (Frustum[i][0]*Max[0]+Frustum[i][1]*Min[1]+Frustum[i][2]*Min[2]+Frustum[i][3]>0) continue;
  if (Frustum[i][0]*Max[0]+Frustum[i][1]*Min[1]+Frustum[i][2]*Max[2]+Frustum[i][3]>0) continue;
  if (Frustum[i][0]*Min[0]+Frustum[i][1]*Min[1]+Frustum[i][2]*Max[2]+Frustum[i][3]>0) continue;
  if (Frustum[i][0]*Min[0]+Frustum[i][1]*Min[1]+Frustum[i][2]*Min[2]+Frustum[i][3]>0) continue;
  return false;
 }
 return true;
}

Камера содержит 6 плоскостей - передняя, задняя, правая, левая, верхняя, нижняя - своеобразная усеченная пирамида.

Но это еще не все. В содержиться Frustum информация о плоскостях камеры. Эта структура должна постоянно обновляться - ведь камера движеться и координаты плоскостей постоянно меняются при движении камеры. Для этого мы постоянно вызываем функцию извлечения плоскостей - UpdateFrustum(). Для большинства исходников она стандартная, ее не надо каждый раз выдумывать заново.

Следующая таблица показывает результаты frustum culling когда камера расположена в центре карты высот 512x512.
 

Frustum Culling

	количество треугольников	количество triangle fans	fps
без frustum culling	2500	450	141
с frustum culling	500	150	141

И в заключении. Чтобы понять эту технологию, Вам придется приложить не мало усилий. Необходимо изучать исходник вместе со статьей. Я хотел разложить все предельно подробно в этой статье, но к сожалению у меня для этого не хватило времени. По этому я описал лишь основные моменты. В этой статье и исходнике по причине нехватки времени мне так и не удалось реализовать проверку столкновений. Вы можете попытаться сделать это сами, используя эту русскую статью с примером
http://gamemaker.webservis.ru/articles/Pick/Pick.htm
Так-же в этой Rottger ROAM технологии мне не удалось реализовать Geomorfing технологию. По правде говоря, сколько народу работало с Rottger ROAM, никому не удалось реализовать правильный геоморфинг - ни C. Cookson-у, ни Marco Monster-у. Я не стал зацикливаться на геоморфинге, а перешел к изучению более продвинутой ROAM технологии (на мой взгляд). В этой русской статье с примером данная технология представлена.
http://gamemaker.webservis.ru/articles/roam2/note.html
Я не стал в этой статье рассматривать Geomorfing (зачем, если нет его работающей практической реализации), а рассмотрел более плотно ряд других моментов. Если все-же Вам интерестна реализация геоморфинга в этой технологии, смотрите первоисточник этой статьи
http://home.planet.nl/~monstrous/terrain.html
У Marco Monster есть пример, где геоморфинг реализован, но довольно коряво
( http://home.planet.nl/~monstrous/dl/terr05c.zip) - вместе с этим ему пришлось ограничить работу LOD - изменение детализации при этом работает только при перемещении камеры по горизонтали, а LOD должен работать как при перемещении камеры по горизонтали, так и при вертикальном полете.

Другие материалы

Рендеринг ландшафтов

The Virtual Terrain Project Крупный "ландшафтный центр", содержащий множество исходников и статей по рендерингу ландшафтов. Однако по поиску очень неудобный сайт.

Real-Time Generation of Continuous Level of Detail for Height Fields
Первоисточник Rottger ROAM технологии - статья автора и исходник.

http://www.angelfire.com/scifi/myhome/xterra/
Пример реализации Rottger ROAM алгоритма

Willem H. de Boer, Fast Terrain Rendering Using Geometrical MipMapping, proposes a block-based LOD approach to make optimal use of 3d acceleration hardware and minimize cpu load

Real-Time, Continuous Level of Detail Rendering of Height Fields,
Lindstrom, Koller et al, Georgia Institute of Technology/SAIC
 

Terrain Generation utilities

Terragen. A comprehensive program to generate terrains and render them (non-realtime).

OpenGL Terrain Generator by Antonio Ramires Fernandes. It provides the Fault algorithm and the Circle algorithm, which are described in the tutorial on the same web site.

Автор оригинальной английской статьи
Marco Monster (Monstrous Software)
Перевод и дополнение Яценко Борис

НАЗАД