<При апробации теоретических основ призабойной пульсирующей промывки скважин, разработанных в ходе научных исследований первого автора, возникла дискуссия по поводу возможности использования приближенных значений начальных условий при численном интегрировании дифференциальных уравнений вместо точных нулевых значений скорости жидкости и координаты ее поверхности в вытеснительной камере механизма. Поясним суть вопроса. При расчете подачи погружного пульсационного вытеснителя использовался так называемый "энергетический подход", т.е. расчетная модель строилась на основании закона об изменении кинетической энергии системы. В полученных дифференциальных уравнениях при численном интегрировании нельзя использовать реальные начальные условия, т.е. при tB=0, х=0 и Y=0, где tB, x и Y соответственно время движения, координата и скорость жидкости, движущейся в вытеснительной камере. Например, на начальном этапе вытеснения жидкости, когда имеет место ламинарный режим течения, дифференциальное уравнение имеет вид:
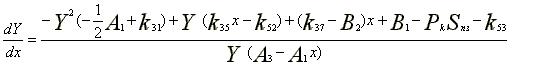
Расшифровка остальных параметров, входящих в (1), с целью сокращения объема настоящей статьи не приводится. Она приведена в [1, 2]. Для решения уравнения (1) начальные условия определялись приближенно, поскольку при подстановке нулевых начальных условий знаменатель правой части обращался в 0. Приближенные начальные условия определялись следующим образом. Для того чтобы решить (1) относительно Y (скорость течения жидкости) в зависимости от положения координаты ее свободной поверхности х в вытеснительной камере, необходимо на первом шаге интегрирования подставлять начальное значение Y при незначительном смещении свободной поверхности от начала координат. Предполагается, что в этом случае жидкость не успеет разогнаться до скорости, при которой будут существенны местные гидравлические сопротивления и сопротивления по длине. В результате было получено несложное дифференциальное уравнение движения жидкости, решение которого относительно Y позволи ло получить аналитическое выражение этого параметра при незначительном смещении свободной поверхности жидкости от начала координат, равном шагу интегрирования m.
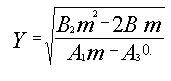
Значение Y, полученное из уравнения (2), и подставлялось вместо начального значения скорости жидкости на первом шаге интегрирования. Однако при обсуждении предложенной модели были высказаны сомнения в обоснованности такого подхода. Во-первых, действительно ли для предложенных уравнений незначительные изменения начальных условий не приводят к большим погрешностям при интегрировании. Во-вторых, можно ли при расчетах применительно к глубоким скважинам малого диаметра при больших давлениях рабочего агента пренебрегать гидравлическими сопротивлениями на начальных этапах движения жидкости.
Для устранения возможной некорректности, обусловленной использованием приближенных начальных условий, на основании уравнения Бернулли для неустановившегося движения жидкости была получена новая теоретическая модель призабойной пульсирующей промывки. В полученных дифференциальных уравнениях фигурируют первая и вторая производные по времени от координаты уровня жидкости в вытеснительной камере. Например, при описании начального этапа вытеснения жидкости при ламинарном режиме течения, дифференциальное уравнение имеет вид:
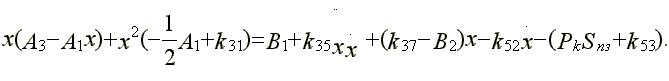
Уравнение (3) легко решается с использованием нулевых начальных условий (при tB=Q х=0 и x=0). Таким образом, мы получаем более точное решение дифференциального уравнения.
Авторами была проведена сравнительная оценка двух теоретических моделей призабойной пульсирующей промывки при бурении скважин. В табл. 1 и 2 приведены примеры результатов численного интегрирования уравнений для этапа вытеснения жидкости по первой и второй модели. При расчетах были приняты следующие значения параметров системы "буровой снаряд - скважина": внутренний диаметр вытеснительной камеры 0,098 м; наружный диаметр вытеснительной камеры 0,108 м; длина вытеснительной камеры 2 м; заглубление вытеснительной камеры под уровень жидкости 11м; глубина скважины 500 м; статический уровень жидкости в скважине 100 м; давление сжатого воздуха в вытеснительной камере 0,7 МПа. Параметры очистного агента: плотность жидкости 1010 кг/м3, структурная вязкость неньютоновской жидкости 0,005 Па·с, динамическое напряжение сдвига неньютоновской жидкости 1 Па. Подобные условия соответствуют глубокой скважине малого диаметра при больших давлениях рабочего агента.
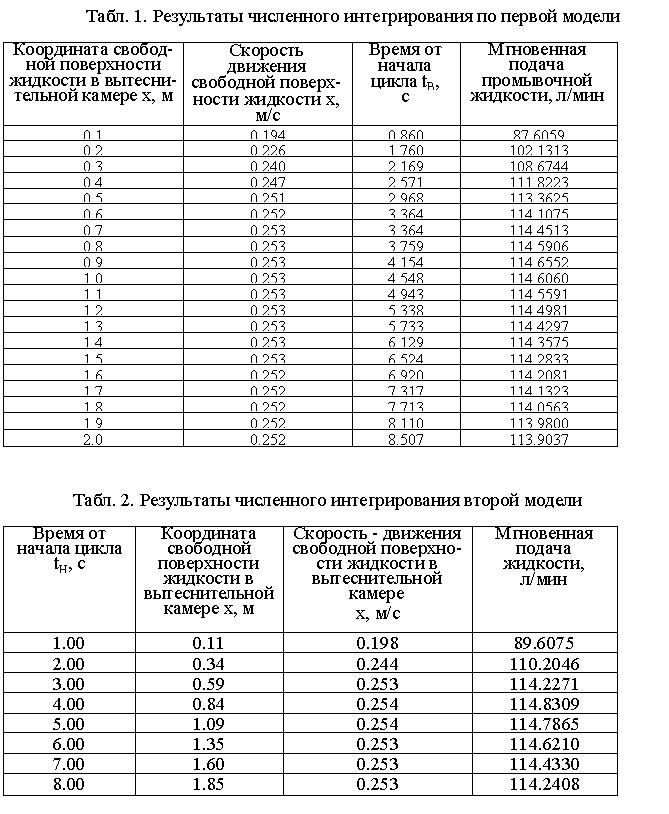
Таким образом, сравнительная оценка двух теоретических моделей призабойной пульсирующей промывки при бурении скважин показала их практическую идентичность с точки зрения точности полученных результатов. Поэтому для описания рабочих процессов в погружных пневматических вытеснителях могут применяться обе модели. Следовательно, результаты, полученные ранее при использовании первой модели, не теряют своего научного и практического значения.
- Филимоненко Н.Т., Комарь П.Л. К вопросу прогнозирования интенсивности призабойной пульсирующей промывки применительно к неньютоновской жидкости. // Совершенствование техники и технологии бурения скважин на твердые полезные ископаемые. Вып. 16. - Екатеринбург: УГИ, 1993. - С. 40 - 49.
- Филимоненко Н.Т Результаты исследования движения неньютоновской жидкости по инерции при работе пульсационного пневматического вытеснителя // Наукові праці Донецького дежавного технічного університету. Серія гірничо-геологічна. Вип.24. - Донецьк: ДонДТУ, 2001. - С.79 - 85.
-
©Филимоненко Н.Т., Каракозов А. А., Поцепаев В.В., 2002