Бинарные деревья представляют эффективный способ поиска. Бинарное дерево представляет собой структурированную коллекцию узлов. Деревья являются структурами несколько более сложными,чем списки. Списки представляются обычно, как нечто линейное, в то время как деревья в естественном представлении имеют более одного измерения. Деревья обычно изображают растущими сверху вниз, с корнем наверху. Отдельные ячейки, из которых составляется дерево, называют узлами ( или потомками ). Узел, имеющий дочерние узлы, называется их родительским узлом. Аналогия с генеалогическим деревом позволяет ввести термины прародитель, предок и потомок. Узел, не имеющий дочерних узлов, называется листом. Хотя узел может иметь более одного дочернего, родительский узел может быть у него только один. Структура данных, в которой узлы имеют более одного родителя, не может считаться деревом. Единственым узлом, не имеющим родителя является корневой узел. В двоичном дереве у узла может быть один, два или ни одного потомка. Дочерний узел, расположенный левее родительского, называется левым потомком ( левым дочерним ). Дочерний узел правее родителя называют правым потомком. Существенное свойство двоичного дерева - это то, что для каждого данного узла все узлы левее его ( т.е. левый дочерний и все его потомки ) содержат значения, меньше значения самого узла. Аналогичным образом все узлы правее данного содержат большие либо равные значения.

Левое поддерево поизвольной вершины X содержит ключи, не превосходящие key[X] ( значение вершины X ), правое - не меньшие key[X]. Разные бинарные деревья поиска могут представлять одно и то же множество. Время выполнения ( в худшем случае ) большинства операций пропорционально высоте дерева. При представлении с использованием указателей для каждой вершины дерева нужно хранить помимо значения ключа key и дополнительных данных, также и указатели left, right, parent (на левое и правое поддерево, а также родителя). Если ребёнка ( или родителя - для корня ) нет, соответствующая переменная должна равняться NULL. Ключи в двоичном дереве поиска хранятся с соблюдением свойства упорядоченности: Пусть X - произвольная вершина двоичного дерева поиска. Если вершина Y находится в левом поддереве вершины X, то key[X]>=key[Y]. Если вершина Y находится в правом поддереве вершины X, то key[X]<=key[Y] Типовые функции при работе с бинарным деревом. Функция печати выводит на экран все ключи, входящие в дерево. x - вершина бинарного дерева, left[x] - левое поддерево, right[x] - правое поддерево, key[x] - ключ, p[x] - родитель вершины. Печать(x) Начало 1 если x не равен NULL 2 тогда Печать(left[x]) 3 напечатать key[x] 4 Печать(right[x]) Конец Процедура поиска. Получает на вход искомый ключ k и указатель x на корень поддерева, в котором производится поиск. Она возвращает указатель на вершину с ключом k ( если такая есть ) или NULL ( если такой вершины нет ) Поиск(x,k) Начало 1 Пока x не равен NULL и k не равно key[x] 2 Начало 3 если k меньше key[x] 4 тогда x равно left[x] 5 иначе x равно right[x] 6 Конец 7 Вернуть x Конец Минимум и максимум. Минимальный ключ в дереве поиска можно найти, пройдя по указателям left от корня ( пока не дойдем до NULL ). Процедура возвращает указатель на минимальный элемент поддерева с корнем х. Минимум(x) Начало 1 Пока left[x] не равен NULL 2 Начало 3 x=left[x] 4 Конец 5 Вернуть x Конец Максимум(x) Начало 1 Пока right[x] не равен NULL 2 Начало 3 x=right[x] 4 Конец 5 Вернуть x Конец Данный принцип демонстрируется на рисунке.

При поиске ключа 13 мы идём от корня по пути 15->6->7->13. Чтобы найти минимальный ключ 2, мы всё время идём налево. Чтобы найти максимальный ключ 20 направо. Следующий и предыдущий элементы. Процедура возвращает указатель на следующий за x элемент или NULL в случае, если элемент x - последний в дереве. ПолучитьСледующийЭлемент(x) Начало 1 если right[x] не равен NULL 2 тогда вернуть Минимум(right[x]) 3 y равно p[x] 4 пока y не равно NULL и x равно right[x] 5 Начало 6 x равно y 7 y равно p[y] 8 Вернуть y Конец ПолучитьПредыдущийЭлемент(x) Начало 1 если left[x] не равен NULL 2 тогда вернуть Максимум(left[x]) 3 y равно p[x] 4 пока y не равно NULL и x равно left[x] 5 Начало 6 x равно y 7 y равно p[y] 8 Вернуть y Конец Добавление. Процедура добавляет заданный элемент в подходящее место дерево (такое место единственное), сохраняя свойство упорядоченности. Параметром процедуры является указатель z на новую вершину, в которую помещены значения key[z] ( добавляемое значение ключа), left[z]=NULL и right[z]=NULL. В ходе работы процедура меняет дерево T и возможно некоторые поля вершины z, после чего новая вершина c данным значением ключа оказывается вставленной в подходящее место (см. рисунок). Вставка(T,z) Начало 1 y равно NULL 2 x равно root[T] 3 пока x не равно NULL 4 Начало 5 y равно x 6 если key[z] меньше key[x] 7 тогда x равно left[x] 8 иначе x равно right[x] 9 Конец 10 p[z] равно y 11 если y равно NULL 12 тогда root[T] равно z 13 иначе если key[z] меньше key[y] 14 тогда left[y] равно z 15 иначе right[y] равно z 16 Конец
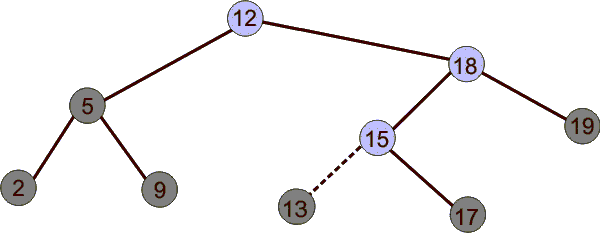
Удаление.
Параметром процедуры удаления явяляется указатель на удаляемую вершину. При удалении возможны случаи, указанные на рисунке ниже. Если у z нет детей, для удаления z достаточно поместить NULL в соответствующее поле его родителя ( вместо z ). Если у z есть один ребёнок, можно вырезать z, соединив его родителя напрямую с ребенком. Если же детей двое, требуются некоторые приготовления: мы находим следующий ( в смысле порядка на ключах) за z элемент y; у него нет левого ребёнка. Теперь можно скопировать ключ и дополнительные данные из вершины y в вершину z, а саму вершину y удалить описанным образом.

Удаление(T,z) Начало 1 если left[z] равно NULL или right[z]=NULL 2 тогда y равно z 3 иначе y равно ПолучитьСледующийЭлемент(z) 4 если left[y] не равно NULL 5 тогда x равно left[y] 6 иначе x равно right[y] 7 если x не равно NULL 8 тогда p[x] равно p[y] 9 10 если p[y] равно NULL 11 тогда root[T] равно x 12 иначе если y равно left[p[y]] 13 тогда left[p[y]] равно x 14 иначе right[p[y]] равно x 15 если y не равен z 16 тогда key[z] равно key[y] 17 // Копируем дополнительные данные связанные с y 18 Удалить y Конец