В работе рассматривается применение генетических алгоритмов для ситеза структур вычислительных систем реального времени (ВС РВ). Основное внимание уделяется проблемам настройки алгоритмов на задачу синтеза структур ВС РВ и обоснованию принятых решений, а также приводятся результаты статистического исследования алгоритмов. К основным проблемам, которые должны быть решены при настройке алгоритмов, можно отнести:
" кодирование сруктуры ВС и привязки процессов к процессорам. Выбранный способ кодирования должен обеспечивать возможность простого и однозначного вычисления целевой функции (критерия/функции выживаемости) и критерия останова, т.е. возможность однозначной и простой интерпретации функционирования ВС по соответствующей битовой строке; " выбор механизма селекции; " возможность обнаружения и исключения/коррекции недопустимых вариантов решения; " настройка критерия выживаемости и критерия останова; " уменьшение сложности операции мутации из-за большой длины битовой строки; " выбор начальной популяции; " выбор обьема популяции.
Рассмотрим генетический алгоритм для решения задачи приведенной ниже. Данный алгоритм будем называть базовым. Далее рассмотрим возможность применения базового алгоритма для решения задач синтеза структур в других постановках.
Для заданных:
" прикладной программы в виде наиболее сложной истории ее поведения H(A) = (P, ), где P- частично-упорядоченное множество рабочих интервалов/процессов, составляющих историю, - отношение частичного порядка на P;
" директивного срока ее выполнения (Tdir);
требуется определить:
" M - число процессоров в ВС,
" SP = {SPi}i=(1...M) - привязку процессов, составляющих программу, к процессорам ВС (SPi - упорядоченный список процессов, выполняемых на i-ом процессоре);
" IOM M - интенсивность межпроцессорного взаимодействия в форме матрицы интенсивности обменов между процессорами или временной диаграммы обменов;
при этом должны выполняться условия:
1) время выполнения алгоритма не должно превышать директивный срок Twa Tdir;
2) число процессоров M в ВС должно быть минимально необходимым для выполнения условия 1.
Разработанный алгоритм базируется на алгоритме предложенном Холландом и называемом Simple Genetic Algorithm (SGA). SGA можно схематично описать:
Алгоритм синтеза ( )
[
задание начальной популяции;
вычисление критерия выживаемости
пока не достигнут критерий останова;
[
селекция;
скрещивание;
мутация;
вычисление критерия выживаемости;
]
]
Рассмотрим настройку данного алгоритма на решение поставленной задачи. Кодирование Для однозначного распределения процессов по процессорам, необходимо для каждого процесса pi иметь номер процессора, на котором он выполняется (Mi) и его порядковый номер на этом процессоре (Nmi). Кодировка ВС в виде битовой строки и была сделана исходя из этих соображений. Схематично выбранный способ кодирования может быть представлен следующим образом: <битовая строка> ( <битовое поле процесса>i) <битовое поле процесса> (<номер процессора: Mi> <приоритет процесса>)
Порядок выполнения процессов назначенных на один процессор определяется в ходе анализа динамики функционирования ВС c использованием списочных расписаний. Формируется список процессов готовых к выполненю (выполнены все предшественники), инициализация процессов из этого списка осуществляется в соответствии с их приоритетами.
Выбранный способ кодирования позволяет свести к минимуму появление недопустимых конфигураций в результате выполнения операций скрещивания и мутации. Недопустимые конфигурации для данной задачи могут возникать из-за: нарушения частичного порядка и получения несуществующего номера процессора.
При выбранной кодировке недопустимые конфигурации связанны лишь с представлением номера процессора. Идеальной является ситуация в которой число процессов равняется N=2C. В таком случае любой полученный номер является подходящим, в противном случае мы будем получать не существующие номера процессоров. Так как число занятых процессоров не превышает числа процессов, то можно изменить не существующие номера в незанятые процессоры среди свободных с корректными номерами. Критерии останова и выживаемости
По задаче поставленной в данной работе алгоритм должен заканчиваться при выполнении двух условий: 1) время выполнения алгоритма не должно превышать директивный срок Twa Tdir, 2) число процессоров M в ВС должно быть минимально необходимым для выполнения условия 1. Наибольший критерий выживаемости должна иметь конфигурация отвечающая наиболее полно этим двум требованиям. Пусть kt - коэффициент отвечающий за первую часть требований и kopt - коэффициент отвечающий за вторую часть требований. Введем критерий выживаемости для битовой строки как линейную комбинацию этих коэффициентов:
k = C1 kt + C2 kopt , C1 + C2 = 1
где C1 и C2 - весовые множители. Как показало статистическое исследование алгоритма, их выбор может оказывать очень сильное влияние на характеристики алгоритма и качество получаемых решений.
Коэффициенты kt и kopt нормируются в интервале 0< kt,ktopt <1 и вычисляются следующим образом:
т.е., если алгоритм выполняется за время меньшее или равное заданному, то kt обращается в единицу. Коэффициент kopt определяет насколько ВС на данном этапе близка к оптимальной по числу процессоров. Однако, априорно оптимальная ВС не известна, поэтому kopt вводится следующим образом:
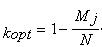
где N - максимальное число процессоров (полагается равным числу процессов N в алгоритме), Mj - число процессоров, использованных в данной конфигурации. Очевидно, что данный коэффициент никогда не обращается в единицу, также априорно не известно его максимальное значение.
В связи, с невозможностью априорной оценки критерия k для оптимального решения задачи, задание критерия останова также является проблематичным. Однако, для рассматриваемой постановки задачи всегда будет выполняться неравенство:
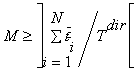(1)
где - округление до целого в большую сторону. Если алгоритм находит значение M для которого выполняется строгое равенство, то оно будет гарантированно оптимальным. Следует отметить, что варианта решения задачи для которого выполнятся строгое равенство в (1) может вообще не существовать.
Если алгоритм находит число процессоров, которое удовлетворяет строгому равенству в (1), то происходит его останов. В противном , алгоритм выполняется циклически, то есть задается начальный критерий выживаемости, а затем постепенно ужесточается. Когда алгоритм не сможет за заданное число итераций улутшить критерий выживаемости, то происходит его останов. В качестве "ужесточенного" критерия выживаемости берется наибольший в популяции и превышающий текущий критерий, если таков получен на очередной итерации.
Селекция
В алгоритме синтеза используются комбинация схемы пропорциональной селекции и схемы рулетки. Для вычисления целого числа потомков используется схема пропорциональной селекции, а для распределения остатка - схема рулетки.
Скрещивание
В алгоритме используется операция скрещивания SGA.
Мутация
В связи с большими объёмом битовой строки была модифицирована операция мутации. Вместо вызова генератора случайных чисел для каждого бита вычислялось случайным образом расстояние между инвертируемыми битами:
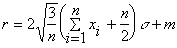
m=1/Pm - математическое ожидание,
Pm - вероятность мутации,
xi - равномерно распределённая (нормальное распределение) в промежутке [0, 1] случайная величина,
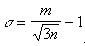- дисперсия.
Данное изменение сохраняет содержание операции, при этом её сложность снижается в 2 - 8 раз.
Разработанный алгоритм может быть использован для решения задач синтеза структур в других вариантах постановки лишь путем настройки его параметров и использованием соответствующих входных данных, без изменения его структукры. Рассмотрим настройку алгоритма на две наиболее часто встрещающихся на практике задачи:
1. Время выполнения прикладной программы должно быть минимально возможным, число процессоров в ВС при этом также должно быть минимально необходимым.
2. Время выполнения прикладной программы должно быть минимально возможным при заданном числе процессоров.
Минимально возможное время выполнения Tmin прикладной программы определяется критическим путем в графе H(A). При ограниченной арности вершин критический путь может быть найден за полиномиальное число шагов.
Разработаный алгоритм может быть использован для решения первой задачи без какой-либо настройки. В исходных данных алгоритму вместо Tdir задается Tmin.
Настройка алгоритма на вторую задачу осуществляется:
" ограничением при кодировке длины первого поля (<номер процессора>) в соответствии с заданным числом процессоров;
" заданием в исходных данных алгоритму вместо Tdir времени Tmin.
Аналогично разработанный алгоритм может быть настроен без каких-либо существенных изменений и на многие другие варианты постановки задач синтеза структур и планирования вычислений, а также и на более точные модели функционирования вычислительных систем.
Статистические испытания для "небольших" (десятки процессов) графов показали, что параметры разработанного алгоритма синтеза структур ВС могут быть настроены универсальным образом на характеристики графа H(A). При этом достигаются приемлемые сложность нахождения и качество решения. Оптимальное решение или достаточно близкое к нему находится за 50 500 итераций алгоритма. Наибольшее влияние на сложность получения и качество решения оказывают вероятность мутации и весовые коэффициенты (C1 и C2) в критерии выживаемости. Оптимальные параметры алгоритма находятся в пределах:
" размер популяции 25
" вероятность мутации 0.0075 0.0095
" вероятность скрещивания 0.3 0.5
" весовые коэффициенты (С1) 0.3 0.5
На число итераций алгоритма и качество получаемых решений оказывают сильное влияние следующие характеристики графа H(A): отклонение времен выполнения процессов, составляющих прикладную программу, от среднего значения (в данной работе рассматривались графы в которых отклонение от среднего не превышает 200 ) и степень связности графа H(A) (хоть и в меньшей мере).
Для более больших графов (сотни процессов) указанные выше закономерности проявляются аналогично.