В настоящее время шахты Донбасса осваивают добычу угля в лавах, глубина которых достигает 1000 и более метров, что влечет за собой повышение требований к четкости управления добычным оборудованием и соответственно к контролю технологических параметров.
Основное оборудование современного комплексно-механизированного забоя – это добычной комбайн, гидравлическая крепь и забойный конвейер.
Механизированные гидрофицированные крепи являются тем средством, которое обеспечивает упругий контакт между породами кровли и крепью и требуемую податливость стоек в процессе движения пород в выработанном пространстве. Требуемая податливость стоек крепи осуществляется путем вытеснения рабочей жидкости через предохранительный клапан при достижении установленного значения давления в рабочей полости стойки, обусловленного опусканием пород кровли.
При тяжелых горно-геологических условиях указанный принцип обеспечения податливости стоек крепи приводит к явлению задавливания гидростоек в процессе угледобычи.
С целью предотвращения упомянутого явления проводился анализ процесса опускания кровли, а под его действием опускания верхнего перекрытия крепи на одном шаге передвижки, что позволило бы в дальнейшем осуществить правильный контроль этого процесса и дальнейшее прогнозирование во избежание задавливания.
Для этого рассматривались осциллограммы опускания секций крепи для целого ряда секций механизированного комплекса. На рис.1 приведен вид таких осциллограмм.

Опускание кровли в конкретной лаве при конкретной крепи не является в строгом смысле случайной величиной, оно есть результат вполне определенных геомеханических условий и процессов. Однако многообразие причин горно-геологического и горно-технического порядка, влияющих на опускание кровли, настолько велико, что не поддается даже примерному учету. Отсюда опускание кровли носит случайный характер. В связи с этим оно должно подвергаться статическому анализу и обработке.
Опускание перекрытия гидрокрепи является прямым следствием опускания кровли, следовательно, его следует считать случайным процессом и можно применить те же методы анализа и обработки.
В основе применения вероятностных и статистических методов при решении инженерных задач лежит представление реальных объектов в виде математических моделей.
Требования, которым должна удовлетворять математическая модель, чтобы обеспечить эффективность применения статистических методов для решения задач с использованием средств вычислительной техники следующие:
- модель должна учитывать все существенные в условиях поставленной задачи черты изучаемого объекта;
- сложность модели должна целиком определяться решаемой задачей;
- модель должна иметь вид, пригодный для применения статистических критериев;
- модель должна быть простой по сравнению с другими пригодными в данном случае.
Для определения вида зависимости величины опускания крепи от времени были взяты осциллограммы этого процесса и рассмотрены как ряд реализаций случайного процесса.
Учитывая вид осциллограмм и требования, указанные выше, в качестве аппроксимирующей зависимости может служить одно из следующих выражений:
 (1)
(1)
где: h – величина распора секций;
t – время;
ci – коэффициенты аппроксимации.
Чтобы определить наиболее приемлемый вид математической модели, определялись значения коэффициентов ci для всех случаев, записывались уравнения с полученными коэффициентами и сравнивались значения h, полученные по аппроксимирующему уравнению и экспериментальные значения.
Для определения коэффициентов аппроксимирующих выражений был применен метод наименьших квадратов.
При методе наименьших квадратов требования наилучшего согласования аппроксимирующей кривой и экспериментальных точек сводится к тому, что сумма квадратов отклонений экспериментальных точек от сглаживающей кривой обращалась в минимальную, т.е.
![]() (2)
(2)
Для случая линейного полинома применение этого метода будет выглядеть следующим образом:
![]() (3)
(3)
Дифференцируем его по c0 и по c1, получаем:
![]() (4)
(4)
Далее:
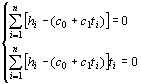 (5)
(5)
Выполнив определенные преобразования, находим статистические моменты:
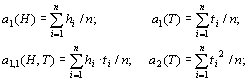 (6)
(6)
В результате получается система из 2-х уравнений:
![]() (7)
(7)
решая которую можем найти с0 и с1
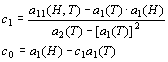 (8)
(8)
Аналогичным способом для полинома второй степени:
![]()
Получается система из 3-х уравнений:
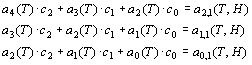 (9)
(9)
для решения которой использовался метод Крамера:
Аналогичным образом был проведен расчет для полинома 3-ей степени.
При рассмотрении функции
![]()
сначала выполнялось логарифмирование
![]()
Получалась система из 2-х уравнений:
 (10)
(10)
решая которую, получали выражение для определения коэффициентов
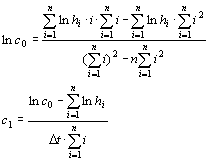 (11)
(11)
Статистические исследования проводились на 20-50 реализациях процесса, полученных для секций, расположенных внизу лавы, в нескольких местах вдоль лавы (20, 50, 70, 100, 120, 150 секции) и вверху лавы.
Коэффициенты модели были рассчитаны на ЭВМ с помощью программы, написанной на языке Pascal, и проверены с помощью функции Polyfit из библиотеки стандартных функций пакета Matlab.
Точность аппроксимации определялась по формуле:
![]() (12)
(12)
и для проведенных аппроксимирующих функций имела значения:

Следовательно, наиболее приемлемым аппроксимирующим выражением следует считать уравнение экспоненциальной зависимости.
Литература.
- Взаимодействие механизированных крепей с кровлей/ А.А. Орлов, В.Ю. Сетков, С.Г. Баранов и др. – М.:Недра, 1976.-283 с.
- Е.С. Вентцель. Теория вероятностей. – М.:Наука, 1969.- 576 с.
- В.П. Дьяконов. Matlab: учебный курс. – СПб: Питер, 2001.-560 с.:ил.