Впровадження високовиробничих технічних засобів розвідки, геофізичних методів пошуків, залучення в розвідку великих родовищ призвело до такого стрімкого зростання геологічної інформації, що традиційні засоби нагромадження та обробки даних вступили в протиріччя з обмеженими ресурсами праці і часу. Також зростають вимоги промисловості до вірогідності розвідницьких даних і точності їхнього графічного відображення.
Об'єм вхідних даних, отриманих за допомогою геологорозвідки величезний: на шахтному полі від декількох десятків до кількох сотень свердловин, свердловина може перетинати понад тисячі пластів, серед них до 20 вугільних пластів. Таким чином, для того, щоб розрахувати координати точок перетинання пласту з віссю свердловини необхідно зробити розрахунок декількох сотень тисяч координат точок перетинання.
Гіпсометричні плани пластів – найбільш важливі геолого-геометричні документи, що одержують у результаті геометризації вугільних родовищ.
Здатність розвідницького буріння навіть на стадії детальної розвідки, дозволяє виявляти розривні порушення з амплітудою не менше 10 – 15 м. Порушення з меншою амплітудою розвідницькими роботами звичайно не виявляються. Тим часом спостереженнями і документацією встановлено, що до 80% усіх тектонічних порушень, зустрінутих у гірських виробітках діючих шахт Донецького басейну, мають амплітуду в зазначених межах.
Основні результати розвідки вугільних родовищ представляються на гіпсометричних планах пластів, що використовуються при підрахунку запасів, проектуванні, будівництві та експлуатації гірських підприємств. Точність і вірогідність гіпсометричних планів залежать не тільки від складності геологічної будівлі шахтного поля або ділянки, детальності і якості розвідницьких робіт, але і від точності визначення координат точок перетинання пластів із свердловинами і методики структурних побудов.
Побудова гіпсометричних планів - складне і трудомістке завдання, у котрім необхідно визначити, побудувати і грузнути в єдину геологічну концепцію велику кількість структурно-геометричних елементів - точок, ліній, кутів, оцінок, поверхонь.
На основі автоматизації процесів можливо використання найбільше досконалих математичних моделей і методів рішення завдань. Вирішення вище означених питань можливо за допомогою використання комп'ютеризованої підсистеми комплексної обробки у виробничому режимі великих об'ємів кількісної і якісної інформації, що дозволяє здійснювати її багатопланову і різноманітну обробку для всебічного і поглибленого аналізу геологічних даних.
При буравленні стовбурів більшості розвідницьких свердловин скривлюються. Якщо скривлення відбувається тільки у вертикальній площині, то говорять про зенітне скривлення, якщо ж свердловина скривлюється тільки в горизонтальній площині, то таке скривлення називають азимутальним. При свердлінні свердловин геологи-розвідники заносять дані інклінометрії (відстань до точки виміру азимутального та зенітного кутів) у “Справу свердловини”. На основі даних інклінометрії свердловини обчислюють координати точок її стовбура. Досі для кожного інтервалу інклінометричного виміру зенітні кути й азимути обчислюють як середні зі значень, отриманих у сусідніх точках зйомки, що не завжди відбиває правдиве положення.
Для побудови поверхні шару необхідно знати координати точок перетинання осі свердловини із шаром. Ці розрахунки робляться за даними инклінометрії (зенітний кут, азимутний кут і відстань, на якій зустрівся шар).
При існуючій методиці основні розрахунки осі прокладки свердловин виконуються по методу, у якому для кожного інтервалу інклінометричній зйомки зенітні кути θ й азимутні кути α обчислюються як середні зі значень, отриманих у сусідніх точках зйомки:
Xn = X0 + 
sin[0.5(θi + θi+1)] cos[0.5(αi + αi+1)], (1)
Yn = Y0 + sin[0.5(θ i + θi+1)] sin[0.5(α i + αi+1)], (2)
Zn = Z0 - cos[0.5(θ i + θi+1)] (3)
де Xn , Yn і Zn - координати точки свердловини;
X0 ,Y0 і Z0 - координати гирла свердловини;
li - інтервал інклінометрии;
θi і αi - зенітні й азимутальні кути осі свердловини в точках спостереження.
Використання таких розрахунків веде до значних погрішностей у визначенні просторового положення свердловини і незручні для розрахунків координат точок перетинання осі свердловини з зустрінутими породними шарами. При машинному розрахунку зручніше згадати, що вісь свердловини є просторової кривою. У цьому випадку координати обчислюються по наступних формулах :
Xi+1 = Xi+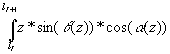
dz, (4)
Yi+1=Yi+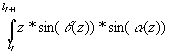
dz, (5)
Zi+1=Z-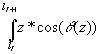
dz (6)
де i - індекс попередньої точки розрахунку,
i + 1 - індекс точки, у котрій необхідно обчислити координати.
По отриманих координатах необхідно змоделювати поверхню вугільного шару. Для обчислення інтегралів існують різні способи, але в нашому випадку їхня точність перевищує точність виміру азимутних і зенітних кутів. Тому можливо скористуватися формулою трапеції :
= (a-b){0.5[f(a) + f(b)] + 
i}/n, (7)
де n – число розбивок інтервалу інтегрування,
h =(b-a)/n ,
fi = f(xi) ,
xi = a + h* i, (i= 0,1,…,n)...
При обчисленні інтегралів необхідно знати значення підінтегральних функцій у точках між заданими значеннями. Обчислення цих значень можливо за допомогою інтерполяції.
Оскільки азимутні і зенітні кути вимірюються в довільно заданих точках осі свердловини можна скористатися так називаною інтерполяційною формулою. Однак у цьому випадку при обчисленні координат можлива поява великих помилок, оскільки не представляється можливим оцінити розмір залишкового члена поліному Лагранжа.
Інтерполяційним кубічним сплайном називається функція S(x), що володіє наступними властивостями :
- графік цієї функції проходить через кожну крапку заданого масиву,
S(x)=yi, i=0,1,...,m;
- на кожному з відрізків [xi, xi+1], i=0,1,...,m-1, функція є багаточленом третього ступеня,
- на усьому відрізку завдання [x0, xm] функція S(x) має безупинну другу похідну.
З математичної точки зору доведено, що вона є єдиною функцією, що володіє властивістю мінімальної кривизни, серед усіх функцій, що інтерполюють дані точки і мають другу похідну, що квадратично інтегрується . У цьому змісті кубічний сплайн є сама гладка з функцій, що інтерполюють задані точки.
Кубічний сплайн S має вигляд:
S(x)= w*yi+1 +v*yi +h
[(w3 – w)gi+1 + (v3- v)gi],
де х – незалежна перемінна ,
hi = xi+1 - xi,
w = (x – xi)/hi,
у- значення функції , що інтерполюються
v = 1 – w.
Невідомі коефіцієнти g повинні задовольняти системі рівнянь
=
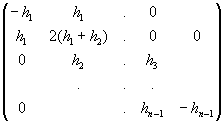
де: di = (yi-1 – yi)/(xi-1 – xi),
d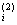
= (di+1 – di)/(xi+2 – xi),
d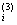
= (
)/(xi+3 – xi).
Цю систему рівнянь можна вирішити методом виключення.
Таким чином, послідовність формул, що представлено, дозволяє раціональним образом апроксимувати функціональною залежністю отримані в ході буравлення шпари значення координат точок з метою занесення їх у бази даних комп’ютерної системи.
Перелік джерел
- В.И. Кузьмін Побудова геологічних розрізів і гіпсометричних планів пластів. – М.: Надра, 1987.
- Ф.Преарата, М. Шеймос Обчислювальна геометрія: уведення. – М.: Світ, 1989. –478 с.