Исследование динамики цифровой системы управления курсом корабля

Червинская Н.В., Рафиков Г.Ш., к.т.н., доц. каф. АТ

Донецкий Национальный Технический Университет

Кафедра Автоматизированных систем управления

Abstract

Chervinskaya N.V., Rafikov G.S. Research of dynamics of a digital control system of the course of the ship.

In the article the results of the research of dynamics of a digital control system of the course of the ship are presented. The reactions of the system with different parameters upon the standard impacts are considered.

При экспериментальном моделировании часто необходим подробный анализ динамики параметров системы. Это связано с тем, что для многих систем незначительное изменение значений параметров в большую или меньшую сторону может привести к неустойчивому функционированию всей системы, а зачастую - к потере системой работоспособности. Этот анализ был выполнен для системы управления курсом корабля, структурная схема которой выглядит следующим образом:

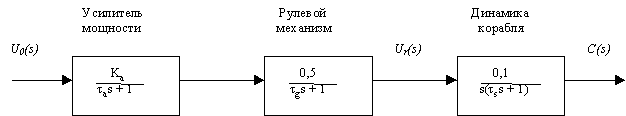
Рисунок 1. Общая структурная схема системы управления курсом корабля.

Усилитель мощности и рулевое колесо представлены моделями первого поряд-ка; динамика корабля представлена моделью второго порядка.

Было рассмотрено два варианта схем:- упрощенная система, пренебрегающая постоянной времени усилителя мощности; - и полная модель 4го порядка, учитываю-щая постоянную времени усилителя мощности tа.

Для первого варианта передаточная функция разомкнутой системы в общем виде выглядит следующим образом:

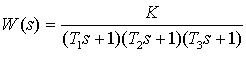
или для рассматриваемой системы:

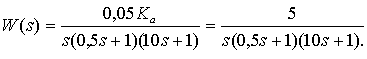
Перейдем к операторной форме записи. Получим выражение:

От операторной формы перешли к дифференциальной форме, а затем от диффе-ренциального уравнения 3-го порядка - к трем уравнениям 1го порядка. Сделаем замену:

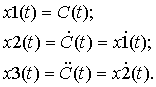
С учетом замены можно записать следующую систему:

К системе уравнений были применены методы матричной алгебры и получены уравнение состояния и уравнение выхода для непрерывной динамической системы.

Далее был осуществлен переход от непрерывной динамической системы к дискретной динамической системе. Для этого уравнение состояния и уравнение выхода представлено в следующем виде:

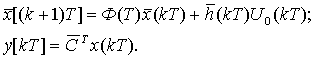
После нахождения матриц и определили условия достижимости, управляемости, наблюдаемости и восстанавливаемости ДДС.В нашем случае система оказалась достижима, управляема, наблюдаема и восстанавливаема.

Далее цель состояла в произведении синтеза матрицы обратной связи по состоя-нию модального регулятора на основе метода Аккермана:

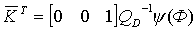
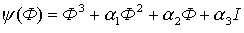
Рассчитали матрицу и получили матрицу коэффициентов обратной связи.

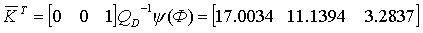
Исследования работоспособности синтезированного модального регулятора проводились в возмущенном режиме работы (при изменении параметров динамической системы K, T1, T2,T3 на ±20%, ±50%, ±100%). Для проведения исследований была разработана программа на языке пакета MATLAB, с помощью которой выполнялись рас-четы и были построены графики переходных процессов. Пример графика переходного процесса системы с регулятором и предварительным фильтром для номинальных значений коэффициентов К, Т1, Т2, Т3 приведен на рисунке 2

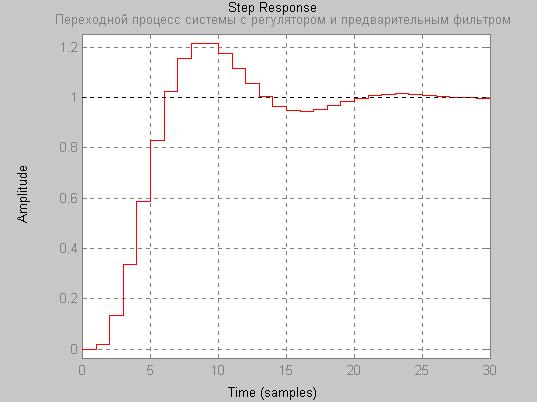
Рисунок 2. Переходный процесс системы с регулятором и предварительным фильтром.

Проведенные исследования позволили проанализировать влияние параметров системы на переходный процесс. Были получены следующие результаты:

Изменение параметра К на +20% и -20% не оказывает особого влияния на пере-ходный процесс. При изменении параметра К на +50% уменьшается перерегулирование системы, время нарастания остается прежним , а время переходного процесса сокращается. Реакция системы на линейно нарастающее воздействие существенно не меняется.

Изменение параметра Т1 на +20% увеличивает перерегулирование на 15% и время переходного процесса. Система становится менее стабильной. Изменение его на -20% существенного влияния не оказывает. Увеличение Т1 на 50% еще больше увеличивает перерегулирование (около 30%) и время переходного процесса. При увеличении данного параметра на 100% система существенно дестабилизируется, увеличивается время переходного процесса и перерегулирование на 45%, а также меняется реакция системы на линейно нарастающее воздействие, хотя существенных изменений не на-блюдается.

Изменение параметра Т2 на -20% и -50% не вносит существенных изменений в систему, а вот увеличение на 20% и 50% оказывает воздействие, аналогичное такому же изменению параметра Т1: время переходного процесса увеличивается, а перерегулирование достигает 40%. Таким образом, система дестабилизируется. Увеличение Т2 на 100% оказывает максимальное влияние на систему, т.к. система существенно дестаби-лизируется, время переходного процесса возрастает, а перерегулирование достигает 50%. Пример полученного графика переходного процесса системы с регулятором и предварительным фильтром при Т2=1(+100%) приведен на рисунке 3.

Рисунок 3. Обработка начальных условий системой с регулятором и предвари-тельным фильтром при Т2=1(+100%).

Изменение параметра Т3 на ±20% и -50% дало результаты, аналогичные измене-нию параметра Т1, т.е. не оказало существенного воздействия на систему - отклонения не превышали 10%. Существенное влияние на систему оказало изменение параметра на +50% и +100%.

Во втором варианте исследования системы учитывалась постоянная времени усилителя мощности, влияние которой оказалось незначительным.

Таким образом, можно сделать вывод, что проведенный анализ позволил иссле-довать динамику систему и оценить, как влияет на стабильность и устойчивость работы изменение её параметров. В результате исследования получили, что максимальное влияние на систему и ее переходные процессы оказывает параметр Т2, т.к. при его изменении на 100% время переходного процесса изменилось в 6 раз, перерегулирование достигло 50% и график реакции системы на линейно нарастающее воздействие получил искривление. То есть, для того, чтобы система была работоспособной и функционировала нормально, необходимо наиболее четко отслеживать изменение данного параметра.

Список источников

1.Современные системы управления/Р.Дорф, Р. Бишон. Пер. с англ. Б.И. Копы-лова.- М. Лаборатория Базовых Знаний, 2002. - 832 с.:ил.

2.Теорія автоматичного управління/Г.Ф. Зайцев, В.К.Степанов, О.І.Бріцький. За ред. Г.Ф.Зайцев - К.- Техніка, 2002.-688 с.