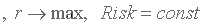Назад в библиотеку
Пономарев А.Ю.
Применение нечетких множеств для оценки риска портфельных инвестиций
http://journal.seun.ru/j2003_1r/Economy/economy.htm
Мировые фондовые рынки обладают существенным уровнем неопределенности, что влечет неустранимый риск, сопровождающий принятие инвестиционных решений. В ряде частных случаев традиционные методы анализа этого риска оказываются несостоятельными, так как они ориентируются на традиционный тип неопределенности, связанный с поведением однотипных объектов с неизменными свойствами. Связанные с такой неопределенностью риски сравнительно легко оцениваются на базе широко известных методов теории вероятностей. Однако в большинстве случаев фондовый рынок является ненадлежащим объектом для классического статистического исследования, так как объекты выборки из генеральной совокупности не обладают свойством статистической однородности, а случайные процессы не имеют постоянных параметров, так что никакие статистические гипотезы о виде указанных процессов подтверждены быть не могут.
Таким образом, борьба с неопределенностью на фондовом рынке обнаруживает свою бесперспективность, если такую борьбу вести традиционными способами. Необходимо кардинально менять подход к моделированию имеющейся информационной ситуации, а именно переходить от клаасической теории вероятностей к квазистатистике. Под квазистатистикой понимается выборка наблюдений из их генеральной совокупности, которая считается недостаточной для идентификации вероятностного закона распределения с точно определенными параметрами, но признается достаточной для того, чтобы с той или иной субъективной степенью достоверности обосновать закон наблюдений в вероятностной или любой иной форме, причем параметры этого закона будут заданы по специальным правилам, чтобы удовлетворить требуемой достоверности идентификации закона наблюдений. Применение квазистатистики дает расширенное понимание вероятностного закона, когда он имеет не только частотный, но и субъективно-аксиологический смысл. Здесь намечены контуры синтеза вероятности в классическом смысле - и вероятности, понимаемой как структурная характеристика основанная на знаниях эксперта.
Применение квазистатистики дает широкий простор для применения нечетких описаний для моделирования законов, по которым проявляется та или иная совокупность наблюдений. В терминах нечеткого описания от эксперта требуется не формирование точных значений оценки вероятностей, а задание расчетного коридора значений прогнозируемых параметров. Тогда ожидаемый эффект оценивается экспертом также как нечеткое число со своим расчетным разбросом. Здесь возникают инженерные преимущества метода, основанного на нечеткостях, т.к. эксперт оперирует не косвенными оценками, куда относятся и вероятности, а прямыми проектными данными о разбросе параметров, что является хорошо известной практикой интервального подхода к проектным оценкам.
Применяя нечетко-логические описания для задачи формирования фондового портфеля можно считать что доход по ценной бумаге (ЦБ) случаен, его точное значение в будущем неизвестно, а вероятностное описание такого сорта случайности не вполне корректно, то в качестве описания доходности ЦБ уместно использовать треугольные или трапецевидные нечеткие числа, моделируя экспертное высказывание следующего вида: "Доходность ЦБ по завершении срока владения ожидаемо равна 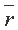 и находится в расчетном диапазоне
и находится в расчетном диапазоне 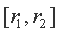 ". Здесь эксперт отказывается от вероятностного описания доходности, отсекает слабовозможные случайные исходы с двух сторон от ожидаемого значения
". Здесь эксперт отказывается от вероятностного описания доходности, отсекает слабовозможные случайные исходы с двух сторон от ожидаемого значения 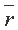 и формирует расчетный коридор, в котором ожидается уровень доходности ЦБ, при этом
и формирует расчетный коридор, в котором ожидается уровень доходности ЦБ, при этом 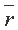 эксперт принимает либо наиболее ожидаемое, либо среднее значение доходности в расчетном коридоре. Функция принадлежности нечеткого числа имеет треугольный вид, если степень субъективной уверенности эксперта в отношении доходности равна нулю за пределами расчетного коридора значений доходности, а максимум этой уверенности, равный единице, достигается в точке
эксперт принимает либо наиболее ожидаемое, либо среднее значение доходности в расчетном коридоре. Функция принадлежности нечеткого числа имеет треугольный вид, если степень субъективной уверенности эксперта в отношении доходности равна нулю за пределами расчетного коридора значений доходности, а максимум этой уверенности, равный единице, достигается в точке 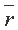 . Эксперт убежден, что
. Эксперт убежден, что 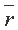 заведомо попадет в любой расчетный коридор доходности, как бы ни менялись границы этого коридора.
заведомо попадет в любой расчетный коридор доходности, как бы ни менялись границы этого коридора.
Если доходность ЦБ - треугольное нечеткое число, а доходность портфеля - линейная комбинация доходности компонент, то результирующий вид доходности портфеля также известен.
Пусть 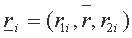 - доходность по i-ой ценной бумаге, треугольное нечеткое число. Тогда доходность по портфелю:
- доходность по i-ой ценной бумаге, треугольное нечеткое число. Тогда доходность по портфелю:
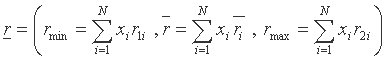
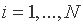
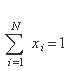 , где
, где 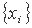 долевое ценовое распределением бумаг в портфеле,
долевое ценовое распределением бумаг в портфеле,
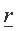 также является треугольным нечетким числом.
также является треугольным нечетким числом.
Теперь фиксируя 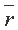 - требуемый уровень ожидаемой доходности портфеля и манипулируя вектором
- требуемый уровень ожидаемой доходности портфеля и манипулируя вектором 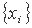 , можно добиться минимума риска инвестиций. Запись этой задачи:
, можно добиться минимума риска инвестиций. Запись этой задачи:
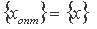 |
|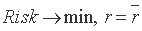
где 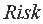 - функция степени риска неэффективности инвестиций, вычисляемая с использованием аппарата нечеткой математики.
- функция степени риска неэффективности инвестиций, вычисляемая с использованием аппарата нечеткой математики.
Эта задача является двойственной задачей нелинейного программирования к задаче в следующей записи:
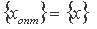 |
|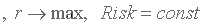
Эта задача подобна задаче Марковица, только в качестве фактора риска выступает не стандартное отклонение портфеля, а степень риска неэффективности инвестиций.
Применение нечетких множеств при учете исходной неопределенности относительно доходов по ценным бумагам - весьма перспективное направление анализа эффективности портфельных инвестиций. Эксперт-аналитик при использовании этого подхода избавлен от необходимости формировать вероятностные прогнозы на весьма шаткой информационной основе, когда поведение торгуемых ценных бумаг не обладает характером статистических случайных процессов. Эксперту достаточно сделать допущение о расчетном коридоре, в котором ожидаемо колеблется будущий доход по ЦБ. При этих простейших допущениях удается оценить степень риска неэффективности портфельных инвестиций и построить процедуру по минимизации этого риска.
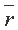 и находится в расчетном диапазоне
и находится в расчетном диапазоне 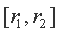 ". Здесь эксперт отказывается от вероятностного описания доходности, отсекает слабовозможные случайные исходы с двух сторон от ожидаемого значения
". Здесь эксперт отказывается от вероятностного описания доходности, отсекает слабовозможные случайные исходы с двух сторон от ожидаемого значения 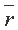 и формирует расчетный коридор, в котором ожидается уровень доходности ЦБ, при этом
и формирует расчетный коридор, в котором ожидается уровень доходности ЦБ, при этом 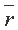 эксперт принимает либо наиболее ожидаемое, либо среднее значение доходности в расчетном коридоре. Функция принадлежности нечеткого числа имеет треугольный вид, если степень субъективной уверенности эксперта в отношении доходности равна нулю за пределами расчетного коридора значений доходности, а максимум этой уверенности, равный единице, достигается в точке
эксперт принимает либо наиболее ожидаемое, либо среднее значение доходности в расчетном коридоре. Функция принадлежности нечеткого числа имеет треугольный вид, если степень субъективной уверенности эксперта в отношении доходности равна нулю за пределами расчетного коридора значений доходности, а максимум этой уверенности, равный единице, достигается в точке 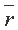 . Эксперт убежден, что
. Эксперт убежден, что 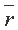 заведомо попадет в любой расчетный коридор доходности, как бы ни менялись границы этого коридора.
заведомо попадет в любой расчетный коридор доходности, как бы ни менялись границы этого коридора.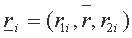 - доходность по i-ой ценной бумаге, треугольное нечеткое число. Тогда доходность по портфелю:
- доходность по i-ой ценной бумаге, треугольное нечеткое число. Тогда доходность по портфелю: 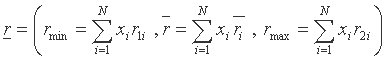
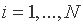
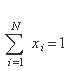 , где
, где 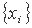 долевое ценовое распределением бумаг в портфеле,
долевое ценовое распределением бумаг в портфеле,
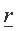 также является треугольным нечетким числом.
также является треугольным нечетким числом.
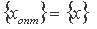 |
|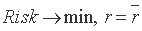
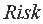 - функция степени риска неэффективности инвестиций, вычисляемая с использованием аппарата нечеткой математики.
- функция степени риска неэффективности инвестиций, вычисляемая с использованием аппарата нечеткой математики.