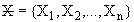 , где
, где 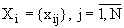 .
.Рассмотрим задачи обучения без учителя (или задачи самообучения, когда обучающая выборка отсутствует). Методы самообучения получили широкое распространение в интеллектуальных системах, в частности — в экспертных системах распознавания образов и классификации и т.д. В системах распознавания образов и классификации соответствующий класс задач обучения без учителя получил название кластер анализа (т.е. самопроизвольного разбиения исходной выборки на компактные полмножества, или кластеры).
Пусть задано множество наблюдений 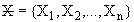 , где
, где 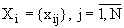 .
.
Требуется разбить выборку 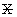 на непересекающиеся подмножества — кластеры
на непересекающиеся подмножества — кластеры 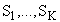 так, чтобы обеспечить минимум (экстремум) некоторого критерия (функционала качества), то есть:
так, чтобы обеспечить минимум (экстремум) некоторого критерия (функционала качества), то есть:
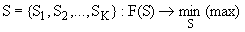
Если эти данные понимать как точки в признаковом пространстве, то задача кластерного анализа формулируется как выделение "сгущений точек" и разбиение исходной совокупности на однородные подмножества объектов. Кластерный анализ можно рассматривать также как метод редукции (сжатия) некоторого множества данных в более компактную классификацию объектов.
Рекомендуемая литература: [Айвазян с соавт., 1974; Миркин, Розенберг, 1978; Дюран, Оделл, 1980; Жамбю, 1988; Мандель, 1988].
Кластер определяется, как совокупность точек, лежащих на расстоянии не больше, чем r от некоторого "центра тяжести" в m–мерном пространстве (внутри гиперсферы радиуса r или гиперкуба со сторонами 2r).
В литературе описывается множество различных методов кластеризации, основанных на использовании матриц сходства, оценивании функций плотности статистического распределения, эвристических алгоритмах перебора, идеях математического программирования и др. Большая часть этих алгоритмов, при всей их несхожести, методически основаны на одной предпосылке — гипотезе компактности, т.е. "в используемом пространстве признаков измерения, принадлежащие одному и тому же классу, близки между собой, а измерения, принадлежащие разным классам хорошо разделимы друг от друга" [Кольцов, 1989].
Рассмотрим некоторые алгоритмы, основанные на использовании меры расстояния между объектами D. Введение метрики m–мерного пространства (т.е. способа оценки расстояний) является естественным приемом квантификации свойства схожести объектов: чем ближе между собой объекты в данной метрике, тем они более сходны и наоборот. Без этого само понятие "кластер" во многом теряет смысл, поэтому алгоритмы кластерного анализа часто формулируют в терминах дистанций.
Был предпринят ряд попыток разработать аксиоматический подход к введению метрических мер, согласно которым, например, расстоянием D называется двухместная действительная функция D(x1, x2), обладающая следующими свойствами:
Более конкретная математическая формулировка не имеет однозначного смысла, поскольку разные субъекты вкладывают в эту аксиоматику неодинаковое содержание.
Пусть мы имеем симметричную матрицу расстояний D между объектами исходной матрицы наблюдений:
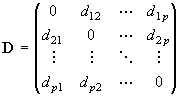
Компоненты матрицы D могут быть рассчитаны с использованием любой из концепций или формул (см. ниже), что не имеет значения для работы собственно алгоритмов таксономии.
Наиболее распространенную группу эвристических методов кластеризации составляют методы, основывающиеся на иерархической агломеративной процедуре (от латинского agglomero — присоединяю, накапливаю). Эти алгоритмы дают лишь условно–оптимальное решение в некотором подмножестве локальных разбиений (кластеров), однако достоинством этих методов является простота вычислений и интерпретации полученных результатов. Смысл иерархический агломеративной процедуры заключается в следующем. Перед началом кластеризации все объекты считаются отдельными кластерами, т.е. имеется p=n кластеров, каждый из которых включает по одному элементу. На первом шаге алгоритма определяются два наиболее близких или сходных объекта, которые объединяются в один кластер, общее количество которых сокращается на 1 (p:=p–1). Итеративный процесс повторяется, пока на последнем (р—1)–м шаге все классы не объединятся. На каждом последующем шаге агломеративной процедуры требуется пересчет лишь одной строки и одного столбца матрицы D, т.е. рассчитываются расстояния от образованного кластера до каждого из оставшихся кластеров.
Процедура иерархического кластерного анализа предусматривает возможность группировки как объектов (строк матрицы данных), так и переменных (столбцов). В последнем случае роль объектов кластеризации играют признаки исходной мадрицы:, например, виды гидробионтов.
Использовать построенную дендрограмму для выделения того или иного количества отдельных кластеров можно путем "разрезания" этой дендрограммы на определенном значении шкалы D. Фактически это означает, что мы проводим горизонтальную линию, рассекая дерево связей в том месте, где наблюдается максимальный скачок в изменении межкластерного расстояния.
Для определения расстояния между произвольной парой кластеров {Xi}, i=1,…k1 и {Yj}, j=1,…k2 с использованием различных версий алгоритмов классификации были сформулированы следующие подходы:
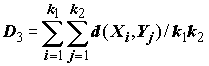 . (7.8)
. (7.8)Выделяется также совокупность методов, использующих статистические расстояния между кластерами (метод групповых средних, центроидный метод, метод Уорда и т.д.), где предполагается объединение, приводящее к минимизации суммы квадратов отклонений между каждым объектом и центром кластера, содержащим этот объект. Например, в методе Уорда [Ward, 1963] используется мера:
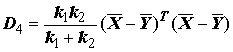 . (7.9)
. (7.9)Кроме иерархических методов классификации большое распространение получили также различные итерационные процедуры, которые пытаются найти наилучшее разбиение, ориентируясь на заданный критерий оптимизации, не строя при этом полного дерева. В начале последовательных итераций в качестве центра выбирается один из элементов и формируется кластер из элементов, удаленных от него не далее чем на r. Далее процедура повторяется для остальных элементов, причем в качестве очередного центра выбирается, например, "типическая" точка — лежащая на минимальном расстоянии от центра оставшегося множества объектов. После выполнения очередного шага выясняется, достигнуто ли желательное разбиение. Существуют различные методы определения критерия остановки процедуры:
На первом условии основывается наиболее популярный алгоритм — метод k–средних Мак–Кина [Фрей, 1967], в котором сам пользователь должен задать искомое число конечных кластеров, обозначаемое k. Принцип классификации заключается в следующем:
Наиболее важным свойством, используемым при анализе, является плотность распределения объектов внутри кластеров. Это свойство дает нам возможность определить кластер в виде скопления точек в многомерном пространстве, относительно более плотного по сравнению с иными областями этого пространства, которые либо вообще не содержат точек, либо содержат малое количество наблюдений. Несмотря на достаточную очевидность этого свойства, однозначного способа вычисления такого показателя плотности не существует. Наиболее удачным показателем, характеризующим компактность "упаковки" многомерных наблюдений в данном подмножестве, является дисперсия расстояния от центра кластера до отдельных его точек.
Другим примером критерия однородности может быть, например, функция, описанная А.А. Дорофеюком [1971]:
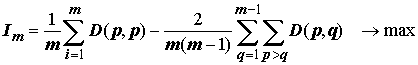 , (7.10)
, (7.10)значения которой подсчитываются для всех возможных вариантов разбиения исходного множества на m классов. В этой формуле D(p,p) — среднее сходство между собой всех векторов, попавших в одну группу, а D(p,q) — среднее сходство по всем парам векторов из разных групп p и q:
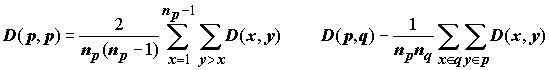 , (7.11)
, (7.11)где np и nq — число элементов в группах p и q.
Сохранено с http://www.tolcom.ru/kiril/Library/Book1/content373/
Возможны различные виды критериев (функционалов) разбиения множества на кластеры. Заметим, что эта задача тесно связана с определением некоторой метрики в пространстве признаков.
Рассмотрим наиболее широко используемые функционалы качества разбиения:
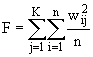 , (7.12)
, (7.12)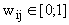 — некоторая степень принадлежности i–го объекта j–му кластеру. Диапазон изменения
— некоторая степень принадлежности i–го объекта j–му кластеру. Диапазон изменения 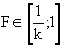 , где n — число объектов, K — число кластеров.
, где n — число объектов, K — число кластеров.
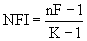 ,
, 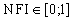 (7.13)
(7.13)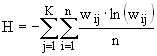 . (7.14)
. (7.14)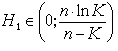 (7.15)
(7.15)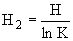 ,
, 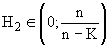 (7.16)
(7.16)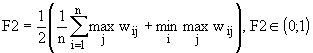 (7.17)
(7.17)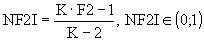 (7.18)
(7.18)Поскольку исходная информация задается в виде матрицы Х, то возникает проблема выбора метрики. Выбор метрики — наиболее важный фактор, влияющий на результаты кластер–анализа. В зависимости от типа признаков используются различные меры близости (метрики).
Пусть имеются образцы 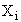 и
и 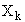 в N–мерном пространстве признаков.
в N–мерном пространстве признаков.
Основные метрики, используемые при кластеризации, приводятся в таблице 1.
| N | Наименование метрики | Тип признаков | Формула для оценки меры близости (метрики) |
|---|---|---|---|
| 1 | Эвклидово расстояние | Количественные | 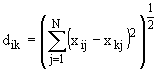 |
| 2 | Мера сходства Хэмминга | Номинальные (качественные) | 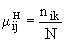 где 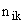 — число совпадающих признаков у образцов — число совпадающих признаков у образцов 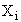 и и 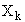
|
| 3 | Мера сходства Роджерса–Танимото | Номинальные шкалы | 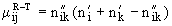 где 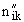 — число совпадающих единичных признаков у образцов — число совпадающих единичных признаков у образцов 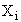 и и 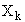 ; ;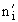 , , 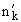 — общее число единичных признаков у образцов — общее число единичных признаков у образцов 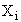 и и 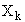 соответственно; соответственно;
|
| 4 | Манхэттенская метрика | Количественные | 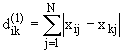 |
| 5 | Расстояние Махалонобиса | Количественные | 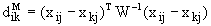 , ,где W — ковариационная матрица выборки; 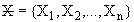 ; ;
|
| 6 | Расстояние Журавлева | Смешанные | 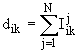 , ,где 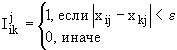
|
Существует большое число алгоритмов кластеризации, которые используют различные метрики и критерии разбиения. При этом число классов (кластеров) либо задается априори, либо определяется в процессе работы самого алгоритма.
Сохранено с http://www.i2.com.ua/index.php?dir=Articles/ ©Проф. Зайченко Ю.П.