Дискриминантный анализ является разделом многомерного статистического анализа, который позволяет изучать различия между двумя и более группами объектов по нескольким переменным одновременно. Дискриминантный анализ — это общий термин, относящийся к нескольким тесно связанным статистическим процедурам. Эти процедуры можно разделить на методы интерпретации межгрупповых различий — дискриминации и методы классификации наблюдений по группам. При интерпретации нужно ответить на вопрос: возможно ли, используя данный набор переменных, отличить одну группу от другой, насколько хорошо эти переменные помогают провести дискриминацию и какие из них наиболее информативны?.
Методы классификации связаны с получением одной или нескольких функций, обеспечивающих возможность отнесения данного объекта к одной из групп. Эти функции называются классифицирующими и зависят от значений переменных таким образом, что появляется возможность отнести каждый объект к одной из групп.
Задачи дискриминантного анализа можно разделить на три типа. Задачи первого типа часто встречаются в медицинской практике. Допустим, что мы располагаем информацией о некотором числе индивидуумов, болезнь каждого из которых относится к одному из двух или более диагнозов. На основе этой информации нужно найти функцию, позволяющую поставить в соответствие новым индивидуумам характерные для них диагнозы. Построение такой функции и составляет задачу дискриминации.
Второй тип задачи относится к ситуации, когда признаки принадлежности объекта к той или иной группе потеряны, и их нужно восстановить. Примером может служить определение пола давно умершего человека по его останкам, найденным при археологических раскопках.
Задачи третьего типа связаны с предсказанием будущих событий на основании имеющихся данных. Такие задачи возникают при прогнозе отдаленных результатов лечения, например, прогноз выживаемости оперированных больных.
2. ТЕОРЕТИЧЕСКАЯ ЧАСТЬОсновной целью дискриминации является нахождение такой линейной комбинации переменных (в дальнейшем эти переменные будем называть дискриминантными переменными), которая бы оптимально разделила рассматриваемые группы. Линейная функция
Коэффициенты![]() первой канонической дискриминантной функции выбираются таким образом, чтобы
центроиды различных групп как можно больше отличались друг от друга. Коэффициенты
второй группы выбираются также, но при этом налагается дополнительное условие,
чтобы значения второй функции были некоррелированы со значениями первой.
Аналогично определяются и другие функции. Отсюда следует, что любая каноническая
дискриминантная функция
первой канонической дискриминантной функции выбираются таким образом, чтобы
центроиды различных групп как можно больше отличались друг от друга. Коэффициенты
второй группы выбираются также, но при этом налагается дополнительное условие,
чтобы значения второй функции были некоррелированы со значениями первой.
Аналогично определяются и другие функции. Отсюда следует, что любая каноническая
дискриминантная функция ![]() имеет нулевую внутригрупповую корреляцию с
имеет нулевую внутригрупповую корреляцию с ![]() .
Если число групп равно g, то число канонических дискриминантных
функций будет на единицу меньше числа групп. Однако по многим причинам
практического характера полезно иметь одну, две или же три дискриминантных
функций. Тогда графическое изображениее объектов будет представлено в одно–,
двух– и трехмерных пространствах. Такое представление особенно полезно
в случае, когда число дискриминантных переменных p велико по сравнению
с числом групп g.
.
Если число групп равно g, то число канонических дискриминантных
функций будет на единицу меньше числа групп. Однако по многим причинам
практического характера полезно иметь одну, две или же три дискриминантных
функций. Тогда графическое изображениее объектов будет представлено в одно–,
двух– и трехмерных пространствах. Такое представление особенно полезно
в случае, когда число дискриминантных переменных p велико по сравнению
с числом групп g.
Для получения коэффициентов ![]() канонической дискриминантной функции нужен статистический критерий различения
групп. Очевидно, что классификация переменных будет осуществляться тем
лучше, чем меньше рассеяние точек относительно центроида внутри группы
и чем больше расстояние между центроидами групп. Разумеется,
что большая внутригрупповая вариация нежелательна, так как в этом случае
любое заданное расстояние между двумя средними тем менее значимо в статистическом
смысле, чем больше вариация распределений, соответствующих этим средним.
Один из методов поиска наилучшей дискриминации данных заключается в нахождении
такой канонической дискриминантной функции d, которая бы максимизировала
отношение межгрупповой вариации к внутригрупповой [1,2,3,4]
канонической дискриминантной функции нужен статистический критерий различения
групп. Очевидно, что классификация переменных будет осуществляться тем
лучше, чем меньше рассеяние точек относительно центроида внутри группы
и чем больше расстояние между центроидами групп. Разумеется,
что большая внутригрупповая вариация нежелательна, так как в этом случае
любое заданное расстояние между двумя средними тем менее значимо в статистическом
смысле, чем больше вариация распределений, соответствующих этим средним.
Один из методов поиска наилучшей дискриминации данных заключается в нахождении
такой канонической дискриминантной функции d, которая бы максимизировала
отношение межгрупповой вариации к внутригрупповой [1,2,3,4]
где B — межгрупповая и W внутригрупповая матрицы рассеяния наблюдаемых переменных от средних. В некоторых работах [3,4] в (2) вместо W используют матрицу рассеяния T объединенных данных.
Рассмотрим максимизацию отношения (2) для произвольного числа классов. Введем следующие обозначения:
![]() — число классов;
— число классов;
![]() число дискриминантных
переменных;
число дискриминантных
переменных;
![]() — число наблюдений
в k–й группе;
— число наблюдений
в k–й группе;
![]() — общее число
наблюдений по всем группам;
— общее число
наблюдений по всем группам;
![]() — величина переменной i
для m–го наблюдения в k–й группе;
— величина переменной i
для m–го наблюдения в k–й группе;
![]() — средняя величина
переменной i в k–й группе;
— средняя величина
переменной i в k–й группе;
![]() — среднее значение
переменной i по всем группам;
— среднее значение
переменной i по всем группам;
![]() — общая сумма перекрестных
произведений для переменных u и v;
— общая сумма перекрестных
произведений для переменных u и v;
![]() — внутригрупповая
сумма перекрестных произведений для переменных u и v.
— внутригрупповая
сумма перекрестных произведений для переменных u и v.
![]() ;
; ![]() .
.
В модели дискриминации должны соблюдаться следующие условия:
Рассмотрим задачу максимизации отношения (2) когда имеются
g групп. Оценим сначала информацию, характеризующую степень различия между
объектами по всему пространству точек, определяемому переменными групп.
Для этого вычислим матрицу рассеяния T, которая равна сумме
квадратов отклонений и попарных произведений наблюдений от общих средних ![]() по каждой переменной. Элементы матрицы T определяются выражением [3,4]
по каждой переменной. Элементы матрицы T определяются выражением [3,4]
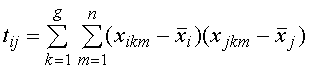 , (3)
, (3)
где 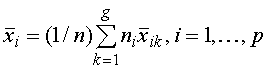 ;
;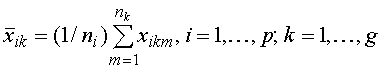 .
.
Запишем это выражение в матричной форме. Обозначим p–мерную случайную векторную переменную k-ой группы следующим образом
![]() .
.
Тогда объединенная p-мерная случайная векторная переменная всех групп будет иметь вид
![]()
Общее среднее этой p-мерной случайной векторной переменной будет равен вектору средних отдельных признаков
![]() .
.
Матрица рассеяния от среднего при этом запишется в виде
![]() . (4)
. (4)
Если использовать векторную переменную объединенных переменных X,
то матрица Матрица T содержит полную информацию о распределении
точек по пространству переменных. Диагональные элементы представляют собой
сумму квадратов отклонений от общего среднего и показывают как ведут себя
наблюдения по отдельно взятой переменной. Внедиагональные элементы равны
сумме произведений отклонений по одной переменной на отклонения по другой. Если разделить матрицу T на Для измерения степени разброса объектов внутри групп рассмотрим
матрицу W, которая отличается от T только тем, что
ее элементы определяются векторами средних для отдельных групп, а не вектором
средних для общих данных. Элементы внутригруппового рассеяния определятся
выражением
Запишем это выражение в матричной форме. Данным g групп будут соответствовать векторы средних Тогда матрица внутригрупповых вариаций запишется в виде Если разделить каждый элемент матрицы W на (n–g), то получим оценку ковариационной матрицы внутригрупповых данных. Когда центроиды различных групп совпадают, то элементы матриц T и
W будут равны. Если же центроиды групп различные, то разница
Матрицы W и B содержат всю основную
информацию о зависимости внутри групп и между группами. Для лучшего разделения
наблюдений на группы нужно подобрать коэффициенты дискриминантной функции
из условия максимизации отношения межгрупповой матрицы рассеяния к внутригрупповой
матрице рассеяния при условии ортогональности дискриминантных плоскостей.
Тогда нахождение коэффициентов дискриминантных функций сводится к решению
задачи о собственных значениях и векторах [3]. Это утверждение можно сформулировать
так: если спроектировать Пусть что влечет равенство где Каждое решение, которое имеет свое собственное значение Нормированные коэффициенты (11) получены по нестандартизованным исходным данным, поэтому они называются
нестандартизованными. Нормированные коэффициенты приводят к таким дискриминантным значениям, единицей измерения
которых является стандартное квадратичное отклонение. При таком подходе каждая ось в преобразованном пространстве сжимается или растягивается таким образом, что соответствующее дискриминантное значение для данного объекта представляет собой число стандартных отклонений точки от главного центроида. Стандартизованные коэффициенты можно получить двумя способами: где Стандартизованные коэффициенты полезно применять для уменьшения размерности исходного признакового пространства
переменных. Если абсолютная величина коэффициента для данной переменной для всех дискриминантных функций мала, то эту переменную можно исключить, тем самым сократив число переменных. Структурные коэффициенты определяются коэффициентами взаимной корреляции между отдельными переменными и дискриминантной функцией. Если относительно некоторой переменной абсолютная величина коэффициента
велика, то вся информация о дискриминантной функции заключена в этой переменной. Структурные коэффициенты полезны при классификации групп. Структурный коэффициент можно вычислить и для переменной в пределах отдельно взятой группы. Тогда получаем внутригрупповой структурный коэффициент,
который где Структурные коэффициенты по своей информативности несколько отличаются от стандартизованных коэффициентов. Стандартизованные коэффициенты показывают вклад переменных в значение дискриминантной функции. Если две переменные сильно коррелированы, то их стандартизованные коэффициенты могут быть меньше по сравнению с теми случаями, когда используется только одна из этих переменных. Такое распределение величины стандартизованного коэффициента объясняется тем, что при их вычислении учитывается влияние всех переменных.Структурные же коэффициенты являются парными корреляциями и на них не влияют взаимные зависимости прочих переменных. Общее число дискриминантных функций не превышает числа дискриминантных переменных и, по крайней мере, на 1 меньше числа групп. Степень разделения выборочных групп зависит от величины собственных чисел: чем больше собственное число, тем сильнее разделение. Наибольшей разделительной способностью обладает первая дискриминантная функция, соответствующая наибольшему
собственному числу Коэффициент канонической корреляции. Другой характеристикой, позволяющей оценить полезность дискриминантной функции является коэффициент канонической корреляции Чем больше величина Остаточная дискриминация.Так как дискриминантные функции находятся по выборочным данным, они нуждаются в проверке статистической значимости. Дискриминантные функции представляются аналогично главным компонентам. Поэтому для проверки этой значимости можно воспользоваться критерием, аналогичным дисперсионному критерию в методе
главных компонент. Этот критерий оценивает остаточную дискриминантную способность, под которой понимается способность различать группы, если при этом исключить информацию, полученную с помощью ранее вычисленных функций. Если остаточная
дискриминация мала, то не имеет смысла дальнейшее вычисление очередной дискриминантной функции. Полученная статистика носит название " где k — число вычисленных функций. Чем меньше эта статистика, тем значимее соответствующая дискриминантная функция. Величина имеет хи–квадрат распределение с Вычисления проводим в следующем порядке: До сих пор мы рассматривали получение канонических дискриминантных функций при известной принадлежности объектов к тому или иному классу. Основное внимание уделялось определению числа и значимости этих функций, и использованию их для объяснения различий между классами. Все сказанное относилось к интерпретации результатов ДА. Однако наибольший интерес представляет задача предсказания класса, которому принадлежит некоторый случайно выбранный объект. Эту задачу можно решить, используя информацию, содержащуюся в дискриминантных переменных. Существуют различные способы классификации. В процедурах классификации могут использоваться как сами дискриминантные переменные, так и канонические дискриминантные функции. В первом случае применяется метод максимизации различий между классами для получения функции классификации, различие же классов на значимость не проверяется и, следовательно, дискриминантный анализ не проводится. Во втором случае для классификации используются непосредственно дискриминантные функции и проводится более глубокий анализ. Рассмотрим случай отнесения случайно выбранного объекта Определим условную вероятность Из теоремы Байеса получаем Выражение (17) справедливо для любого распределения вектора х. Байесовская процедура минимизирует ожидаемую вероятность ошибочной классификации Так, например, для двух групп получим: Эта величина является вероятностью того, что объект, принадлежащий к группе Если х имеет p–мерный нормальный закон распределения Байесовская процедура классификации состоит в том, что вектор наблюдений х относится к группе Можно показать, что байесовская процедура эквивалентна отнесению вектора х к группе является максимальной. Подставим в оценочную функцию (19) формулу нормального закона распределения Удаляя общую константу Преобразуем выражение (20) >и, удалив постоянную Заменим векторы средних и ковариационную матрицу их оценками Введем обозначения где Объект где Функции, определяемые соотношением (22), называются "простыми классифицирующими функциями" потому, что они предполагают лишь равенство групповых ковариационных матриц и не требуют других дополнительных свойств. Выбор функций расстояния между объектами для классификации является наиболее очевидным способом введения меры сходства для векторов объектов, которые интерпретируются как точки в евклидовом пространстве. В качестве меры сходства можно использовать евклидово расстояние между объектами. Чем меньше расстояние между объектами, тем больше сходство. Однако в тех случаях, когда переменные коррелированы, измерены в разных единицах и имеют различные стандартные отклонения, трудно четко определить
понятие "расстояния". В этом случае полезнее применить не евклидовое расстояние, а выборочное расстояние Махаланобиса или в матричной записи где х представляет объект с р переменными, При использовании функции расстояния, объект относят к той группе, для которой расстояние Относя объект к ближайшему классу в соответствии с Объект принадлежит к той группе, для которой апостериорная вероятность До сих пор при классификации по Это изменение расстояния математически идентично умножению величин Отметим, тот факт, что априорные вероятности оказывают наибольшее влияние при перекрытии групп и, следовательно, многие объекты с большой вероятностью могут принадлежать ко многим группам. Если группы сильно различаются, то учет априорных вероятностей практически не влияет на результат классификации, поскольку между классами будет находиться очень мало объектов. V–статистика Рао. В некоторых работах для классификации используется обобщенное расстояние Махаланобиса V — обобщение величины Матричное выражение оценки V имеет вид Отметим, что при включении или исключении переменных V–статистика имеет распределение хи–квадрат с числом степеней свободы, равным В дискриминантном анализе процедура классификации используется для определения принадлежности к той или иной группе случайно выбранных объектов, которые не были включены при выводе дискриминантной и классифицирующих функций. Для проверки точности классификации применим классифицирующие функции к тем объектам, по которым они были получены. По доле правильно
классифицированных объектов можно оценить точность процедуры классификации. Результаты такой классификации представляют в виде классификационной матрицы. Рассмотрим пример классификационной матрицы, приведенной в таблице 1.
В первой группе точно предсказаны из 10 объектов 9, что составляет 90%, один объект отнесен к 4–й группе. Во второй группе правильно предсказаны 80% объектов, один объект (20%) отнесен к третьей группе. В третьей группе процент правильного предсказания самый низкий и составляет 68,5%, причем из 54 объектов 8 отнесены к первой группе, 4 — ко второй и 5 — к четвертой группе. В четвертой группе правильно предсказаны 84,6%, по одному объекту отнесено к первой и третьей группам. Процент правильной классификации объектов является дополнительной мерой различий между группами и ее можно считать наиболее подходящей мерой дискриминации. Следует отметить, что величина процентного содержания пригодна для суждения о правильном предсказании только тогда, когда распределение объектов по группам производилось случайно. Например, для двух групп при случайной классификации можно правильно предсказать 50%, а для четырех групп эта величина составляет 25%. Поэтому если для двух групп имеем 60% правильного предсказания, то нужно считать эту величину слишком малой, тогда как для четырех групп эта величина говорит о хорошей разделительной способности. Пример. Больные гипертиреозом (увеличение щитовидной железы) общим числом 23 человека были разделены на три группы: По результатам обследования 23 пациентов имеются следующие измерения: Конкретные результаты приведены в таблице 2. По матрице исходных данных находятся средниеи стандартные отклонения дискриминантных переменных (таблицы 3 и 4), общая T и внутригрупповые W матрицы сумм квадратов и перекрестных произведений). Если разделить каждый элемент T на ( Из общей корреляционной матрицы видно, что переменные некоррелированы на уровне 0.01. Отсюда следует, что ни одна переменная не может быть предсказана по значению, соответствующему другой переменной. Для измерения меры разброса наблюдений внутри классов используется внутригрупповая корреляционная матрица, которая приведена в таблице 8. Эта матрица не совпадает с общей корреляционной матрицей. Из таблицы видно, что многие коэффициенты отличаются от значений, приведенных в таблице 7. Отмечается значимая корреляция переменной IGM со всеми остальными переменными на уровне 0,05. Из таблиц 5 и 6 видно, что большая часть элементов матрицы W меньше соответствующих элементов матрицы T. Разница этих матриц Для нахождения коэффициентов канонической дискриминантной функции решаем задачу (2) в терминах собственных чисел и векторов, которая в матричной записи имеет вид (10). Систему уравнений (10) решаем с помощью разложения Холецкого матрицы Наибольшее собственное значение для системы равно При использовании коэффициентов b начало координат не будет совпадать
с главным центроидом. Для того, чтобы начало координат совпало с главным центроидом нужно нормировать компоненты вектора b, используя формулы (11). Для оценки относительного вклада каждой переменной в значение дискриминантной
функции вычислим стандартизованные дискриминантные коэффициенты по формуле (12). Результаты вычислений приведены в таблице 10 и таблице 11. Из таблице 11 видно, что две наиболее значимо коррелированные переменные Y6 и Y9 имеют примерно одинаковые стандартизованные коэффициенты. Значения нестандартизованной
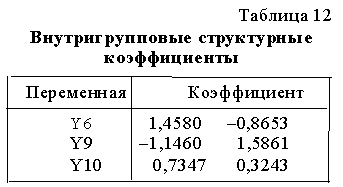
канонической функции для каждого пациента сведены в таблице 16. Координаты центроидов первой, второй и третьей групп соответственно равны: Для определения взаимной зависимости отдельной переменной и дискриминантной функции рассмотрим внутригрупповые структурные коэффициенты, значения которых находим по формуле (13). Результаты вычислений представлены в таблице 12. Переменные Y6 и Y9 имеют небольшие структурные коэффициенты, но у них относительно большие стандартизованные коэффицинты. Это объясняется значимой корреляцией переменной Y6 с другими переменными и может оказаться, что вклад переменных Y6 и Y9 в дискриминантые значения невелик. Для оценки реальной полезности канонической дискриминантной функции вычисляем по формулам
(14) — (16) коэффициент канонической корреляции, Λ–статистику Уилкса, статистику хи–квадрат, уровень значимости. Результаты вычислений приведены в таблице 13.
Данные таблицы указывают на хорошую дискриминацию групп: большая величина канонической корреляции соответствует тесной связи дискриминантной функции с группами; малая величина Λ–статистики Уилкса означает, что четыре используемых переменных эффективно участвуют в различении групп и, наконец, статистика χ–квадрат значима с уровнем 1,6⋅10-8. Процедура классификации. Процедуры классификации могут использовать канонические дискриминантные функции или сами дискриминантные переменные. Для классификации с помощью дискриминантных переменных коэффициенты классифицирующей функции вычисляем по формуле (22). Результаты вычислений приведены в таблице 14. Значения классифицирующей функции для каждого больного вычислены по формуле (21), результаты классификации в виде классификационной матрицы представлены в таблице 15. Так как процент правильной классификации составляет 100%, то таблицу классифицирующих функций для отдельных пациентов можно не представлять. Результаты классификации с помощью расстояния Махаланобиса (формулы (25), (26)) и апостериорной вероятности принадлежности к группе в предположении нормальности распределения (формула 19) приведены в таблице 15. Каримов Р.Н. Основы дискриминантного анализа. Учебно–методическое пособие. — Саратов: СГТУ, 2002. — 108 с.: ил.![]()
![]() ,
то получим ковариационную матрицу. Для проверки условия линейной независимости
переменных полезно рассмотреть вместо T нормированную корреляционную
матрицу.
,
то получим ковариационную матрицу. Для проверки условия линейной независимости
переменных полезно рассмотреть вместо T нормированную корреляционную
матрицу.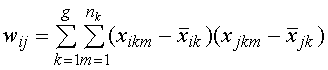 . (5)
. (5)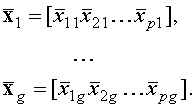 (6)
(6)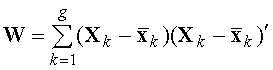 . (7)
. (7)![]() (8)
(8)
будет определять межгрупповую сумму квадратов отклонений
и попарных произведений. Если расположение групп в пространстве различается
(т.е. их центроиды не совпадают), то степень разброса наблюдений внутри
групп будет меньше межгруппового разброса. Отметим, что элементы матрицы
В
можно вычислить и по данным средних.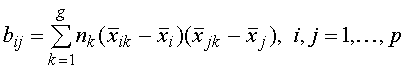 (9)
(9)![]() групп р–мерных выборок на
групп р–мерных выборок на ![]() пространство, порожденное собственными векторами
пространство, порожденное собственными векторами ![]() ,
то отношение (2) будет максимальным, т.е. рассеивание между группами будет
максимальным при заданном внутригрупповом рассеивании. Если бы мы захотели
спроектировать g выборок на прямую при условии максимизации наибольшего
рассеивания между группами, то следовало бы использовать собственный вектор
,
то отношение (2) будет максимальным, т.е. рассеивание между группами будет
максимальным при заданном внутригрупповом рассеивании. Если бы мы захотели
спроектировать g выборок на прямую при условии максимизации наибольшего
рассеивания между группами, то следовало бы использовать собственный вектор ![]() ),
соответствующий максимальному собственному числу
),
соответствующий максимальному собственному числу ![]() .
При этом дискриминантные функции можно получать: по нестандартизованным
и стандартизованным коэффициентам.
.
При этом дискриминантные функции можно получать: по нестандартизованным
и стандартизованным коэффициентам.![]() и
и ![]() соответственно собственные
значения и векторы. Тогда условие (2) в терминах собственных чисел и векторов
запишется в виде
соответственно собственные
значения и векторы. Тогда условие (2) в терминах собственных чисел и векторов
запишется в виде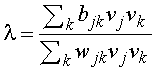 ,
,![]() ,
или в матричной записи
,
или в матричной записи![]() , (10)
, (10)![]() — символ
Кронекера. Таким образом, решение уравнения
— символ
Кронекера. Таким образом, решение уравнения ![]() позволяет нам определить компоненты собственных векторов, соответствующих дискриминантным функциям. Если B и
W невырожденные матрицы, то собственные корни уравнения
позволяет нам определить компоненты собственных векторов, соответствующих дискриминантным функциям. Если B и
W невырожденные матрицы, то собственные корни уравнения ![]() такие же, как и у
такие же, как и у ![]() . Решение
системы уравнений (10) можно получить путем использования разложения Холецкого
. Решение
системы уравнений (10) можно получить путем использования разложения Холецкого ![]() матрицы
матрицы ![]() и решения задачи
о собственных значениях
и решения задачи
о собственных значениях![]() .
.![]() и собственный вектор
и собственный вектор ![]() ,
соответствует одной дискриминантной функции. Компоненты собственного вектора
,
соответствует одной дискриминантной функции. Компоненты собственного вектора ![]() можно использовать в качестве коэффициентов дискриминантной функции. Однако при таком подходе начало координат не будет совпадать с главным центроидом. Для того, чтобы начало координат совпало с главным центроидом нужно нормировать
компоненты собственного вектора [4]
можно использовать в качестве коэффициентов дискриминантной функции. Однако при таком подходе начало координат не будет совпадать с главным центроидом. Для того, чтобы начало координат совпало с главным центроидом нужно нормировать
компоненты собственного вектора [4]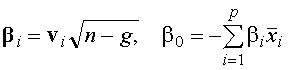 . (11)
. (11)
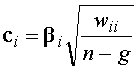 , (12)
, (12)![]() сумма внутригрупповых квадратов
сумма внутригрупповых квадратов
![]() й переменной, определяемой по формуле (5).
й переменной, определяемой по формуле (5).![]() вычисляется по формуле:
вычисляется по формуле: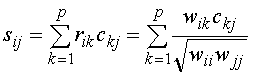 , (13)
, (13)![]() внутригрупповой
структурный коэффициент для i–ой переменной и j–ой функции;
внутригрупповой
структурный коэффициент для i–ой переменной и j–ой функции; ![]() — внутригрупповые структурные коэффициенты корреляции между переменными i и k;
— внутригрупповые структурные коэффициенты корреляции между переменными i и k; ![]() — стандартизованные коэффициенты канонической функции для переменной k и функции j.
— стандартизованные коэффициенты канонической функции для переменной k и функции j.
Число дискриминантных функций
![]() , вторая обеспечивает максимальное различение после первой и т.д. Различительную способность i–ой функции оценивают по относительной величине
в процентах собственного числа
, вторая обеспечивает максимальное различение после первой и т.д. Различительную способность i–ой функции оценивают по относительной величине
в процентах собственного числа ![]() от суммы всех
от суммы всех ![]() .
.![]() . Каноническая корреляция является мерой связи между двумя множествами переменных. Максимальная величина этого коэффициента равна 1. Будем считать, что группы составляют одно множество, а другое множество образуют дискриминантные
переменные. Коэффициент канонической корреляции для i–ой дискриминантной функции определяется формулой:
. Каноническая корреляция является мерой связи между двумя множествами переменных. Максимальная величина этого коэффициента равна 1. Будем считать, что группы составляют одно множество, а другое множество образуют дискриминантные
переменные. Коэффициент канонической корреляции для i–ой дискриминантной функции определяется формулой: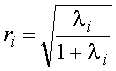 . (14)
. (14)![]() , тем лучше разделительная способность дискриминантной функции.
, тем лучше разделительная способность дискриминантной функции.![]() " и вычисляется по формуле:
" и вычисляется по формуле:![]() , (15)
, (15)![]() (16)
(16)![]() степенями свободы.
степенями свободы.
![]() при k=0. Значимость критерия подтверждает существование различий между группами. Кроме того, это доказывает, что первая дискриминантная
функция значима и имеет смысл ее вычислять.
при k=0. Значимость критерия подтверждает существование различий между группами. Кроме того, это доказывает, что первая дискриминантная
функция значима и имеет смысл ее вычислять.Классифицирующие функции
![]() к одной из групп
к одной из групп ![]() . Пусть
. Пусть ![]() плотность распределения х в
плотность распределения х в ![]() и
и ![]() априорная вероятность того, что вектор х принадлежит к группе
априорная вероятность того, что вектор х принадлежит к группе ![]() . Предполагается, что сумма априорных вероятностей
. Предполагается, что сумма априорных вероятностей ![]() равна 1.
равна 1.![]() получения некоторого вектора х, если известно, что объект принадлежит к группе
получения некоторого вектора х, если известно, что объект принадлежит к группе ![]() . Обозначим через
. Обозначим через ![]() условную вероятность принадлежности объекта к группе
условную вероятность принадлежности объекта к группе ![]() при заданном х. Величины
при заданном х. Величины ![]() и
и ![]() называются апостериорными вероятностями. Различие между априорными и апостериорными вероятностями заключается в следующем. Априорная вероятность
называются апостериорными вероятностями. Различие между априорными и апостериорными вероятностями заключается в следующем. Априорная вероятность ![]() равна вероятности принадлежности объекта к данной группе
равна вероятности принадлежности объекта к данной группе ![]() до получения вектора наблюдений х. Апостериорная вероятность
до получения вектора наблюдений х. Апостериорная вероятность ![]() определяет вероятность принадлежности объекта к группе
определяет вероятность принадлежности объекта к группе ![]() только после анализа вектора наблюдений х этого объекта.
только после анализа вектора наблюдений х этого объекта.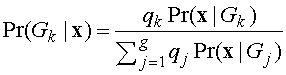 . (17)
. (17)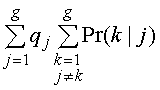 .
.![]() .
.![]() , ошибочно классифицируется, как принадлежащий
, ошибочно классифицируется, как принадлежащий ![]() , или, наоборот, объект из
, или, наоборот, объект из ![]() ошибочно относится к
ошибочно относится к ![]() .
.![]() , то вероятности
, то вероятности ![]() можно заменить соответственно на плотности распределений
можно заменить соответственно на плотности распределений ![]() .
В результате получим:
.
В результате получим: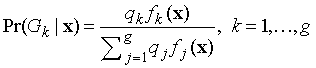 . (18)
. (18)![]() , если
, если ![]() имеет наибольшее значение.
имеет наибольшее значение.![]() , если оценочная функция
, если оценочная функция![]() (19)
(19)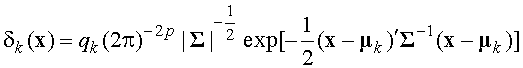 .
.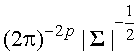 и логарифмируя, получим:
и логарифмируя, получим: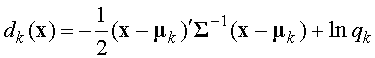 . (20)
. (20)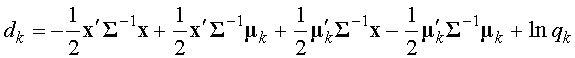
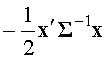 , получим
, получим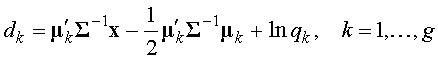 .
.![]() и
и ![]() . Тогда получим классифицирующую функцию.
. Тогда получим классифицирующую функцию.![]() и
и 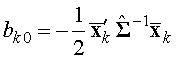 ,
, ![]() ,
,![]() и
и![]() — коэффициенты k–ой классифицирующей функции i–го объекта (простой дискриминантной функции Фишера)
— коэффициенты k–ой классифицирующей функции i–го объекта (простой дискриминантной функции Фишера)![]() . (22)
. (22)![]() относится к классу, у которого значение
относится к классу, у которого значение ![]() оказывается наибольшим. Коэффициенты классифицирующих функций удобнее вычислять по скалярным выражениям
оказывается наибольшим. Коэффициенты классифицирующих функций удобнее вычислять по скалярным выражениям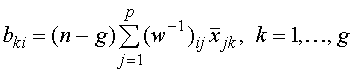 , (23)
, (23)![]() коэффициент для переменной i в выражении, соответствующему классу k,
коэффициент для переменной i в выражении, соответствующему классу k, ![]() обратный элемент внутригрупповой матрицы сумм попарных произведений W. Постоянный член находится по формуле
обратный элемент внутригрупповой матрицы сумм попарных произведений W. Постоянный член находится по формуле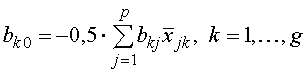 . (24)
. (24)
![]() (25)
(25)![]() , (25')
, (25')![]() –вектор средних для переменных k–ой группы объектов. Если вместо
–вектор средних для переменных k–ой группы объектов. Если вместо ![]() использовать оценку внутригрупповой ковариационной матрицы
использовать оценку внутригрупповой ковариационной матрицы ![]()
![]() ,
то получим стандартную запись выборочного расстояния Маханалобиса
,
то получим стандартную запись выборочного расстояния Маханалобиса![]() . (26)
. (26)![]() наименьшее.
наименьшее.![]() , мы неявно приписываем его к тому классу, для которого он имеет наибольшую вероятность принадлежности
, мы неявно приписываем его к тому классу, для которого он имеет наибольшую вероятность принадлежности ![]() . Если предположить, что любой объект должен принадлежать одной из групп,
то можно вычислить вероятность его принадлежности для любой из групп
. Если предположить, что любой объект должен принадлежать одной из групп,
то можно вычислить вероятность его принадлежности для любой из групп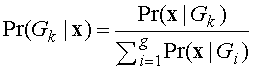 . (27)
. (27)![]() максимальна, что эквивалентно использованию наименьшего расстояния.
максимальна, что эквивалентно использованию наименьшего расстояния.![]() предполагалось, что априорные вероятности появления групп одинаковы. Для учета априорных вероятностей нужно модифицировать расстояние
предполагалось, что априорные вероятности появления групп одинаковы. Для учета априорных вероятностей нужно модифицировать расстояние ![]() , вычитая из выражений (32) — (34) удвоенную величину натурального логарифма от априорной вероятности
, вычитая из выражений (32) — (34) удвоенную величину натурального логарифма от априорной вероятности ![]() . Тогда, вместо выборочного расстояния Махаланобиса (34), получим
. Тогда, вместо выборочного расстояния Махаланобиса (34), получим![]()
![]() . (28)
. (28)![]() на априорную вероятность группы
на априорную вероятность группы ![]() . Формулу (28) можно получить, умножив правые и левые части выражения (20) на два. Тогда после замены векторов средних и ковариационной матрицы их
оценками имеем
. Формулу (28) можно получить, умножив правые и левые части выражения (20) на два. Тогда после замены векторов средних и ковариационной матрицы их
оценками имеем![]() .
.![]() . Эта мера, известная как V–статистика Рао, измеряет расстояния от каждого центроида группы до главного центроида с весами, пропорциональными объему выборки соответствующей группы. Она применима при любом количестве классов
и может быть использована для проверки гипотезы
. Эта мера, известная как V–статистика Рао, измеряет расстояния от каждого центроида группы до главного центроида с весами, пропорциональными объему выборки соответствующей группы. Она применима при любом количестве классов
и может быть использована для проверки гипотезы ![]() . Если гипотеза
. Если гипотеза ![]() верна, а объемы выборок
верна, а объемы выборок ![]() стремятся к
стремятся к ![]() , то распределение величины V стремится к
, то распределение величины V стремится к ![]() с
с ![]() степенями свободы. Если наблюдаемая величина
степенями свободы. Если наблюдаемая величина ![]() , то гипотеза
, то гипотеза ![]() отвергается. V–статистика вычисляется по формуле
отвергается. V–статистика вычисляется по формуле![]() . (29)
. (29)![]() . (30)
. (30)![]() , умноженное на число переменных, включенных (исключенных) на этом шаге. Если изменение статистики не значимо, то переменную можно не включать. Если после включения новой переменной V–статистика оказывается отрицательной, то это означает, что включенная переменная ухудшает разделение центроидов.
, умноженное на число переменных, включенных (исключенных) на этом шаге. Если изменение статистики не значимо, то переменную можно не включать. Если после включения новой переменной V–статистика оказывается отрицательной, то это означает, что включенная переменная ухудшает разделение центроидов.
Группы Предсказанные группы(число/процент)
1
2
3
4
Всего
1
9
90.0
0
0.0
0
0.0
1
0.0
10
2
0
0.0
4
80.0
1
20.0
0
0.0
5
3
8
14.8
4
7.4
37
68.5
5
9.3
54
4
1
7.7
0
0.0
1
7.7
11
84.6
13
N Гр. y6 y9 y10
1 1 14.4 25.1 0.20 2 1 20.1 40.1 0.11 3 1 24.1 32.1 0.17 4 1 11.1 16.9 0.12 5 1 16.3 32.1 0.36 6 1 40.5 64.4 0.21 7 1 52.7 50.0 0.53 8 1 20.8 22.3 0.13 9 1 14.0 3.1 0.18 10 1 27.0 41.7 0.19 11 1 44.3 63.8 0.22 12 1 47.5 50.1 0.29 13 1 54.0 57.0 0.19 14 1 16.1 20.6 0.22 15 1 57.5 74.5 0.49 16 1 37.8 63.0 0.32 17 2 55.8 48.0 2.74 18 2 75.0 60.0 1.37 19 2 72.0 65.0 0.70 20 2 70.6 45.0 1.40 21 3 24.1 45.0 0.22 22 3 33.2 55.0 0.01 23 3 30.4 44.6 0.09
![]()
Группы
Y6
Y9
Y10
Кол–во
1 (
![]() )
)31,1375
41,0500
0,2456
16
2 (
![]() )
)68,3500
54,5000
1,5525
4
3 (
![]() )
)29,2333
48,2000
0,1067
3
Все группы (
![]() )
)37,3609
44,3217
0,4548
23
![]()
Группы
Y6
Y9
Y10
Кол–во
1.
![]()
16,2739
20,4760
0,1237
16
2.
![]()
8,5656
9,5394
0,8551
4
3.
![]()
4,б608
5,8924
0,1060
3
Все группы
![]()
23
Переменная
Y6
Y9
Y10
Y6
8895,3148
6025,1896
163,2293
Y9
6025,1896
7262,2391
53,5466
Y10
163,2293
53,5466
8,3290
Переменная
Y6
Y9
Y10
Y6
4236,1542
4532,3100
–2,1545
Y9
4532,3100
6631,4600
1,9565
Y10
–2,1545
1,9565
2,4455
![]() ),
а каждый элемент W — на (
),
а каждый элемент W — на (![]() ),
то получим ковариационные матрицы. Для оценки меры связи между дискриминантными переменными матрицы T и W преобразованы в корреляционные матрицы, которые приведены в таблицах 7 и 8. Элементы этих матриц найдены по формулам
),
то получим ковариационные матрицы. Для оценки меры связи между дискриминантными переменными матрицы T и W преобразованы в корреляционные матрицы, которые приведены в таблицах 7 и 8. Элементы этих матриц найдены по формулам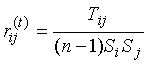 и
и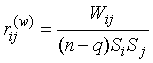 .
.
Переменная
Y6
Y9
Y10
Y6
1,0000
-0,1759
0,0664
Y9
-0,1759
1,0000
0,3480
Y10
0,0664
0,3480
1,0000
Переменная
Y6
Y9
Y10
Y6
1,0000
0,8551
–0,0212
Y9
0,8551
1,0000
0,0154
Y10
–0,0212
0,0154
1,00
![]() определяет межгрупповую сумму квадратов отклонений и попарных произведений. Эта матрица приведена в таблице 9.
определяет межгрупповую сумму квадратов отклонений и попарных произведений. Эта матрица приведена в таблице 9.
Переменная
Y6
Y9
Y10
Y6
4659,1606
1492,8796
165,3838
Y9
1492,8796
630,7791
51,5901
Y10
165,3838
51,5901
5,8834
![]() =
= ![]() ,
, ![]() .
.![]() и
и ![]() , которым соответствуют собственные векторы
, которым соответствуют собственные векторы ![]() и
и ![]() .
Положив
.
Положив ![]() , получаем коэффициенты
канонической дискриминантной функции
, получаем коэффициенты
канонической дискриминантной функции ![]() и
и ![]() .
.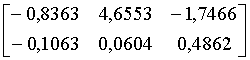 .
.
Переменная
Коэффициенты
Y6
0,0978
-0,0580
Y9
-0,0614
0,0850
Y10
2,0504
0,9050
Константа
-1,8628
-0,20112
Переменная
Коэффициенты
Y6
1,4228
-0,8445
Y9
-1,1184
1,5479
Y10
0,7170
0,33165
Собств. знач.
5,3514
0,0452
Дискр. функция
Собственное значение
Каноническая корреляция R
Λ–cтатистика Уилкса
Статистика χ–квадрат
Степ. свободы
Уровень значимости.
1
5,3514
0,9179
0,1506
35,9655
6
4,076⋅10-6
2
0,0452
0,2080
0,9567
0,8405
2
0,6569
Переменная
Группа 1
Группа 2
Группа 3
Y6
0,0603
0,5875
–0,0631
Y9
0,0820
–2,4110
0,1883
Y10
1,9962
13,4071
0,6661
Константа
–2,8760
–23,9141
–3,6512
Группы Предсказанные группы(число/процент)
1
2
3
Всего
1
10
62.50
0
0.0
6
37.50
16
2
0
0.0
4
100.0
0
0.0
4
3
0
0.0
0
0.0
3
100.0
3
N больного
Нестандартизованные канонические функции di
Квадрат расстояния Махаланобиса D2(x/Gk)
Группа
Значение
Группа 1
Группа 2
Группа 3
1
1
–1,6258
–0,5453
1,3941
39,9613
1,7126
2
1
–2,1879
0,3389
2,1281
46,4330
0,4254
3
1
–1,1576
–0,5402
0,3037
33,8515
1,4480
4
1
–1,6083
–1,1376
2,1155
40,6888
3,1499
5
1
–1,5398
0,0998
1,6444
39,0807
1,3698
6
1
–1,4635
1,3352
2,4410
38,6575
0,8729
7
1
–1,3373
–0,3477
5,3223
12,0657
10,6765
8
1
–1,2347
–0,9555
1,2544
32,8613
3,5611
9
1
–2,4564
–0,3223
5,7100
30,9378
10,5528
10
1
0,1421
–1,4293
0,4101
36,6478
0,2827
11
1
1,0663
–1,0241
1,6739
33,2676
1,1976
12
1
–0,2524
0,3058
0,1102
19,8784
5,5216
13
1
–0,1306
0,3126
3,2852
20,941
6,5678
14
1
–1,0198
–1,1302
1,2853
34,6955
3,0330
15
1
1,4639
0,1921
4,0840
22,5124
5,3097
16
1
1,4759
–1,4148
2,6895
38,3378
1,0454
17
2
1,3432
6,4170
60,6784
12,4824
73,1019
18
2
–0,0236
4,7068
29,9684
0,4904
40,9341
19
2
–0,0311
2,6839
14,5114
6,785
21,8918
20
2
–1,0408
5,2731
36,9560
1,7390
50,1042
21
3
0,6296
–1,8645
1,7390
42,4824
0,2744
22
3
0,7651
–2,0234
2,1344
44,5377
0,2310
23
3
0,0998
–1,4813
0,4413
37,2501
0,2704
3. ЛИТЕРАТУРА
Рецензент В.А. Борщев
Редактор Л.А. Мишина
Лицензия ЛР № 020271 от 15.11.96г.
Подписано в печать Формат 60 84 1/16
Бум. оберт. Усл.–печ.л. Уч. – изд.л.
Тираж 100 экз. Заказ Бесплатно
Саратовский государственный технический университет
410054 г, Саратов, ул. Политехническая, 77
Копипринт СГТУ, 410054, г. Саратов , ул. Политехническая,77