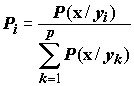 (8.19)
(8.19)Пусть задано пространство признаков X размерностью m>1, точками которого являются конкретные гидробиологические измерения x={x1,…, xi,…,xm}, где xi — значения численности или биомассы i–й таксономической группы гидробионтов в пробе, либо некоторые обобщенные индексы. Исходная таблица наблюдений разбита на P непересекающихся подмножеств строк, где каждой строке x поставлен в соответствие некоторый класс качества yk, k=1,2,…,p, причем любому из P классов принадлежит не менее одного объекта. Содержательный смысл задаваемой системы классификации {у1, у2,…, yp } применительно к гидробиологическим исследованиям может иметь вполне произвольное толкование (например, любые градации сапробности, токсобности, классов качества вод, типов водоемов, природно–климатических зон и т.д.).
Необходимо определить набор формальных решающих правил, позволяющих для произвольного измерения х из Х указать класс качества yk, к которому оно принадлежит.
Решающие правила, формируемые на основе вероятностных методов, могут быть получены:
Рекомендуемая литература: [Урбах, 1964; Дуда, Харт, 1978; Кравцов, Милютин, 1981; Айвазян с соавт., 1989; Ким с соавт., 1989].
Байесовская схема принятия решений
Параметрические методы распознавания для поиска оптимальных дискриминационных функций используют аппроксимацию функции вероятностного распределения исходных данных и сводятся к определению отношения правдоподобия в различных областях многомерного пространства признаков. Классификатор может быть непосредственно построен из формулы условных вероятностей Байеса, апеллирующей к априорным вероятностям принадлежности объектов к тому или иному распознаваемому классу и условным плотностям распределения значений вектора признаков.
Если априорные вероятности появления каждого класса равны, то вероятность того, что вектор x принадлежит классу yi равна:
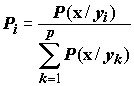 (8.19)
(8.19)Очевидно, что наибольшая из величин P(x/yi) и будет обеспечивать наименьшую вероятность неправильной классификации или наименьший средний риск. Решающее правило можно сформулировать следующим образом: вектор измерений х принадлежит классу yi, если
Предположим, например, что каждый класс измерений описывается нормальным распределением и ковариационные матрицы С всех классов одинаковы. Тогда дискриминантная функция имеет следующий вид [Стьюпер с соавт., 1982]:
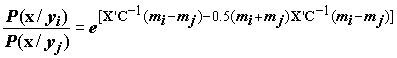 , (8.21)
, (8.21)где mi, mj — математические ожидания векторов классов i и j. Для того, чтобы классифицировать произвольный вектор х, нужно рассчитать значения функции для всех возможных пар i и j при i≠j и отнести измерение к тому классу, для которого отношение условных вероятностей имеет наибольшее значение.
Если ковариационные матрицы классов неодинаковы, то добавляется некоторая функция потерь или платежная матрица, элементами которой Rij являются значения штрафов за неправильную классификацию, когда объект х относят к классу j, когда как он принадлежит классу i. Чаще всего используют платежную матрицу R стандартного вида: ее элементы равны 0, если решающее правило правильно отнесло измерение к своему классу, и 1, если имела место ошибочная классификация. Нетрудно видеть, что при этом функционал среднего байесовского риска превращается в вероятность ошибочной классификации.
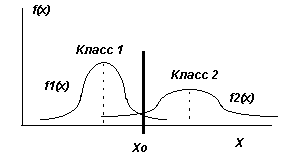
В простейшем случае для одной переменной и при двух классах процесс разделения можно представить графически на рисунке 1. Если выборки признака Х, относящиеся к обоим классам, подчинены нормальным законам распределения с дисперсией σ и средними m1 и m2, то пороговая величина х0 позволяет оптимальным образом разделить признаковое пространство на две области:
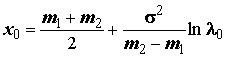 , (8.22)
, (8.22)где l0 — критическое значение коэффициента правдоподобия, который зависит от платежных коэффициентов и априорных вероятностей появления объектов первого и второго класса. Если r11=r22=0, r12=r21 и априорные вероятности равны, то l0=0 и линия х0 проходит посередине между средними обоих классов.
Формула Байеса и оптимальные параметрические решающие правила могут быть использованы, если возможна достаточно точная аппроксимация функции плотности распределения данных. Если эта аппроксимация на основе обучающей выборки недостаточно точна, то и решающая функция будет далека от оптимальной. Сложность расчетов по восстановлению условных функций распределения F(x/yi) или ее плотности р(x/yi), i=1,2,…,l, является самым большим препятствием к использованию параметрических методов в многочисленных приложениях.
Однако, когда вид кривой плотности распределения неизвестен и нельзя сделать вообще никаких предположений о ее характере, то все равно общую стратегию Байеса можно обобщить на любой непараметрический метод расчета с участием двух матриц — платежной матрицы R и диагностической матрицы P, содержащей некоторые оценки условных вероятностей отнесения объекта к каждому классу, если объект имеет определенную комбинацию признаков. Существует значительное множество различных алгоритмов формирования диагностической матрицы P, использующих разные эвристические предположения их авторов. Расчет оценок может быть основан, например, на использовании метода многомерных гистограмм (частот встречаемости в различных классах объектов обучающей выборки, содержащих тот или иной признак [Гублер, 1978]), средних мер близости для компактных подмножеств объектов [Журавлев, 1978], нормированных разностей между внутригрупповыми средними и общим средним значением признака, эвристиках Е. Парзена [Parzen, 1962] и Э.А. Надарая [1964] и т.д.
Методы линейного дискриминатного анализа
Основной целью дискриминации является нахождение такой линейной комбинации переменных, которая бы оптимально разделила рассматриваемые группы. Линейная функция
dik=a0k+a1k×xi1k+a2k×xi2k+…+ajk×xijk+…+amk×ximk, (8.23)
при i=1, 2,…,nk; k=1, 2,…, p; называется дискриминантной функцией с неизвестными коэффициентами ajk. Здесь dik — расчетное значение функции для i–го объекта из группы k, состоящей из совокупности nk измерений; xijk — значение j–й дискриминантной переменной, j=1,2,…,m — столбцы матрицы наблюдений.
В общем случае необходимо рассчитать p линейных дискриминантных функций, равное количеству анализируемых популяций, после чего с использованием коэффициентов ajk и постоянной a0k можно провести классификацию любого произвольного наблюдения. Для этого необходимо подставить значения переменных вектора х в дискриминантные уравнения для каждой k–й группы и рассчитать значения оценок отклика, k=1, 2,…, p. Вектор х классифицируется как принадлежащий тому классу (группе измерений, популяции) k, для которого величина dk имеет максимальное значение.
Для расчета коэффициентов дискриминантных функций нужен статистический критерий, оценивающий различия между группами. Очевидно, что классификация переменных будет осуществляться тем лучше, чем меньше рассеяние точек относительно центроида внутри группы и чем больше расстояние между центроидами групп. Один из методов поиска наилучшей дискриминации данных заключается в нахождении таких дискриминантных функций dk, которые были бы основаны на максимуме отношения межгрупповой вариации к внутригрупповой.
Многомерное нормальное распределение случайной величины xijk характеризуется следующими статистическими компонентами:
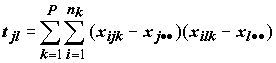 , (8.24)
, (8.24)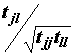 ;
;
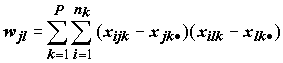 . (8.25)
. (8.25)Если расположение центров классов различается между собой, то степень вариации наблюдений внутри классов будет меньше общего статистического разброса: wjl<tjl, причем, чем больше расхождение этих величин, тем ощутимее влияния фактора группировки. Введем матрицу разницы этих двух матриц B, которая представляет собой межгрупповую сумму квадратов отклонений и попарных произведений B=T–W (т.е. bjl=tjl–wjl). Величины элементов B по отношению к величинам элементов W дают меру различия между группами.
Коэффициенты a0k, a1k, a2k,…, amk разделяющих функций могут быть найдены по методу дискриминантного анализа Фишера как элементы матрицы, обратной к W, что соответствует общей вычислительной процедуре множественной линейной регрессии. Более сложным в математическом отношении является канонический дискриминантный анализ, где ищутся независимые или ортогональные функции, вклады которых в разделение совокупностей не будут перекрываться. С вычислительной точки зрения здесь проводится анализ канонических корреляций, в котором определяются последовательные канонические корни и вектора.
Для нахождения p наборов коэффициентов канонических дискриминантных функций необходимо решить систему уравнений:
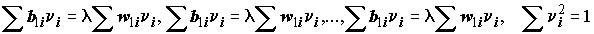 . (8.26)
. (8.26)Как известно из курса линейной алгебры, собственными значениями квадратной матрицы В порядка m называются такие значения lj, при которых система следующих m уравнений имеет нетривиальное решение:
Вnj= ljnj, j=1, 2,…, m, (8.27)
где nj собственные векторы матрицы В, соответствующие lj. Нетривиальное решение системы уравнений: Вnj=ljWnj, j=1, 2,…, m, где B и W — симметрические положительно определенные матрицы, относится к обобщенной проблеме собственных значений и может быть получено путем замены переменных, используя разложение по Холецкому.
Используя компоненты собственных векторов nj для описанных выше ковариационных матриц B и W, находят путем нормировки p наборов нормированных коэффициентов канонических дискриминантных функций ajk=njk(n–p)0.5. С геометрической точки зрения, полученные дискриминантные функции определяют гиперповерхности в m–мерном пространстве. В частном случае при m=2 они являются прямыми, а при m=3 — плоскостями. В этих обозначениях функция расстояния Махалонобиса, учитывающая расстояние между центроидами двух классов k и r, будет равна:
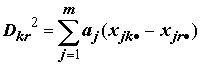 . (8.28)
. (8.28)Заключительный этап дискриминантного анализа включает методы интерпретации межгрупповых различий и методы классификации наблюдений по группам. При интерпретации нужно ответить на вопросы: возможно ли, используя данный набор переменных, отличить одну группу от другой, насколько хорошо эти переменные помогают провести дискриминацию и какие из них наиболее информативны? Детальный анализ проводится с использованием объединенной матрицы ковариации T и ковариационных матриц для отдельных групп Wk, k=1, 2,…, p.
Напомним еще раз основные предположения дискриминантного анализа. Во–первых, считается, что анализируемые переменные представляют выборку из многомерного нормального распределения. Отметим, однако, что пренебрежение условием нормальности обычно не является "фатальным" в смысле доверия к результатам расчетов. Более важно второе предположение о статистическом равенстве внутригрупповых матриц дисперсий и корреляций. При искусственном объявлении ковариационных матриц Wk статистически неразличимыми могут оказаться отброшенными наиболее важные индивидуальные черты, имеющие большое значение для хорошей дискриминации.
Так как дискриминантные функции находятся по выборочным данным, они нуждаются в проверке статистической значимости. Определяющим для дискриминантного анализа является проверка гипотезы об отсутствии различий между групповыми средними H0 : m1=m2=…=mp, что является многомерным аналогом однофакторного дисперсионного анализа. Для этого может быть использовано обобщенное расстояние Махалонобиса, которое в матричном виде можно записать как
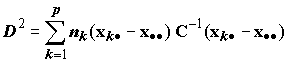 . (8.29)
. (8.29)На содержательном уровне его можно интерпретировать как взвешенную сумму расстояний от вектора средних каждой группы Xk⋅ до общего вектора средних X⋅⋅. Если гипотеза Н0 верна, а объем выборки стремится к ∞ (достаточно большой), то D2 может быть аппроксимирована F–распределением. Другим, в некоторых случаях более точным способом проверки гипотезы H0 является использование U–статистики Уилкса (она же — лямбда Вилкса), которая вычисляется как отношение детерминантов (det) матрицы внутригрупповой ковариации W и полной ковариационной матрицы Т:
Аппроксимация статистики U–Уилкса с помощью F–распределения была выполнена К. Рао.
Наиболее общим принципом применения дискриминантного анализа является включение в исследование по возможности большего числа переменных с целью определения тех из них, которые наилучшим образом разделяют выборки между собой. Для этой цели, как и в случае множественного регрессионного анализа, используется пошаговая процедура, в которой на каждом шаге построения модели дискриминации просматриваются все переменные и находится та из них, которая вносит наибольший вклад в различие между совокупностями. Эта переменная включается в модель на текущем шаге и происходит переход к следующему шагу. Можно также двигаться в обратном направлении и все переменные будут сначала включены в модель, а затем на каждом шаге будут устраняться признаки, вносящие наименьший вклад в предсказание. Пошаговая процедура дискриминантного анализа для отбора переменных основывается на F–критериях однофакторного дисперсионного анализа: "F–включения" и "F–исключения". Значение F–статистики для переменной указывает на ее статистическую значимость при дискриминации между совокупностями и является мерой вклада признака в предсказание членства в группах. Тогда в качестве результата успешного анализа можно сохранить только наиболее информативные переменные модели, то есть те переменные, чей вклад в дискриминацию больше остальных.
Другим полезным критерием, используемым для селекции признаков, является коэффициент множественной корреляции R2 для соответствующей переменной со всеми другими переменными в текущей модели. При значениях R2, близких к 1, анализируемый признак полностью определяется комбинацией других признаков и является избыточным. При сильной взаимной коррелированности переменных матрица задачи становится плохо обусловленной, что резко сказывается на погрешностях расчетов. И, наконец, дискриминантные функции представляются аналогами главных компонент, поэтому для нахождения оптимального числа переменных можно воспользоваться критериями, оценивающими остаточную дискриминантную способность, под которой понимается способность различать группы с помощью переменных, не включенных в модель. Это может быть, например, L–статистика, вычисляемая по формуле:
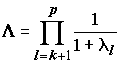 . (8.30)
. (8.30)Если остаточная дискриминация мала, то выполненный анализ достиг своей цели.
Кроме задачи "объяснения", другой главной целью применения дискриминантного анализа является задача "прогнозирования". Как только модель установлена и получены дискриминирующие функции, возникает вопрос о том, как хорошо они могут предсказывать, к какой совокупности принадлежит конкретное измерение? Обычно классификация объектов осуществляется с использованием одного из следующих методов:
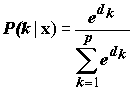 , вычисленные для каждого класса k=1, 2,…, p.
, вычисленные для каждого класса k=1, 2,…, p.На точность классификации может сильно влиять способ спецификации априорных вероятностей наблюдений в различных совокупностях. Если неодинаковая заселенность классов в первоначальной выборке является отражением истинного распределения в популяции, то необходимо положить априорные вероятности пропорциональными объемам совокупностей в выборке. Если это только случайный результат процедуры формирования обучающей выборки, то априорные вероятности принимаются одинаковыми для каждой группы.
Результаты достоверности оценки классов анализируются с использованием таблицы сопряженности "Факт—Прогноз". С помощью этой таблицы можно оценить вероятность ошибочной классификации каждого класса, которая является смещенной.
Сохранено с http://www.tolcom.ru/kiril/Library/Book1/content383/