Метод наименьших квадратов (МНК)
Источник:
http://iissvit.narod.ru/htm/vip9.htm
МНК является классическим методом, с которого надо начинать обзор о
методах прогнозирования. Приведено краткое описание данного метода и
показывается, как с помощью его строить прогнозы.
Пусть в качестве исходных данных имеем таблицу
| X |
|
|
… |
|
| Y |
|
|
… |
|
содержащую статистические данные, или данные
экспериментов. Если в качестве X выступает
время, то имеем динамический ряд (тогда
размещены в возрастающем порядке). Необходимо
получить аналитическую зависимость
, (*)
которая наилучшим образом описывает начальные
данные. Словосочетание «наилучшим образом», будем понимать в смысле минимума
суммы квадратов отклонений значений
, данных в таблице от
, рассчитанных по (*):
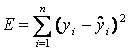
(**) Определение зависимости (*) необходимо, в т.ч., и для нахождения
, что уже
представляет собой задачу прогнозирования.
Нанесём
точки из таблицы на координатную плоскость и сделаем предположение, что
зависимость (*) есть линейной
, а
отклонения от прямой вызваны случайными факторами.
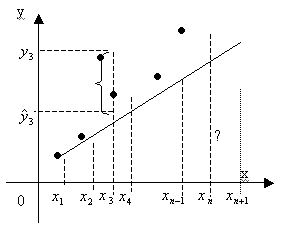
Определим уравнение прямой (найдем значения коэффициентов a и b), так, чтобы
получить решение задачи
, т.е.
необходимо найти минимум функции
.
Функция
.
Продифференцируем
по a и по b.
Получим:
,
.
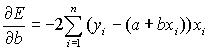Для того, чтобы найти минимум функции E(a,b), приравняем нулю производные и упростим систему:
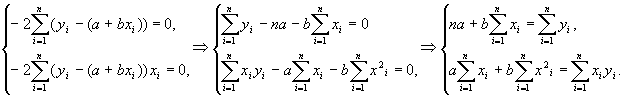
Последнюю систему можно представить в матричном виде:
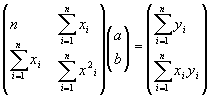
Решая её получим:
.
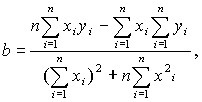
Вычислив a и b, получим функцию
, которая в
классе линейных функций наилучшим образом описывает табличную зависимость в
смысле минимума суммы квадратов отклонений. Теперь можно рассчитать и прогноз
.