6. МЕТОДИ РІШЕННЯ ЛІНЕЙНОЇ КРАЙОВОЇ ЗАДАЧИ ДЛЯ ЗВИЧАЙНИХ ДІФЕРЕНЦІАЛЬНИХ РІВНЯНЬ

Першоджерело: http://www.opu.odessa.ua/konsp/OMP/RAZDEL6/glava6.htm

  Постановка задачи

Нехай дано ЛДР другого порядку:
Y"+P(x)Y'+g(x)Y=f(x) 
(6.1) 
де P(x), g(x), f(x)-відомі неперервні на відрізку [a, b]  функції. Лінейна крайова задача для (6.1),а на його кінцях-лінейним крайовим умовам.                                                            

A0.Y(a)+A1.Y'(a)=A 
B0.Y(a)+B1.Y'(a)=B 
(6.2)
  де A0, A1, B0, B1-задані постійні,причому A0, A1, B0, B1 не дорівнюють одночасно
нулю (|A0|+|A1|№ 0; |B0|+|B1|№ )0. Якщо A=B=0,то крайові умови (6.2) називаються однорідними. Лінейна крайова задача називається однорідною,якщо однорідні ДР(1)(f(x)=0) і крайові умови (6.2).  Оскільки умови (6.2) повинні виконуватись  в двох точках - на кінцях  інтервалу [a, b],їх називають двохточечними крайовими умовами, а крайову задачу - двохточечною крайовою задачею. Точне рішення крайової задачи можливе в рідких випадках.Тому на практиці часто використовують приблизні методи рішення,які можна розбити на дві групи:
а) аналітичні;
б) різністні.
Роздивимося один із різністних методів-метод кінцевих різностей.
6.2. Метод кінцевих різностей
 
Одним із найбільш простих методів рішення лінейної крайової задачи (6.1- 6.2) являїться зведення її до системи кінцево-різностних рівнянь. Класичне знаходження похідної функції однієї змінної записується в виді:
            dY/  dX  =lim (Y(x+h)-Y(x) )/ h                 
Звичайно, на ЕОМ ми не можемо провести граничного переходу. З другої сторони, ми можемо надати h деяке мале хоч і ненульове значення і перевірити, що приближення одержуїться досить точним(проблема точності) і що помилка не збільшується в ході процесу обчислювань (проблема утриманності). Цей метод (кінцевих різностей) зводиться до того,що ми замінюємо похідну різністью. Розіб'ємо відрізок [a, b] на n рівних частин довжиною h (шаг). h=(b-a)/n
 Позначимо точки ділення відрізка [a, b]
                                          X0=a; Xn=b; Xi=X0+ih   (i=1, 2, ..., n-1);
                           Pi=P(Xi);Ji=J(Xi);fi=f(Xi);Yi=Y(Xi);Yi'=Y'(Xi);Yi"=Yi"(Xi).
Замінимо приблизно в кожній внутрішній точці Xi відрізка [a, b] похідні Yi' і Yi" кінцево- різністні відношення.
Yi'=(Yi+1-Yi)/ h  ;  
Yi"=(Yi+1-2Yi+1+Yi)/ h2
 (6.3) 
 Для граничних точок X0=a і Xn=b надамо:
Y0'=(Y1-Y0)/ h ; 
Yn'=(Yn-Yn-1 )
 (6.4)
Використовуючи формули (6.3) і (6.4), приблизно замінимо рівняння (6.1) і крайові умови (6.2) системою n+1 лінейних алгебраїчних рівнянь з n+1 невідомими Y0,Y1,Y2,...,Yn, які являють собою значення шуканої функції Y=Y(x) в точках  X0,X1,X2,...,Xn:
(Yi+2-2Yi+1+Yii )/ h2+Pi(Yi+1-Yi)/ h +giYi=Fi; 
( i=0, 1, 2, ..., n-2) 
A0Y0+A1(Yi-Y0)/ h=A; 
B0Yn+B1(Yn-Yn-1)/ h=B;
(6.5)
Розв'язавши цю систему, можна одержати таблицю приблизних значень шуканої функції Y=Y(x).
На практиці часто похідні Yi' і Yi" в внутрішніх точках Xi відрізка  [a, b] замінюють центрально-різностними відношеннями:
Yi'=(Yi+1-Yi-1)/2h ; 
Yi"=(Yi+1-2Yi+Yi-1)/h2 .
 (6.6)
а для граничних точок X0=a і Xn=b також справжні формули (6.4). Тоді система  рівнянь для находження Y0, Y1, ... ,Yn приймаї вид:
 (Yi+2-2Yi+1+Yi )/h2 +Pi(Yi+1-Yi )/2h+giYi=Fi; 
( i=0, 1, 2, ..., n-1) 
A0.Y0+A1(Yi-Y0)/h=A; 
B0.Yn+B1(Yn-Yn-1 )/h=B 
(6.7)
Для оцінки похибки метода кінцевих різниць на практиці часто використовують слідуючий приблизний вираз:
Yi*-Y(xi)=1/3 [Yi*-Yi]
(6.8) 
де Y(xi)-значення точного рішення крайової задачи в точці X=Xi;
    Yi -значення приблизногорішення,обчисленного в точці X=Xi з кроком h ;
    Yi*-значення приблизного рішення,обчисленного в точці X=Xi з кроком h/2;
Щоб знайти приблизне рішення крайової задачи з заданною точністю Є, необхідно провести обчислювання з кроком h і h/2  b зрівняти полученні  результати. Якщо [Yi* -Yi]<3ЧE, то, з цього випливає, [Yi* -Yi]<Є і значення  Yi* (i=1,2,...,n) можна прийняти за рівняння краївої задачи.
 
6.3 Метод прогонки

        При великому n безпосереднє рішення систем (6.5) або (6.7) стає дуже нагромадженним. Для рішення систем такого виду було розроблено спеціальний метод,який отримав назву метода прогонки. Нехай маємо систему (6.5). Розглянемо перше n-1 рівняння
(Yi+2-2Yi+1+Yi )/h2+Pi(Yi+1-Yi )/h+giYi=Fi; 
 (i=1, 2 ,..., n-1) 
Переобразовуючи , отримуємо:
Yi+2+(-2+hPi)Yi+1+(1-hPi+h gi)Yi=h Fi
(6.10)
Введемо позначення :
Mi= -2+hPi; Ki=1-hPi+h2 gi,   (i=0, 1, 2,..., n-2) 
 (6.11)
Тоді (6.10) замінюємо в виді:
  Yi+2+MiYi+1+KiYi=hFi 
(6.12)
Розв'язавши (6.12) відносно Yi+1, одержимо:
Yi+1= h2Fi/Mi -Yi+2/Mi - KiYi/ Mi 
(6.13)
Нетяжко впевнитися в тому, що, вийнявши Yi із (6.13) з допомогою крайових умов системи (6.5), одержимо це рівняння в виді:
Yi+1=Ci(di -Yi+2)  
(i=0, 1, 2,..., n-2) 
 (6.14) 
де Ci,di - деякі коефіціїнти. Нехай ,наприклад, i=0; тоді (6.13) прийме вид:
Y1=h Fi/M0 -Y2/M0 - K0Y0/M0 ;
(6.15)
Із крайової умови A0Y0+A1( Y1-Y0 )/h =A  найдемо Y0:
Y0 =Ah /(A0-h)-A1Y1/(A0h-A1)
і підставимо його в (6.15). Після преобразовувань одержимо :
Позначимо:
   
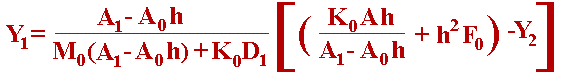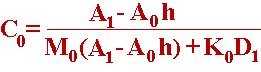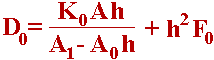(6.16)
Із (6.14) можна записати:
        Yi=Ci-1(di-1-Yi+1)
Підставляючи цей вираз в (6.12), одержимо :
        Yi+2+MiYi+1+KiCi-1(di-1-Yi+1)=h .Fi
Звідкіля:
Yi+1=[(h Fi-KiCi-1Di-1)]/(Mi-KiCi-1)
(6.17)
Зрівнюючи (6.14) і (6.17), одержимо для знаходження Ci і Di рекурентні формули:
Ci=1/(Mi-KiCi-1); Di=hFi-KiCi-1Di-1; 
  де i=1, 2, ..., n-2;
      Ci,Di- прогоночні  коефіцієнти. Метод прогонки полягає з двох етапів: прямого і зворотнього ходу. На першому етапі (прямий хід) на основі (6.16) знаходжуються коефіцієнти
C0 і D0. Після цього, послідовно використовуючи рекурентні формули (6.18) одержують значення Ci і Di (i=1, 2, ..., n-2). Другий етап (зворотний хід) починається з знаходження Yn.Використовуючи другу крайову умову (6.5) і формулу (6.14) при і= п-2, запишимо систему другорядних рівнянь:
B0Yn+B1(Yn-Yn-1)=B ; 
Yn-1 = Cn-2(dn-2-Yn); 
(6.19)
Розв'язавши цю систему відносно Yn,одержимо:
Yn-1 =(B1Cn-2Dn-2 + Bh)/[ B1(1 + Cn-2) + B0h ]
(6.20)
Підставивши в (6.20) уже знайдені прямим ходом Сп-2,Dn-2,знаходимо Yn. Після цього обчислюють Yn-1, Yn-2, Yn-3, ..., Y1,послідовно використовуючи рекурентну формулу (6.14):
    Yn-1 = Cn-2(Dn-2 - Yn); 
    Yn-2 = Cn-3(Dn-3 - Yn-1); 
                ...............          ; 
    Y1 = C0(D0 - Y2)  ;
(6.21)
    Значення Y0 знаходимо по формулі,яка була одержана з першої крайової умови (6.5) :
Y0=(A1Y1 - Ah )/(A1 - A0h )
(6.22)