Володин Н.А., Толстых В.К.
О применении градиентного метода оптимизации к задаче теплового управления реактором

Первоисточник: Володин Н.А., Толстых В.К. О применении градиентного метода оптимизации к задаче теплового управления реактором // Журн. Автоматика, 1993., №1, с. 40-44.

Настоящая работа посвящена развитию градиентного подхода к задачам оптимизации систем с распределенными параметрами применительно к задачам оптимального управления нестационарными уравнениями параболического типа.

Примем в качестве объекта исследований химический реактор. Пусть реакция в нем протекает с поглощением тепла q. Весь процесс должен удовлетворять экстремальному температурному режиму Т_э(t) реакции на внутренней поверхности стенок реактора. Управление температурой реакции будем осуществлять регулировкой потока тепла u(t) на внешней поверхности стенок. При этом процесс теплопередачи запишется в виде:

где а, c - коэффициенты температуро- и теплопроводности соответственно, Т_а - начальная температура стенок.

Степень отклонения температуры Т(t,x₀) реакции от заданной экстремальной температуры будем оценивать функционалом

Задача оптимального управления реактором формулируется следующим образом. Необходимо найти поток тепла u(t), доставляющий минимум функционалу J.

По техническим соображениям могут присутствовать ограничения на скорость ввода тепла с закрепленностью нулевого начального потока:

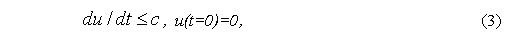
и на минимальную температуру стенок реактора (условие незамерзания реактора):

Следуя градиентному подходу к задачам оптимизации систем с распределенными параметрами может быть найден градиент функционала (2):

где f(t,x) - множитель Лагранжа, удовлетворяющий сопряженной задаче:

На основе градиента (5) организуется направленная итерационная коррекция управления:

где k - номер итерации, a - параметр шага градиентного спуска.

Особенностями задачи является наличие ограничений (3), (4) и недифференцируемость функционала (2) при управлении, обеспечивающем экстремальный температурный режим T=T_э. Такое управление называется сингулярным.

Согласно градиентному подходу попадание в граничные, стационарные (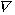J=0) в сингулярные точки (подразумеваются точки функциональных пространств) на основе алгоритма (7) является необходимым условием оптимальности, более того, для граничных точек оно является и достаточным. Следовательно, решение по градиентному алгоритму (7), приводящее к ограничениям (3), (4), будет заведомо оптимально.

Достаточное условие оптимальности для не граничных точек требует дополнительной проверки: при переходе по алгоритму (7) через управление, подозреваемое на локальный минимум, градиент (5) должен менять свой знак почти во все моменты времени. Данная проверка при функционале (2) организуется автоматически при выборе параметра шага коррекции следующим образом:

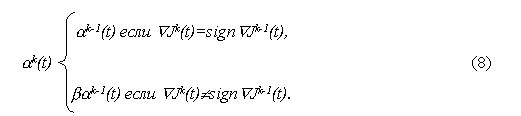
Коэффициент 0<b<1. После каждого перехода через сингулярное управление на различных подмножествах из (t_a, t_b) происходит более медленное приближение к оптимальному решению с противоположной стороны. С увеличением возрастает скорость сходимости, но может нарушаться устойчивость.

Градиентный метод позволяет просто и наглядно реализовывать многие ограничения на управление. Так, ограничение (3) на скорость изменения управления в алгоритме (7) реализуется проецированием на границу du/dt=c управления u^k+1(t) на соответствующих подмножествах из (t_a,t_b) нарушения данного ограничения:

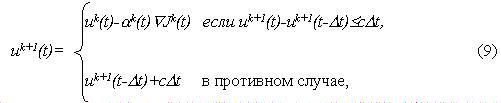
где Δt - временной шаг решения задачи. Закрепленность начального нулевого потока тепла реализуется смещением всего управления относительно его начального значения:

Ограничение (4) на состояние процесса теплопередачи может быть учтено различными способами. Наиболее распространенные - это методы штрафных функционалов. Однако они не позволяют отыскивать точные решения, поскольку либо "штрафуют" все решения на значительном расстоянии от границы ограничения, либо допускают нарушения ограничений. Точная минимизация функционала при строгом выполнении ограничения на состояние может быть реализована следующим образом.

Пусть u^k(t) таково, что T^k(t,x) удовлетворяет ограничению (4), а u^k+1(t) приводит к тому, что T^k+1(t,x) выходит за данное ограничение на некотором пространственно-временном множестве S_outS с элементами (t_out, x_out). Для каждой точки (t_out, x_out) нарушения ограничения (4) значение состояния T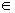R(t_out, x_out) зависит от управления u(t)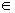H(S_inf) определенного не в точке, а на множестве S_inf=x₁X(t_a,t_out) влияния управления на данное нарушения ограничения (4). Здесь R(t_out, x_out) и H(S_inf) числовое и функциональное пространство соответственно. Верхняя граница множества S_inf определяется временем t_out вследствие бесконечной скорости распространения возмущений в параболических уравнениях: dx/dt=±.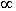

Теперь обратимся к геометрической интерпретации градиентного подхода в связи с рассматриваемым ограничением. На рис. 1 в плоскости R(t_out, x_out)XH(S_inf) линии T(u) соответствует уравнение (1). Алгоритм минимизации выглядит следующим образом. Пусть имеется u^k приближение управления. Решая уравнение (1), мы попадаем в точку A(T^k,u^k). Из решения сопряженной задачи (6) находим в этой точке градиент 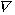J^k. Далее по алгоритму (7) продвигаемся с шагом α^k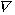J^k против градиента и попадаем на линию u^k+1. Снова решая уравнение (1), мы попадаем в точку B(T^k+1, u^k+1). При появлении ограничения на температуру данный алгоритм нарушается. Теперь задача состоит в том, чтобы при переходе от точки А к точке В задержаться в точке С.

Из рис.1 следует соотношение:

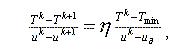
где u_d - управление, соответствующее температуре T_min, 0<η<=1 - коэффициент коррекции для нелинейных уравнений. В данном случае принималось η=1.

Учтя выражение (7), преобразуем данное соотношение к виду:

u_d=u^k-a_da^k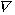J^k, t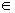US_inf(t_out), (11)

Алгоритм (11) означает, что для каждого момента времени t, принадлежащего объединению всех множеств влияния S_inf, должна осуществляться коррекция управления с дополнительным параметром α_d шага, градиентного спуска. Поскольку при этом для каждого момента времени t_out нарушения ограничения (4) возможно пересечение различных множеств S_inf, то естественно, что на их пересечение необходимо брать минимальное из имеющихся здесь значений α_d. Заметим, что при вычислении параметра α_d(t_out) координата x_out не играет никакой роли в виду мгновенности распространения возмущений.

Начиная с итерации, приведшей к нарушению ограничения (4), алгоритм (7) через каждую последующую итерацию будет на US_inf заменяться алгоритмом (11). Такой метод минимизации строго выполняет ограничение и не "штрафует" решение внутри ограничения.

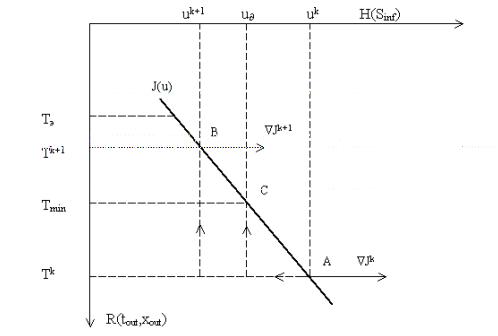
Рис. 1.