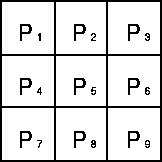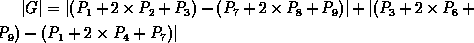R. Fisher, S. Perkins, A. Walker and E. Wolfart. Published by J. Wiley & Sons, Ltd. 1996.
Sobel Edge Detector
Brief Description
The  Sobel operator
performs a 2-D spatial gradient measurement on an image and so emphasizes
regions of high
spatial frequency that correspond to edges. Typically it is used to find the
approximate absolute gradient magnitude at each point in an input grayscale
image.
Sobel operator
performs a 2-D spatial gradient measurement on an image and so emphasizes
regions of high
spatial frequency that correspond to edges. Typically it is used to find the
approximate absolute gradient magnitude at each point in an input grayscale
image.
How It Works
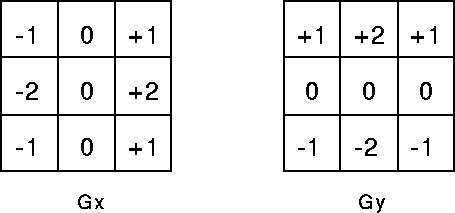
In theory at least, the operator consists of a pair of 3×3 convolution kernels as shown in Figure 1. One kernel is simply the other rotated by 90°. This is very similar to the Roberts Cross operator.
Figure 1 Sobel convolution kernels
These kernels are designed to respond maximally to edges running vertically and horizontally relative to the pixel grid, one kernel for each of the two perpendicular orientations. The kernels can be applied separately to the input image, to produce separate measurements of the gradient component in each orientation (call these Gx and Gy). These can then be combined together to find the absolute magnitude of the gradient at each point and the orientation of that gradient. The gradient magnitude is given by:
Typically, an approximate magnitude is computed using: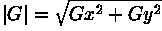
which is much faster to compute.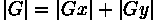
The angle of orientation of the edge (relative to the pixel grid) giving rise to the spatial gradient is given by:
In this case, orientation 0 is taken to mean that the direction of maximum contrast from black to white runs from left to right on the image, and other angles are measured anti-clockwise from this.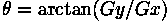
Often, this absolute magnitude is the only output the user sees --- the two components of the gradient are conveniently computed and added in a single pass over the input image using the pseudo-convolution operator shown in Figure 2.
Figure 2 Pseudo-convolution kernels used to quickly compute approximate gradient magnitude
Using this kernel the approximate magnitude is given by:
Guidelines for Use
The Sobel operator is slower to compute than the Roberts Cross operator, but its larger convolution kernel smooths the input image to a greater extent and so makes the operator less sensitive to noise. The operator also generally produces considerably higher output values for similar edges, compared with the Roberts Cross.
As with the Roberts Cross operator, output values from the operator can easily overflow the maximum allowed pixel value for image types that only support smallish integer pixel values (e.g. 8-bit integer images). When this happens the standard practice is to simply set overflowing output pixels to the maximum allowed value. The problem can be avoided by using an image type that supports pixel values with a larger range.
Natural edges in images often lead to lines in the output image that are several pixels wide due to the smoothing effect of the Sobel operator. Some thinning may be desirable to counter this. Failing that, some sort of hysteresis ridge tracking could be used as in the Canny operator.