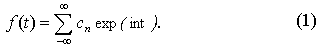
Wavelet-analysis - a new method for time lines analysis is examined. Review of major mathematical ideas and outputs of wavelet-transformations is given. Some specific applications to the apparatus are shown.
Традиционно для анализа временных рядов используется преобразование Фурье, дающее разложение исследуемого временного процесса f(t) в ряд по тригонометрическим функциям, или в более общей форме записи
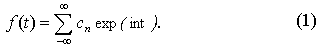
Коэффициенты сn являются амплитудами гармонических колебаний соответствующей частоты.
Множество функций exp(int) образует ортонормированный базис пространства L2(0,2p).
Аппарат Фурье-преобразований дает достаточно простые для расчетов формулы и прозрачную интерпретацию результатов, но не лишен и некоторых недостатков. Преобразование, например, не отличает сигнал, являющийся суммой двух синусоид, от ситуации последовательного включения синусоид, не дает информации о преимущественном распределении частот во времени, может дать неверные результаты для сигналов с участками резкого изменения. Исследуемые ряды также далеко не всегда удовлетворяют требованию периодичности и более того, как правило, заданы на ограниченном отрезке времени.
Основы вейвлет-анализа были разработаны в середине 80-х годов Гроссманом и Морле как альтернатива преобразованию Фурье для исследования временных (пространственных) рядов с выраженной неоднородностью. В отличие от преобразования Фурье, локализующего частоты, но не дающего временного разрешения процесса, и от аппарата d-функций, локализующего моменты времени, но не имеющего частотного разрешения, вейвлет-преобразование, обладающее самонастраивающимся подвижным частотно-временным окном, одинаково хорошо выявляет как низко-частотные, так и высокочастотные характеристики сигнала на разных временных масштабах. По этой причине вейвлет-анализ часто сравнивают с "математическим микроскопом", вскрывающим внутреннюю структуру существенно неоднородных объектов.
Указанная универсальность обеспечила вейвлет-анализу широкое использование в самых различных областях знаний. Семейства анализирующих функций, называемых вейвлетами, применяются при анализе изображений различной природы, для изучения структуры турбулентных полей, для сжатия больших объемов информации, в задачах распознавания образов, при обработке и синтезе сигналов, например, речевых, для определения характеристик фрактальных объектов.
Подобно тому, как в основе аппарата преобразований Фурье лежит единственная функция w(t)=exp(it), порождающая ортонормированный базис пространства L2(0,2p) путем масштабного преобразования, так и вейвлет-преобразование строится на основе единственной базисной функции y(t), имеющей солитоноподобный характер и принадлежащей пространству L2(R), т.е. всей числовой оси.
В западной литературе за этой функцией закрепилось название "вейвлет", что означает "маленькая волна", в отечественной иногда ее называют "всплеском", отражая в этом названии и локализацию, и осцилляционный характер поведения.
При конструировании базисной анализирующей функции y(t) должны выполняться следующие необходимые условия.
Локализация - вейвлет должен быть локализован вблизи нуля аргумента как во временном, так и в частотном пространстве.
Как следствие, вейвлет должен быть знакопеременной функцией.
Вейвлет должен быть достаточно быстро убывающей функцией временной (пространственной) переменной.
Базис одномерного дискретного вейвлет-преобразования (ДВП) строится на основе вейвлета y(t) посредством операций сдвигов и растяжений вдоль оси t. Вводя аналог синусоидальной частоты и принимая для простоты в качестве ее значений степени двойки, получаем для функций базиса yjk(t)= 2j/2y(2jt-k)
Базис нормирован, если вейвлет имеет единичную норму.
Вейвлет называется ортогональным, если семейство {yjk} представляет ортонормированный базис функционального пространства L2(R), т.е. <yjk,ylm>=djl dkm. В этом случае любая функция fО L2(R) может быть представлена в виде ряда
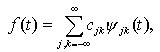
где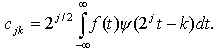
Непрерывное вейвлет-преобразование (НВП) строится аналогичным образом с помощью непрерывных масштабных преобразований и переносов вейвлета y(t) с произвольными значениями масштабного коэффициента a и параметра сдвига b.
Вейвлет-преобразование обратимо для функций f из L2(R)
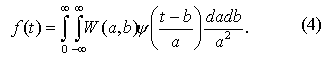
Таким образом, любая функция из L2(R) может быть представлена суперпозицией масштабных преобразований и сдвигов базисного вейвлета с коэффициентами, зависящими от масштаба (частоты) и параметра сдвига (времени).
Двухпараметрическая функция W(a,b) дает информацию об изменении относительного вклада компонент разного масштаба во времени и называется спектром коэффициентов вейвлет-преобразования.
Скейлограмма соответствует спектру мощности Фурье-преобразования сигнала, сглаженному на каждом масштабе спектром Фурье анализирующего вейвлета.
Примеры часто используемых вейвлетов
| HAAR - вейвлет: | |
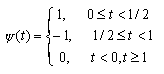 |
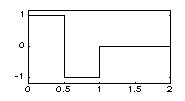 |
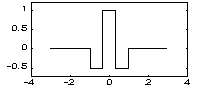
| FHAT - вейвлет ("Французская шляпа" - French hat): | |
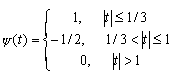 |
 |
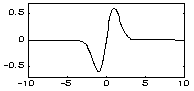
| Wave - вейвлет: | |
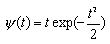 |
 |
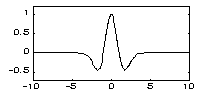
| MHAT - вейвлет ("Мексиканская шляпа" - Mexican hat): | |
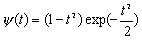 |
 |
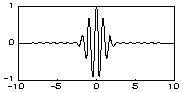
| Вейвлет Морле (образует комплексный базис): | |
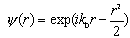 |
 |
На практике чаще приходится иметь дело с сигналами, заданными не аналитическими функциями, а с дискретным набором данных, определенном на конечном временном интервале. В этом случае принимается, что при tk£t<tk+1, f(t)=sk, k=1,2,...,n.
Выше приведены примеры часто используемых вейвлетов (см. таблицу). Выбор того или иного класса анализирующих функций диктуется спецификой задачи, тем, какую информацию нужно извлечь из сигнала. В ряде случаев с помощью различных вейвлетов можно более полно выявить особенности анализируемого сигнала.
Спектр вейвлет-преобразования одномерного сигнала представляет поверхность в трехмерном пространстве. Обычно изображение спектра выполняется путем проектирования линий постоянного уровня поверхности на плоскость с переменными: параметрами сдвига (по оси абсцисс) и масштабом (по оси ординат), с градиентной заливкой оттенками серого цвета между линиями. В данной работе выбран вариант закраски, при котором область максимума имеет белый цвет, а минимума - черный. Используется также метод представления структуры спектральных данных с помощью "скелетона" - линий локальных экстремумов поверхности W(a,b) .
На приведенных ниже графиках представлены результаты расчета спектров вейвлетпреобразования временных рядов, построенных на основе функциональных зависимостей. Ряды рассчитывались на конечном интервале времени. В качестве анализирующего вейвлета использовался MHAT-вейвлет. Верхняя часть рисунка - исследуемый сигнал, средняя - изолинии поля W(a,b), нижняя - скелетон спектра. Изображены как линии локального максимума, так и минимума. В седловых точках поверхности происходит слияние линий.
Сигнал, представленный на рис. 1, является простым гармоническим колебанием. Картина линий уровня указывает на периодический характер сигнала и в мелкомасштабной области представляет регулярную систему ячеек с поочередно повторяющимися значениями максимума и минимума поля W(a,b), положение которых соответствует максимумам и минимумам сигнала. Граница раздела ячеек совпадает с положением нулей f(t).
Как отмечалось, география приложений вейвлет-анализа очень разнообразна. Анализ рядов событий течения Эль-Ниньо и изменений индекса Южного колебания, позволил выявить периодические компоненты процессов и временные масштабы, на которых данные имеют автомодельную структуру [1]. В [2] на основе вейвлет-анализа выявлена существенная многомасштабность временных колебаний среднегодовой глобальной температуры воздуха за последние 150 лет и получены количественные оценки параметра Херста. Делается вывод о некорректности использования традиционных средств тестирования стационарных случайных процессов без предварительного разделения колебаний на нестационарную (тренд) и осцилляторную части при изучении современных изменений климата. Прогнозируется возможная приостановка дальнейшего роста глобального потепления или, по крайней мере, его замедление. Хорошая подборка статей для начального знакомства с идеями, аппаратом и применением вейвлет-преобразований опубликована в журнале [3], где даются ссылки и адреса в сети материалов по теории и приложениям вейвлет-анализа.
Одним из направлений приложений вейвлет-анализа является исследование свойств фрактальных объектов различной природы и, в частности, определение фрактальной размерности. Скелетон вейвлет-преобразования показывает наличие скрытого самоподобия в непрерывном отображении или дискретном наборе данных в виде развитой древообразной структуры с развилками, зависящими от масштаба по степенному закону.
Для временных рядов показатель степени мультифрактальности можно оценить, используя метод, приведенный в [2]. Подсчитывается число точек максимумов коэффициентов вейвлет-преобразования вдоль параметра сдвига в области масштаба, где имеется выраженная ветвистая структура скелетона (обычно это интервал a =1÷16, если принять временной шаг равным 1). Тангенс угла наклона прямой линии, аппроксимирующей зависимость lnN(a)/lna методом наименьших значений, дает показатель самоподобия (в [2] для него принято название параметра Херста по имени автора, исследовавшего структуру дельты Нила).
Указанный подход использовался нами при вейвлет-анализе временных рядов отклонений температуры от среднемесячных значений по результатам измерений на метеорологической станции Фрунзе (Бишкек) за период 1931-1998 гг. (рис. 8). Оказалось, что значение параметра Херста Н = 0,9 близко к значению, приведенному в [2] и рассчитанному по той же методике (Н = 0,81). Полученные близкие значения параметра Херста на разных временных рядах разной продолжительности позволяют высказать предположение, что динамическим системам, какой, в частности, является климатическая, присущи скрытые внутренние характеристики, статистически воспроизводимые на различных временных масштабах.
Литература
1. Астафьева Н.М. Вейвлет-анализ: основы теории и примеры применения //УФН. - 1996. - Т.166. - № 11. - С. 1145-1170.
2. Сонечкин Д.М., Даценко Н.М., Иващенко Н.Н. Оценка тренда глобального потепления с помощью вейвлетного анализа // Изв. РАН. Физика атмосферы и океана. - 1997. - Т.33. - № 2. - С.184-194.
3. Компьютерра. - 1999. - № 8.
| Вернуться на главную |