С каждым годом увеличиваются размеры грузовых и пассажирских перевоз, а следовательно, растет и интенсивность движения в городах. Характерной особенностью движения является неравномерное распределение транспортных потоков во времени. В течение суток образуются периоды максимальной концентрации движения, так называемые часы пик. Именно на эти часы необходимо рассчитывать все транспортные сооружения.

       Основные недостатки сети автомобильных дорог, которые отражаются на работе автомобильного транспорта - недостаточная ее протяженность, неравномерное размещение, а также недостаточно удовлетворенные транспортно-эксплуатационные показатели. Однако перечисленные недостатки отражают лишь качественную сторону вопроса. Эффективное решение проблемы требует численного выражения требований автомобильного транспорта: сколько и в какие сроки нужно построить или реконструировать дороги, где их нужно строить и каковы должны быть их транспортно-эксплуатационные показатели.

       Для решения данной проблемы возникла необходимость создания компьютеризированной системы, основной задачей которой будет анализ транспортных потоков, оценка перспективной интенсивности и поиск решений по оптимальному устройству автомобильный дорог и дорожных развязок (перекресток, круговое движение, развязки в разных уровнях).

       Одной из самых интересных работ в данной области можно назвать статью Семенов В.В. "Математическое моделирование динамики транспортных потоков мегаполиса". В статье приводится два основных подхода сложившихся в моделировании уличного движения: детерминистический и вероятностный (стохастический). В основе детерминированных моделей лежит функциональная зависимость между отдельными показателями, например, скоростью и дистанцией между автомобилями в потоке. В стохастических моделях транспортный поток рассматривается как вероятностный процесс. [1]

       Все модели транспортных потоков можно разбить на три класса: модели-аналоги, модели следования за лидером и вероятностные модели.

       В моделях - аналогах движение транспортных средств уподобляется какому либо физическому потоку (гидро- и газодинамические модели).

       В моделях следования за лидером существенно предположение о наличии связи между перемещением ведомого и головного автомобиля. По мере развития теории в моделях этой группы учитывалось время реакции водителя, исследовалось движение на много полосных дорогах, изучалась устойчивость движения.

       В вероятностных моделях транспортный поток рассматривается как результат взаимодействия транспортных средств на элементах транспортной сети. В связи с жестким характером ограничений сети и массовым характером движения в транспортном потоке складываются отчетливые закономерности формирования очередей, интервалов загрузок по полосам дороги и т.п. [4]

       На мой взгляд наиболее интересными являются вероятностные модели. Они наилучшим образом отражают поведения автотранспорта на дорогах.

       В данной статья будет рассматриваться поведение транспортного потока на перекрестке. Одной из основных задач является определении длины очереди (величины пробки на перекрестке), а также время простоя (время отсутствия автомобилей на дороге). Проблема оценки и прогнозирования интенсивности движения в данной работе не рассматривается. Эта проблема требует отдельного анализа и в рамки данной статьи не включена. Интенсивность для всех машин принята одинаковой и равной &lambda

       Рассмотрим пересечение двух дорог с односторонним движением. Пусть

• T_цс - полный цикл светофора (начиная с зеленого);
• T_зс - время горения зеленого света светофора;

       Предположим, что когда для одной полосы загорается красный свет, зеленый свет для второй полосы загорается спустя некоторое время, чтобы "проскочивший" автомобили успели проехать.

        Поток автомобилей является простейшим потоком однородных событий. Поэтому вероятность p_k(t) наступления событий за интервал времени t выражается законом распределения Пуассона.

    ,(15)

        где λ - плотность или интенсивность потока ( λ>0 ); в простейшем случае предположим, что она постоянна и равна некоторой известной величине.[2]

       Рассмотрим движение автомобилей на перекрестке. Автомобили, поступающие в систему, либо пересекают перекресток (получают обслуживание как запросы), если проезд свободен и горит зеленый свет, либо становятся в очередь у перекрестка. Предположим, что водители не едут на красный свет, даже если на пересекающей полосе пусто.

       Обслуживание автомобиля представляет собой проезд через точку А. В рамках данной модели, примем это время одинаковым для всех автомобилей и равным . Исходя из вышеизложенного, следует вывод, что поведение транспортного потока на перекрестке можно описать с помощью одноканальной системы массового обслуживания (СМО).

       Блок - схема, иллюстрирующая движение автомобильного транспорта через перекресток, за определенное количество циклов светофора (n) представлена на рисунке - 2.

Рисунок - 2 Блок - схема, иллюстрирующая движение автомобильного транспорта через перекресток.

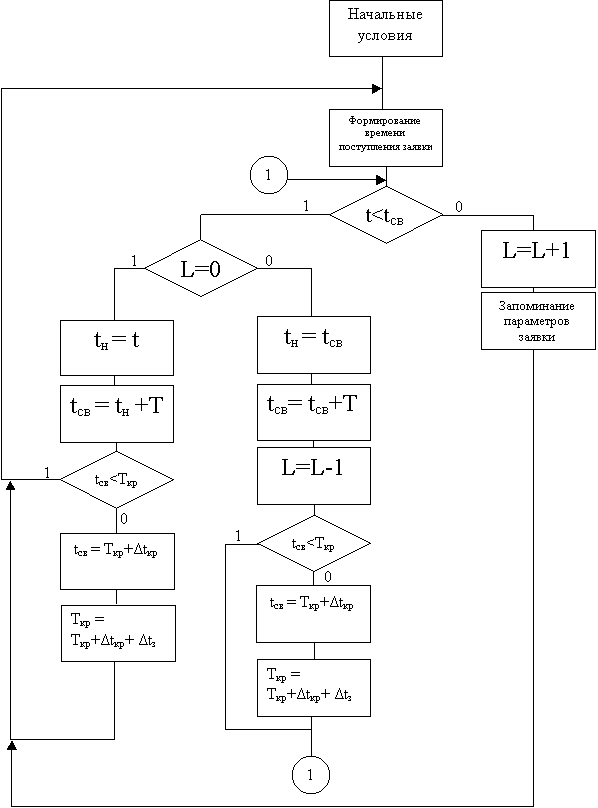
Условные обозначения:

• τ_j - промежутки времени, через которые к перекрестку подъезжают автомобили. Случайная величина, подчинающаяся закону Пуассона;
• t_j - время появления j-го автомобиля на перекрестке;
• T_цс - полный цикл светофора (начиная с зеленого);
• T_зс - время горения зеленого света светофора;
• t_св - время освобождения проезда на перекрестке;
• t_н - время выезда автомобиля на перекресток (начало обслуживания);
• T - время проезда через перекресток (время обслуживания). Для всех автомобилей принимается одинаковым;
• L - длина очереди (количество автомобилей перед светофором);
• n - количество циклов светофора.

       Как видно их блок схемы автомобиль, который подъезжает к перекрестку может либо проехать его (если горит зеленый свет), либо стать в очередь (если горит красный или проезд закрыт другими машинами). Также принято, что время ожидания у автомобиля неограниченно, т.е. он будет неограниченное количество время ждать, пока не освободится проезд.

       В заключении данной статьи следует отметить, что данный метод является не единственным возможным вариантом, но на мой взгляд наиболее приемлемым. Совмещая в себе простоту и точность, он позволяет оценить основные характеристики транспортных потоков. В дальнейшем планируется его использования для моделирования динамики транспортных потоков при круговом движении, и также на развязках в разных уровнях.

       Литература

       1. Брайловский Н.О., Грайновский Б.И. Моделирование транспортных систем - М:, Транспорт, 1978 - 125с.

       2. Бусленко Н.П. Моделирование сложных систем - М.: Наука, 1978.

       3. Дубровин Е.Н. Пересечение в разных уровнях на городских магистралях. - М.: 1968. - 278с.

       4. Семенов В.В. Математическое моделирование динамики транспортных потоков мегаполиса. http://spkurdyumov.narod.ru/Mat100.htm#Ma316.

       5. Сильянов В. В. Теория транспортных потоков в проектировании дорог и организации движения. - М.: Транспорт, 1977. - 303 с.