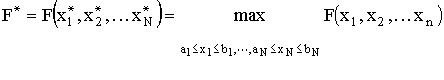
На практике подчас сложно, а порой и невозможно, зафиксировать свойства функциональной зависимости выходных параметров от входных величин, еще сложнее привести аналитическое описание такой зависимости. Это обстоятельство значительно затрудняет применение на стадии проектирования классических методов оптимизации, поскольку большинство из них основывается на использовании априорной информации о характере поведения целевой функции, а задача определения принадлежности функции тому или другому классу сопоставима по сложности с исходной. В связи с этим встает задача построения таких методов оптимизации, которые были бы способны отыскивать решения практически при полном отсутствии предположений о характере исследуемой функции. Одними из таких методов являются так называемые эволюционные методы поиска и, в частности, генетические алгоритмы (ГА), моделирующие процессы природной эволюции.
В данной работе рассматривается один из таких генетических алгоритмов для решения многопараметрической непрерывной задачи оптимизации.
Нами использована отличная от традиционной символьная модель, позволяющая манипулировать более короткими хромосомными наборами. Предлагаются новые генетические операторы, использующие специфику такой модели. Обсуждаются вопросы, связанные с влиянием операторов и значений параметров на поведение генетического алгоритма. Проведен вычислительный эксперимент с использованием традиционных для генетических алгоритмов задач.
Рассматривается непрерывная многопараметрическая задача оптимизации
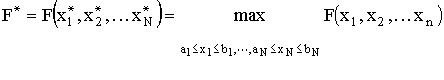
В этой задаче дифференцируемость, непрерывности, удовлетворение условию Гельдера (в том числе липшицируемость функции) не являются необходимым свойством рассматриваемого класса задач, кроме того, целевая функция может быть вовсе не определена вне допустимой области, а внутри допустимой области иметь несколько глобальных экстремумов.
Можно выделить, по крайней мере, три класса задач, которые могут быть решены представленным алгоритмом. Во-первых, это задача быстрой локализации одного оптимального решения; во-вторых, при определенных условиях, возможно отыскание нескольких (или всех) глобальных экстремумов; и в-третьих, это возможность использования алгоритма для отображения ландшафта исследуемой функции.
Генетические алгоритмы являются одними из эволюционных алгоритмов, применяемых для поиска глобального экстремума функции многих переменных. Принцип работы генетических алгоритмов основан на моделировании некоторых механизмов популяционной генетики: манипулирование хромосомным набором при формировании генотипа новой биологической особи путем наследования участков хромосомных наборов родителей (кроссинговер), случайное изменения генотипа, известное в природе как мутация. Другим важным механизмом, заимствованным у природы, является процедура естественного отбора, направленная на улучшение от поколения к поколению приспособленности членов популяции путем большей способности к "выживанию" особей, обладающих определенными признаками.
Реализацию базового генетического алгоритма можно представить как итерационный процесс, включающий несколько этапов:
Оценка качества предлагаемого алгоритма и частных генетических операторов проводилась по нескольким направлениям: во-первых, сравнение эффективности поиска в зависимости от выбранной символьной модели, в том числе от длины хромосомного набора; во-вторых, зависимость улучшения значения приспособленностей особей популяции от параметров ГА, прежде всего метода выбора родительских пар и реализации механизма отбора. Кроме того, помимо количественных оценок приводится качественное описание поведения популяции, управляемой ГА при тех или иных параметрах.
Оценка предлагаемого алгоритма проводилась на ряде тестовых функций. Это прежде всего несколько тестовых функций De Jong'а, которые часто используются для проверки эффективности новых генетических алгоритмов , кроме того, были использованы сложные многоэкстремальные функции высокой размерности, практически нерешаемые классическими методами.
| № п/п | Тестовая задача | Размерность | Свойства |
|---|---|---|---|
| 1 | De Jong 2 | 2 | Овражная функция, один глобальный экстремум |
| 2 | De Jong 3 | 5 | Разрывы типа "скачек", максимум достигается на гиперкубе |
| 3 | De Jong 5 | 2 | Один глобальный на гиперкубе, 24 локальных максимума |
| 4 | Растригина | 2 | 96 локальных экстремумов и 4 глобальных |
| 5 | Griewank | 2 | Один глобальный и множество локальных максимумов |
| 6 | Растригина | 10 | Один глобальный экстремум и 1010-1 локальных |
| 7 | Griewank | 10 | Один глобальный и множество локальных максимумов |
Более подробно используемые тестовые функции представлены в приложении.
При построении символьной модели множество допустимых решений представляется в виде конечной популяции особей. Каждая особь в популяции обладает мерой приспособленности к окружающей среде. Процесс поиска оптимального решения описывается процессом моделируемой "эволюции", целью которой является нахождение особи (или множества особей), имеющей максимальную приспособленность, т.е. особи, соответствующей оптимальному значению управляемых параметров.
Каждая особь представлена в виде набора некоторого числа генов (битовых строк заданной длины) называемого хромосомой. Число генов в хромосоме соответствует размерности решаемой задачи; каждый ген используется для кодирования небольшого интервала значений одного из управляемых параметров проектируемой системы. По существу, такая кодировка соответствует разбиению пространства параметров на гиперкубы, которым соответствуют уникальные комбинации битов в хромосоме (генотип).
Для установления соответствия между гиперкубами разбиения области и бинарными строками, описывающими номера таких гиперкубов, использовался рефлексивный код Грея.
При взаимодействии особи с внешней средой ее генотип порождает внешне наблюдаемые количественные признаки: фенотип и оценку приспособленности. Фенотип особи определяется как точка, принадлежащая гиперкубу пространства поиска соответствующего генотипа. В рассматриваемом алгоритме применялся равномерный закон распределения точек фенотипа в соответствующем гиперкубе. (Более подробно предлагаемая символьнаямодель представлена в [6]).
Важно отметить, что в этом и состоит основное отличие предлагаемого способа формирования фенотипа от традиционного (см. [1,2]). Символьная модель, предлагаемых ранее генетических алгоритмов, предусматривала дискретизацию пространства параметров с шагом, соответствующим требуемой точности. При этом фенотип определялся как узел такой пространственной решетки, так что между генотипом и фенотипом особи существовало взаимно однозначное соответствие. Предлагаемая же нами модель не предусматривает однозначности, поскольку каждому генотипу может соответствовать целое множество фенотипов (что, вообще говоря, имеет место в природе). Это позволяет использовать более крупное разбиение пространства параметров, делая при этом длину хромосомного набора короче.
Для поиска оптимального разбиения пространства параметров на гиперкубы, кодируемые хромосомными наборами соответствующей длины NL (N — размерность задачи, L — длина кодировки одного гена), проводились испытания на четырех тестовых функция: De Jong 2, De Jong 3, De Jong 5 и функция Griewank'а. В качестве рассматриваемых вариантов были выбраны L1=4, L2=6, L3=8, L4=16. Эффективность поиска определялась по отношению к среднему (усредн. по 50 запускам) значению приспособленности популяции к максимальному значению после 1000 вычислений функции, что соответствует порядка 23-25 поколениям, при численности популяции 50 и формировании 20 брачных пар на каждом поколении, вероятность мутации была около 0.001. Результаты эксперимента приведены на рисунке 1.
Как видно из представленной диаграммы уже после L2=6 для представленных функций не происходит значительного улучшения эффективности поиска. Вообще, длина кодировки в значительной мере сказывается на функциях, ландшафту которых присущи скачкообразные изменения, как например у De Jong 3 или 5, и наоборот непрерывная функция De Jong 2, а тем более функция Griewank'а, слабо чувствительны к длине кодировки. Очевидно, такая особенность объясняется разбросом значений приспособленностей особей, имеющих одинаковые генотипы, этот разброс тем больше, чем крупнее гиперкубы разбиения пространства. Поэтому в процессе поиска для таких функций сложнее определить хромосомные наборы, которые бы соответствовали оптимальному решению.
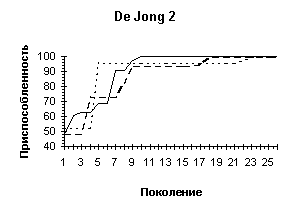
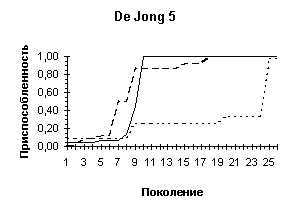
Однако, увеличение длины кодировки ускоряет процесс сходимости всех членов популяции к лучшему найденному решению (см. рисунок 3). Зачастую такой эффект не желателен, поскольку при этом большая часть пространства поиска остается неисследованной — преждевременная сходимость может не привести к оптимальному решению, кроме того, быстрая сходимость к одной области не гарантирует обнаружения нескольких равных экстремумов. Поэтому в вопросе выбора оптимальной длины кодировки нужно достичь некоторого компромиссного решения — с одной стороны L должно быть достаточно большим, чтобы все-таки обеспечить быстрый поиск, с другой стороны — по возможности малым, чтобы не допускать преждевременной сходимости и оставить алгоритму шанс отыскать несколько оптимальных значений. Мы предлагаем использовать хромосомные наборы длины 6N - 8N, где N — размерность задачи.
Формирование генотипов особей начальной популяции проводилось по принципу максимального побитого разнообразия (см. [6]). Максимальное побитовое разнообразие призвано обеспечить максимальное богатство генетического материала в начальной популяции.
Одной из особенностей предлагаемого ГА является отход от традиционной схемы "размножения", используемой в большинстве реализованных ГА [3] и повторяющих классическую схему, предложенную Голландом [1]. Классическая схема предполагает ограничение численности потомков путем использования так называемой вероятности кроссовера. Такая модель придает величине, соответствующей численности потомков, вообще говоря, недетерминированный характер. Мы предлагаем отойти от вероятности кроссовера и использовать фиксированное число брачных пар на каждом поколении, при этом каждая брачная пара "дает" двух потомков. Такой подход хорош тем, что делает процесс поиска более управляемым и предсказуемым в смысле вычислительных затрат.
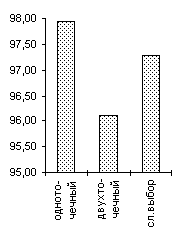
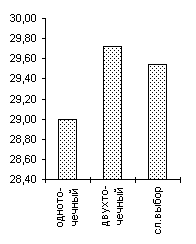
В качестве генетических операторов получения новых генотипов "потомков", используя генетическую информацию хромосомных наборов родителей мы применяли два типа кроссоверов — одно- и двухточечный. Вычислительные эксперименты показали, что даже для простых функций нельзя говорить о преимуществе того или иного оператора. Более того, было показано, что использование механизма случайного выбора одно- или двух точечного кроссовера для каждой конкретной брачной пары подчас оказывается более эффективным, чем детерминированный подход к выбору кроссоверов, поскольку достаточно трудно априорно определить который из двух операторов более подходит для каждого конкретного ландшафта приспособленности. Из диаграмм, представленных на рисунке 4 видно, что нельзя однозначно отдавать предпочтение одно- или двухточечному кроссоверу. Одноточечный оказался более эффективным на тестовых функциях De Jong'а 2 и 5, на двумерной функции Griewank'а и на двумерной функции Растригина, однако для функции De Jong'а 3, функции Griewank'а и Растригина от 10 переменных можно говорить о преимуществе выбора двухточечного оператора. Использование же случайного выбора преследовало целью прежде всего сгладить различия этих двух подходов и улучшить показатели среднего ожидаемого результата. Для всех представленных тестовых функций так и произошло, — случайный выбор оказался эффективнее худшего. Кроме того, в ряде случаев (функции Griewank'а, 10-мерная функция Растригина) применение случайного механизма в выборе кроссовера дало лучшие результаты по сравнению с детерминированными подходами.
Повышение эффективности поиска при использовании случайного выбора операторов кроссовера повлияло на то, чтобы применить аналогичный подход при реализации процесса мутагинеза новых особей, однако в этом случае преимущество перед детерминированным подходом не так очевидно в силу традиционно малой вероятности мутации (в наших экспериментах вероятность мутации составляла 0.001 - 0.01).
Как уже отмечалось, мы решили не использовать вероятность кроссовера в качестве одного из параметров алгоритма, ограничивая число воспроизводимых потомков фиксированным числом брачных пар. В связи с этим встал вопрос о том, каким образом из всего многообразия всех возможных пар выбрать лишь несколько. Предлагалось несколько подходов, однако мы рассмотрим здесь несколько показавшихся нам наиболее интересными.
Первый подход самый простой — это случайный выбор родительской пары ("панмиксия"), когда обе особи, которые составят родительскую пару, случайным образом выбираются из всей популяции, причем любая особь может стать членом нескольких пар. Несмотря на простоту, такой подход универсален для решения различных классов задач. Однако он достаточно критичен к численности популяции, поскольку эффективность алгоритма, реализующего такой подход, снижается с ростом численности популяции.
Второй способ выбора особей в родительскую пару — так называемый селективный. Его суть состоит в том, что "родителями" могут стать только те особи, значение приспособленности которых не меньше среднего значения приспособленности по популяции, при равной вероятности таких кандидатов составить брачную пару. Такой подход обеспечивает более быструю сходимость алгоритма. Однако из-за быстрой сходимости селективный выбор родительской пары не подходит тогда, когда ставиться задача определения нескольких экстремумов, поскольку для таких задач алгоритм, как правило, быстро сходится к одному из решений. Кроме того, для некоторого класса задач со сложным ландшафтом приспособленности быстрая сходимость может превратиться в преждевременную сходимость к квазиоптимальному решению. Этот недостаток может быть отчасти компенсирован использованием подходящего механизма отбора (о чем будет сказано ниже), который бы "тормозил" слишком быструю сходимость алгоритма.
Другие два способа формирования родительской пары, на которые хотелось бы обратить внимание, это инбридинг и аутбридинг. Оба эти метода построены на формировании пары на основе близкого и дальнего "родства" соответственно. Под "родством" здесь понимается расстояние между членами популяции как в смысле геометрического расстояния особей в пространстве параметров (для фенотипов), так и в смысле хэмминингого расстояния между хромосомными наборами особей (для генотипов). В связи с этим будем различать генотипный и фенотипный (или географический) инбридинг и аутбридинг. Под инбридингом понимается такой метод, когда первый член пары выбирается случайно, а вторым с большей вероятностью будет максимально близкая к нему особь. Аутбридинг же, наоборот, формирует брачные пары из максимально далеких особей. Использование генетических инбридинга и аутбридинга оказалось более эффективным по сравнению с географическим для всех тестовых функций при различных параметрах алгоритма. Наиболее полезно применение обоих представленных методов для многоэкстремальных задач. Однако два этих способа по-разному влияют на поведение ГА. Так инбридинг можно охарактеризовать свойством концентрации поиска в локальных узлах, что фактически приводит к разбиению популяции на отдельные локальные группы вокруг подозрительных на экстремум участков ландшафта, а аутбридинг как раз направлен на предупреждение сходимости алгоритма к уже найденным решениям, заставляя алгоритм просматривать новые, неисследованные области.
Обсуждение вопроса о влиянии метода создания родительских пар на поведение ГА невозможно вести в отрыве от реализуемого механизма отбора при формировании нового поколения. Сразу же отметим, что метод пропорционального отбора, как и другие методы, основанные на включение особи в новую популяцию по вероятностному принципу, давали настолько плохие результаты, что здесь даже не рассматриваются. В своих экспериментах мы использовали другие механизмы отбора, из которых выделим два: элитный и отбор с вытеснением.
Идея элитного отбора, в общем, не нова, этот метод основан на построении новой популяции только из лучших особей репродукционной группы, объединяющей в себе родителей, их потомков и мутантов. В литературе, посвященной ГА, например в [3], элитному отбору отводят место как достаточно слабому с точки зрения эффективности поиска. В основном это объясняют потенциальной опасностью преждевременной сходимости, отдавая предпочтение пропорциональному отбору. Однако наш опыт говорит о напрасности таких опасений. Быстрая сходимость, обеспечиваемая элитным отбором, может быть, когда это необходимо, с успехом компенсирована подходящим методом выбора родительских пар, например аутбридингом. Как видно из результатов, приведенных в таблице 1, именно такая комбинация "аутбридинг–элитный отбор" является одной из наиболее эффективных для рассматриваемых тестовых функций.
Второй метод, на котором хотелось бы остановиться, это отбор вытеснением. Отбор, построенный на таком принципе, носит бикритериальный характер — то, будет ли особь из репродукционной группы заноситься в популяцию нового поколения, определяется не только величиной ее приспособленности, но и тем, есть ли уже в формируемой популяции следующего поколения особь с аналогичным хромосомным набором. Из всех особей с одинаковыми генотипами предпочтение сначала, конечно же, отдается тем, чья приспособленность выше. Таким образом, достигаются две цели: во-первых, не теряются лучшие найденные решения, обладающие различными хромосомными наборами, а во-вторых, в популяции постоянно поддерживается достаточное генетическое разнообразие. Вытеснение в данном случае формирует новую популяцию скорее из далеко расположенных особей, вместо особей, группирующихся около текущего найденного решения. Этот метод особенно хорошо себя показал при решении многоэкстремальных задач, при этом помимо определения глобальных экстремумов появляется возможность выделить и те локальные максимумы, значения которых близки к глобальным.
Представленный алгоритм обладает достаточно широкими возможностями, — настроив соответствующим образом параметры системы, можно управлять процессом поиска в зависимости от поставленной задачи. Как уже отмечалось, существует, по крайней мере, три класса задач, которые могут быть решены представленным алгоритмом:
Основное различие в методах решения этих трех задач лежит в реализации различных уровней соотношения, которое в теории генетических алгоритмов называется как соотношение "исследование–использование".
Быстрый поиск одного экстремума, как правило, достигается использованием параметров, которые способствуют максимально быстрой сходимости за счет манипулирования только особями, обладающими лучшей приспособленностью, при этом более "слабые" члены популяции не участвуют в формировании родительских пар и не выживают после процедуры отбора. Этого можно достичь путем применения селективного выбора пар и элитного метода отбора. Понятно, что больший акцент в паре "исследование–использование" при этом делается именно на "использование".
Для решения второй задачи, очевидно, вопросу "исследования" пространства поиска должно уделяться гораздо большее внимание. Оно достигается за счет другого сочетания параметров и достаточно большой численности популяции, при этом ГА сможет выделить несколько (или даже все) глобальные экстремумы. В качестве примера решения такой задачи приведем экспериментальные данные, полученные при поиске максимумов двумерной функции Растригина. Параметры генетического алгоритма, использовавшиеся для максимизации этой функции, такие же, как и для решения других тестовых задач (см. комментарий к таблице 1.) Итак, средние показатели процесса поиска по 50 испытаниям, в скобках для сравнения приведены результаты, опубликованные в [6]:
Для выделения нескольких глобальных максимумов, лучше использовать такую комбинацию: аутбридинг в сочетании с инбридингом, в качестве естественного отбора достаточно использовать элитный отбор или отбор с вытеснение (последний более надежный). Максимальная эффективность поиска достигается в сочетании аутбридинга и инбридинга, причем аутбридинг рекомендуется использовать в начале поиска, достигая максимально широкого "исследовании", а завершать поиск лучше уточнением решения в локальных группах, используя инбридинг.
И наконец третья задача. Особенность ее решения состоит в том, что при достаточно большом размере популяции и небольшом заданном количестве брачных пар проявляется интересное свойство поведения генетического алгоритма: в процессе поиска проявляются черты рельефа ландшафта функции приспособленности (овраги, холмы, долины). На рисунке 5 видно, что оставляя области, которым соответствуют меньшая приспособленность, ГА группирует особи ближе к вершинам холмов, в область притяжения которых они попали. Это эквивалентно определению локальных экстремумов, значения которых близки к оптимальным. Продолжение поиска ведет к тому, что особи, сгруппировавшиеся вокруг локальных экстремумов, постепенно "вымирают", а их место в популяции начинают занимать особи с лучшей приспособленностью близкие к глобальным максимумам. Использование же отбора с вытеснение в какой-то мере может препятствовать этому процессу, давая шанс "выжить" особям около локальных экстремумов.
, -1.28<=x1,2<=1.28. F*=F(1.00, 1.00) = 100.00
, -5.12<=x1,2,3,4,5<=5.12. F*=30 на гиперплоскости 5.00<=x1,2,3,4,5<=5.12
, где a1j=16[(j mod 5)-2], a2j=16[(j % 5)-2].
F*=F(-16,-32)=1.002 при
, -5.12<=x1,2<=5.12.
F*=F(4.52299, 4.52299)=F(-4.52299, 4.52299)=F(-4.52299, -4.52299)=F(4.52299, -4.52299)=80.7065
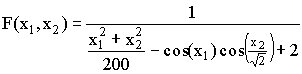, -20.0<=x1,2<=20.0. F*=F(0.00, 0.00)=1.0
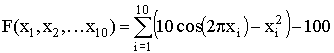. F*=F(0.00, 0.00:0.00)=0.00 при -5.12<=x1,2,…,10<=5.12
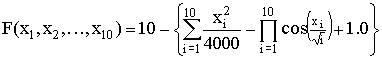, -5.12<=x1,2,…,10<=5.12. F*=F(0.00, 0.00:0.00)=10.00
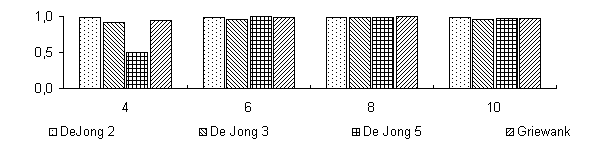
Отношение найденного максимального значения к реальному максимуму при различной длине кодировки гена для 4 тестовых функций.
 |
 |
 |
 |
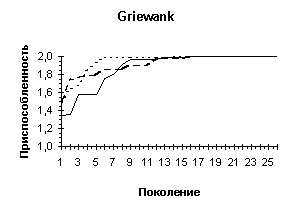На рисунке представлены графики изменения приспособленности лучшей особи в популяции при различной длине кодировки (непрерывная линия — L = 10, разрывная — L = 6, пунктирная —— L = 4).
| De Jong 2 (L=4) |  |
| De Jong 2 (L=10) |  |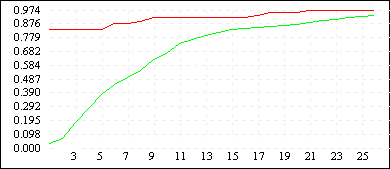
| De Jong 5 (L=4) |  |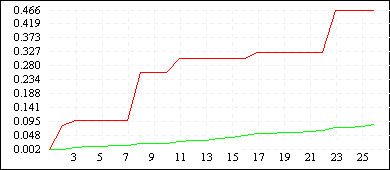
| De Jong 5 (L=10) |  |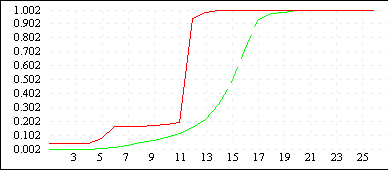
На диаграммах представлены изменение лучшей, средней и худшей приспособленностей особей в популяции. Нетрудно видеть, что увеличение длины хромосомного набора не столько ускоряет процесс поиска наилучшего значения приспособленности, сколько влияет на улучшение приспособленностей наихудших особей в популяции, что приводит к более быстрой сходимости алгоритма в ущерб исследованию пространства поиска.
| De Jong 2 | De Jong 3 | Griewank (n=10) |
 |
 |
 |
Эффективность ГА при использовании различных операторов кроссовера. На диаграммах представлены результаты, усредненные по 50 запускам (каждый запуск — около 5000 вычислений для 10-мерных функций или 1000 для остальных).
| De Jong 2 | De Jong 5 | ||
| Быстрый поиск | Описание ландшафта | Быстрый поиск | Описание ландшафта |
 |
 |
 |
 |
| Griewank n=2 | Растригин n=2 | ||
| Быстрый поиск | Описание ландшафта | Быстрый поиск | Описание ландшафта |
 |
 |
 |
 |
На рисунке представлены популяции особей в пространстве поиска для тестовых функций на 25-ом поколении генетического алгоритма при параметрах, настроенных на быстрый поиск одного максимума и для задачи описания ландшафта.
| панм-элит | панм-выт | селек-элит | селект-выт | инбр-элит | инбр-выт | аутбр-элит | аутбр-выт | |
| De Jong 2 | ||||||||
| Макс | 99,999 | 99,964 | 99,998 | 99,982 | 99,999 | 99,983 | 99,986 | 99,980 |
| Мин | 92,254 | 90,735 | 83,529 | 80,211 | 83,725 | 88,445 | 91,754 | 94,843 |
| Cр.знач | 98,038 | 98,666 | 96,595 | 96,903 | 98,464 | 98,833 | 98,811 | 98,639 |
| De Jong 3 | ||||||||
| Макс | 29,000 | 29,000 | 30,000 | 30,000 | 28,000 | 29,000 | 30,000 | 30,000 |
| Мин | 27,000 | 27,000 | 27,000 | 29,000 | 24,000 | 25,000 | 28,000 | 28,000 |
| Cр.знач | 28,320 | 28,160 | 29,280 | 29,180 | 26,880 | 27,180 | 28,780 | 28,620 |
| De Jong 5 | ||||||||
| Макс | 1,002 | 1,002 | 1,002 | 1,002 | 1,002 | 1,002 | 1,002 | 1,002 |
| Мин | 0,502 | 0,550 | 0,202 | 0,966 | 0,202 | 0,715 | 0,988 | 0,910 |
| Ср.знач | 0,982 | 0,981 | 0,985 | 1,000 | 0,962 | 0,978 | 1,001 | 0,991 |
| Griewank n=2 | ||||||||
| Макс | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 |
| Мин | 0,836 | 0,871 | 0,871 | 0,871 | 0,871 | 0,869 | 0,872 | 0,906 |
| Ср.знач | 0,963 | 0,977 | 0,953 | 0,960 | 0,946 | 0,970 | 0,993 | 0,988 |
| Растригин n=10 | ||||||||
| Макс | ||||||||
| Мин | ||||||||
| Ср.знач | ||||||||
| Griewank n=10 | ||||||||
| Макс | 9,356 | 9,479 | 9,476 | 9,396 | 9,260 | 9,255 | 9,586 | 9,467 |
| Мин | 9,027 | 9,034 | 9,051 | 9,078 | 8,708 | 8,445 | 9,069 | 9,069 |
| Ср.знач | 9,158 | 9,173 | 9,198 | 9,203 | 8,936 | 8,912 | 9,235 | 9,212 |
В таблице приведены результаты поиска по 50 запускам при различных параметрах генетического алгоритма. Для всех примеров: L=6, численность популяции 50, число брачных пар 20, вероятность мутации 0.01. Число вычислений функции: для первых четырех около1000, для двух последних около 5000.
Исаев Сергей.
http://www.i2.com.ua/