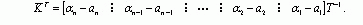8. Синтез модального регулятора на основе желаемого расположения полюсов замкнутой динамической системы.
8.1 Синтез модального регулятора непрерывной динамической системы на основе преобразования уравнения состояния к КФУ.

Решение этого уравнения будет иметь вид:

Определим матрицу преобразования Т [7]:

где QD – матрица управляемости (достижимости)
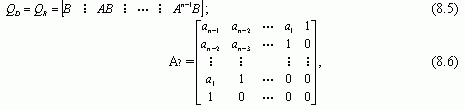
где аi – коэффициенты характеристического полинома

Определим новый вектор состояния `хR по формуле

Подставляя выражение (8.7) в (8.1), получим
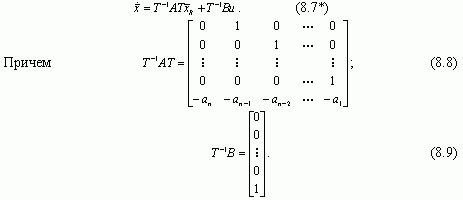
Далее выберем множество желаемых собственных значений m1, m2,…, mn. Желаемое характеристическое уравнение запишется [3,8]
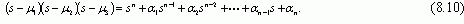
Запишем произведение матриц и Т по столбцам
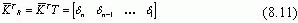
Когда используется управляющее воздействие 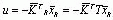 для управления системой (8.7*), уравнение состояния преобразовывается к виду
для управления системой (8.7*), уравнение состояния преобразовывается к виду

Характеристическое уравнение

Это характеристическое уравнение такое же, как и характеристическое уравнение для обычной (не преобразованной) системы, определяемой уравнением (8.1), когда u=-` `х. Это может быть показано следующим образом:
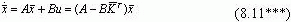
Характеристическое уравнение для этой системы
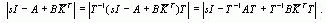
Теперь упростим характеристическое уравнение системы в канонической форме управляемости. Что касается уравнений (8.8), (8.9) и (8.11), мы получим

Это характеристическое уравнение для системы с обратной связью по состоянию. Следовательно, оно должно быть равно уравнению (8.10), т.е. желаемому характеристическому уравнению. Приравнивая коэффициенты при одинаковых степенях S, мы получаем систему уравнений

Решая предшествующую систему уравнений (8.12*) для di и заменяя их в уравнении (8.11) мы получим
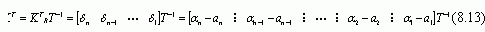
Таким образом, если система вполне управляема, все собственные значения могут быть помещены в желаемой области с помощью выбора матрицы согласно уравнению (8.13).
Основываясь на выше приведенных преобразованиях для матриц К, предлагается следующий алгоритм синтеза модального регулятора.
- Шаг 1: Проверка матрицы управляемости. Ранг матрицы управляемости должен быть равен n. Иначе уравнение (8.13) не может быть использовано.
- Шаг 2: Из характеристического полинома для матрицы А
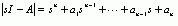
определяют значения а1, а2, …,аn.
- Шаг 3: Определяют матрицу преобразования Т, которая преобразовывает уравнение состояния системы в КФУ. (Если данное уравнение системы уже записано в КФУ, то полагают Т=I). Отметим, что нет необходимости записывать уравнения состояния в КФУ. Все, что нам нужно – найти матрицу преобразования Т. Матрица преобразования Т определяется уравнением (8.4), или Т=QR*A, где QR определяется уравнение (8.5), а A - выражением (8.6).
- Шаг 4: Используя желаемые собственные значения (желаемые полюса замкнутой системы), записывают желаемый характеристический полином:

и определяют затем коэффициенты 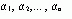 характеристического полинома замкнутой системы.
характеристического полинома замкнутой системы.
- Шаг 5: Искомая матрица обратной связи по состоянию может быть определена из следующего уравнения
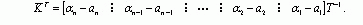



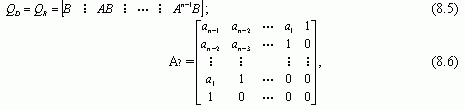


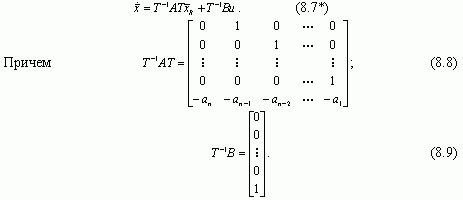
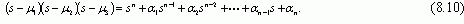
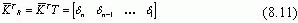
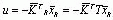 для управления системой (8.7*), уравнение состояния преобразовывается к виду
для управления системой (8.7*), уравнение состояния преобразовывается к виду


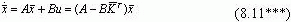
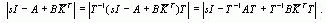


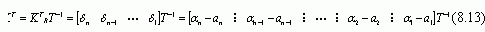
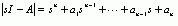

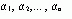 характеристического полинома замкнутой системы.
характеристического полинома замкнутой системы.