Граничный модуль односвязной области с гладкой жордановой границей

Лебедева И.А., Степанов Т.Л.

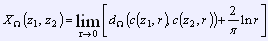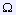Граничный модуль:, где - односвязная область, границей которой является гладкая жорданова кривая, 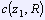, 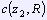- окружности радиуса R с центрами в точках z₁ и z₂, - экстремальная длина семейства локально-спрямляемых кривых, лежащих в 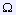и соединяющих 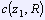и 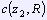(см. рис. 1).

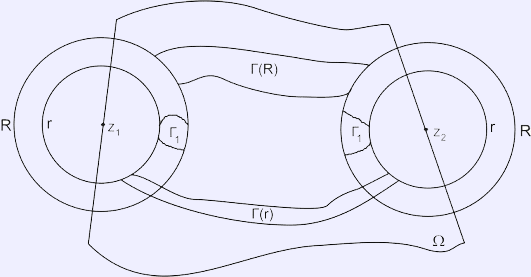
Рисунок 1.

Нами исследованы следующие свойства граничного модуля:

Свойство 1. Пусть даны две функции и 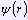, принимающие только положительные вещественные значения, и такие, что 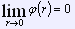и 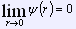. Тогда, если существует , то имеет место равенство:

Свойство 2. Пусть конформно и однолистно отображает односвязную область 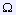с гладкой жордановой границей на область с гладкой жордановой границей. Тогда:

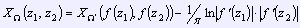
На основании полученных свойств мы сумели вычислить граничный модуль единичного круга: 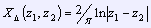, где .

Теорема об искажении хорд. Пусть функция 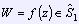и осуществляет конформное и однолистное отображение на область K с гладкой жордановой границей, лежащую в единичном круге. Точки и 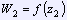принадлежат как границе области K, так и единичной окружности. Тогда:

Равенство достигается при любом отображении единичного круга на себя.

Рисунок 2.

Литература.

1. Альфорс Л. Лекции по квазиконформным отображениям. Перевод с английского. – М.: «Мир». – 1969. – 132 с.
2. Голузин Г.М. Геометрическая теория функций комплексного переменного. – М.: «Наука». – 1966. – 626 с.
3. Дженкинс Дж. Однолистные функции и конформные отображения. Перевод с английского. – М.: издательство Иностранной литературы. – 1962. – 265 с.

Полная версия статьи напечатана в сборнике работ по результатам конференции "Проблеми науки та освіти", секция: Фундаментальные исследования в области математики, физики, химии.