Численные методы поиска оптиума функции с ограничениями
Математическая постановка задачи.
Общая задача нелинейного программирования:
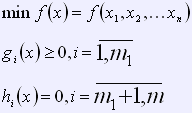
Данная задача решается множеством итерационных способов, общим для которых есть то, что одним из определяющих факторов для направления движения из предыдущей точки является градиент функции.
Описание метода штрафных функций для решения общей задачи нелинейного программирования.
Для решения задачи нелинейного программирования применяются самые разнообразные методы, среди которых метод штрафных функций удобен тем, что состоит лишь в построении самой штрафной функции, учитывающей ограничения, а уже её оптимум будет решением общей задачи. Для внешней точки выгодно использовать метод внешней точки, а для внутренней наилучшую сходимость даёт комбинированный метод.
Штрафная функция для метода внешней точки:

Штрафная функция для комбинированного метода:
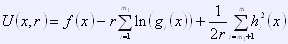
Алгоритм метода штрафных функций.
- Строим штрафную функцию и выбираем начальную точку и произвольный коэффициент штрафа.
- С помощью любого метода безусловной оптимизации находим экстремум функции x1(r1). Начиная с точки x1(r1) с помощью метода безусловной оптимизации ищем экстремум функции U(x,r2), где r1>r2>0.
- Описанную процедуру продолжаем до тех пор, пока |U(x,rk+1)-U(x,rk)|<eps.
Метод бузусловной оптимизации - алгоритм Пирсона.
Алгоритм Пирсона относится к группе методов переменной метрики. Эти методы называют ещё квазиньютоновскими или градиентными с большим шагом. Они аппроксимируют матрицу Гессе или обратную к ей, но используют для этого только первые производные. В большинстве из методов применяются сопряжённые направления.
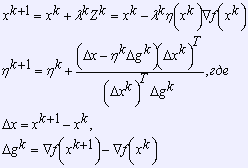
К методам переменной метрики относятся также метод Дэвидона-Флетчера-Пауэла и проективный алгоритм Ньютона-Рафсона.

Рисунок 1 - Пример оптимизации функции y=(x2-x12)2 +(1-x12)2 без ограничесний методом Пирсона.

Рисунок 2 - Пример оптимизации функции y=2*x1+4*x2-x12-x22 с ограничениями методом штрафных функций.
Литература.
- Шенен П., Коснар М. Математика и САПР. –М: Мир, 1988.
masters donntu