Сиренко А.И., Волощук Л.А.

Одесская государственная академия холода

Определение параметров потока запросов к WEB серверу

 

При проектировании компьютерных сетей важнейшими характеристиками, которые должны быть известны к началу проектирования, являются требования к характеристикам трафика, который будет передаваться по сети.

Теоретические методы проектирования сетей требуют  знания типа распределения входящего потока заявок, распределения времени обслуживания заявок, моментов распределения [1].  Особый интерес представляют моменты 1-го (среднее значение) и 2-го (среднеквадратичное отклонение) порядков, как обобщающие значения.

Ввиду широкого распространения сети Internet и протокола HTTP, возрастает число процессов, работающих по этому протоколу  и требующих для своего функционирования использования WEB-сервера. Разработанные модели работы WEB-сервера [2] так же предполагают, что приходящий трафик имеет определенные типы распределения заявок.

Таким образом, знание характеристик трафика является актуальной задачей при выборе математического аппарата для проектирования сетей и использования в проектировании наработанных моделей.

Задачи, стоящие в исследовании

1)     Построить графики распределения задержек между поступающими запросами.

2)     Проверить с помощью критерия А.Н. Колмогорова гипотезу о том, что распределение задержек между поступлением запросов входящего HTTP трафика, подчиняются нормальному распределению при уровне значимости a =0.1

Для решения задач исследования была разработана методика, в основу которой  взяты положения, опубликованные в [3]. В общем случае для решения задачи можно предложить следующие этапы.

1)     Произвести первичный анализ лог-файлов веб-сервера. На основе этого анализа выбирается промежуток времени для дальнейшей обработки, а так же переход от вида представления времени. Изначально в лог-файле фиксируется время поступления запроса, из этих данных необходимо составить последовательность промежутков времени между поступлениями запросов.

2)     По результатам наблюдений построить вариационный ряд, в котором значения отсортированы по возрастанию,  сгруппировать результаты по интервалам (построить статистический ряд). Группировка по интервалам удобна, когда количество наблюдений велико.

3)     На основе статистического ряда построить гистограмму и график эмпирической функции распределения интервалов между заявками.

4)     Вычисление моментов (математического ожидания и дисперсии) распределения задержек между запросами.

5)     Проверка гипотез о распределении задержек между запросами по нормальному закону с помощью критерия А.Н. Колмогорова.

 

Для демонстрации практического применения методики были взяты данные о запросах на сервер www.uo.od.ua

1)     В связи с тем, что характер трафика в дневное время отличается от ночного времени, для исследования был взят промежуток между 9.00 и 22.00 часами. Для дальнейших расчетов были просчитаны задержки между соседними запросами

2)     За исследуемое время поступило n=1529 запросов. В результате измерений оказалось, что минимальное значение задержки равно 0 (задержка между соседними запросами меньше 1 секунды), максимальная задержка равна 298 секунде. Для построения гистограммы целесообразно произвести разбиение результатов на интервалы. Количество интервалов  возьмем из соотношения Стерджесса: 

y =1,441*ln(n)+1                       (1)

где n – число измерений задержек между запросами

Длины интервалов выберем по формуле:

                      (2)

где  – максимальное и  – минимальное значения промежутков времени между запросами, y – количество интервалов.

Таким образом, округляя значения, полученные в (1) и (2), получаем число интервалов y=12, длина интервала h=25. Результаты построения статистического ряда приведены в табл.1

i

Xi

Ni

Ni/n

i

Xi

Ni

Ni/n

1

0

959

0,6279

7

150

10

0,0065

2

25

244

0,1589

8

175

11

0,0072

3

50

135

0,0883

9

200

10

0,0065

4

75

88

0,0576

10

225

4

0,0026

5

100

39

0,0255

11

250

0

0,0000

6

125

27

0,0177

12

275

2

0,0013

 

Где i – номер интервала; Xi – начальное значение границы интервала; Ni – количество значений переменной, попавших в интервал (частота);  Ni/n – отношение частоты к объему выборки (относительная частота).

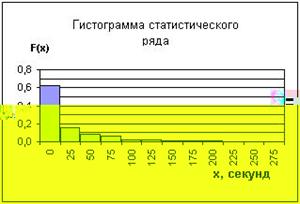
3)  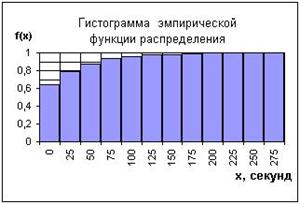   На основе данных по всему объему выборки  построим гистограмму и график эмпирической функции распределения временных интервалов.

                       Рис. 1                                                 Рис. 2

На рис.1 изображена эмпирическая функция распределения, показывающая вероятность того, что любое произвольное число X из выборки меньше значения x.

На рис.2 изображена гистограмма распределения, показывающая вероятность того, что любое произвольное число X из выборки равно значению x.

4)     В результате вычислений получены значения математического ожидания  M(x)= 30.6, дисперсии D(x)= 1822.33

5)     Для применения критерия А.Н. Колмогорова данные измерений требуется представить в виде вариационного ряда. В качестве меры расхождения между теоретической и эмпирической  функциями распределения непрерывной случайной величины Х используется модуль максимальной разности теоретической и эмпирической  функциями для каждого из значений, представленных в измерениях.

В результате вычислений  максимальное расхождение составило

=max(0.492647; 0.493301) =  0.493301

Критическое значение расхождения

Где a уровень значимости a =0.1;  – табличная величина, зависящая от уровня значимости; n – количество измерений

Поскольку величина  больше критического значения (), гипотеза о принадлежности выборки нормальному закону отвергается.

 

Методика, предложенная в данной работе, позволяет получать информацию о характеристиках, а так же делать предположения о виде распределения временных промежутков HTTP трафика. Эта информация может быть использована при анализе нагрузки на WEB- сервер, повышения эффективности использования аппаратных ресурсов.

Так как WEB-сервера активно используются в процессе функционирования компьютерных сетей, то результаты предложенной методики могут быть использованы в процессе моделирования работы корпоративных сетей.

 

 

Литература

1. В.М.Вишневский “Теоретические основы проектирования компьютерных сетей”

2. Mikael Andersson, Jianhua Cao, Maria Kihl and Christian Nyberg “Performance Modeling of an Apache Web Server with Bursty Arrival Traffic”

3. Ходасевич Г.Б. “ОБРАБОТКА ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ НА ЭВМ”  СПб.: СПбГУТ, 2002.

 

e-mail: avatara@odessa.net

e-mail: lav@eurocom.od.ua

 

Источник: http://www.rusnauka.com/Article/PC/9.html