| Автобиография | Магистерская работа | Библиотека |
| Ссылки | Индивидуальное задание | Отчет о поиске |

|
Ткаченко Александр Валерьевич
Разработка нейросетевой системы управления котлом энергоблока |
|
ДЛЯ ОБУЧЕНИЯ В СИСТЕМАХ РЕАЛЬНОГО ВРЕМЕНИ
Скобцов Ю. А., Ткаченко А. В. Abstract. Skobtsov Y.A., Tkachenko A.V. Program realization of neural networks for learning in real-time systems. Problem of program realization of artificial neural networks for real-time system is considered. Best methods for neural network training are overviewed. Resilient backpropagation algorithm is considered as one of the most efficient weight adaptation method. Application of con-jugate graph for gradient generation is shown. Problem of weight initialization is considered and Ngueyn-Widrow method is applied to give good first approximation. Program library implementing overviewed methods is developed on C. High speed of the library is shown in comparison with Mathlab.
Анализ исследований по рассматриваемой проблеме. Существуют два способа реализации искусственных нейронных сетей – аппаратная и программная. Программная реализация, уступая аппаратной по скорости работы и автономности, обладает рядом очевидных преимуществ, связанных с простотой использования и внедрения в информационно-управляющую систему.
Постановка задачи и цели исследований. Цель данного исследования – разработка библиотеки программ, сокращенно называемой OSNN (On-Line System Neural Network), позволяющей моделировать и обучать многослойные нейронные сети прямого распространения в системах реального времени. В качестве языка программирования используется широко известный и легко переносимый на другие платформы язык С++. Для организации обучения будут использоваться методы признанные в настоящее время наиболее эффективными. Под эффективностью алгоритма будем понимать в первую очередь время работы алгоритма, а во вторую объем требуемых ресурсов. В тоже время при одинаковой эффективности предпочтение будет отдаваться алгоритмам более простым в реализации. В качестве возможных функций активации сети будет рассматриваться линейная функция f(u)=u и гиперболический тангенс f(u)=(eu-e-u)/(eu+e-u).
Задача обучения нейронной сети. Задано множество пар векторов {x,d} называемое обучающим множеством
, где {x} входной вектор, а {d} желаемый выходной вектор. {y} - множество реакций нейронной сети на вход {x}. Тогда мера разницы между {y} и {d}
(E=|| y - d ||) называется ошибкой обучения. Используя среднюю квадратичную меру ошибки получим
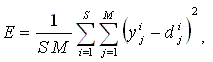 (1)
(1)
где S – число обучающих пар, M - размерность выходного вектора.
Метод “неунывающего” обратного распространения RPROP. Лучшим из эвристических алгоритмов обучения является алгоритм RPROP (resilient backpropagation) [2]. Его основным преимуществом над методами сопряженных градиентов является простота реализации при высокой скорости сходимости и низких требованиях к погрешности вычисления градиента. Алгоритм RPROP основывается на поведении знаков градиентов. Он не требует сложных вычислений и не зависит от величин производных. Приращение на каждом шаге вычисляется индивидуально для каждого веса. Приращение вычисляется по формуле 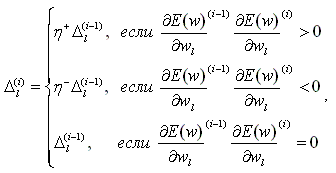 (2) (2)
где 0 < η- (=0.5) < 1 < η+ (=1.2)
Величина приращения усиливается фактором η+ в том случае, когда алгоритм сходится к минимуму и производная не меняет знак. Это ускоряет процесс на плоских участках и замедляет поиск, в случае пропуска локального минимума.
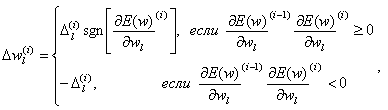 (3) (3)
где sgn[*] – функция знака. Когда производная ошибки изменяет знак, показывая, что минимум пропущен, происходит возврат к предыдущему значению веса
wl(i-1)
. При этом, для того что бы избежать изменения знака и на следующем шаге необходимо обнулить значение производной
Метод потоковых графов для генерации градиента. Важным и трудоёмким этапом обучения является нахождения градиента целевой функции. Формулы расчета градиента, взятые в явном виде от целевой функции очень сложны и неудобны для практического применения, особенно в том случае если сеть содержит больше одного скрытого слоя. Поэтому представляется удобным на основе метода потоковых графов построить простые правила формирования компонентов градиента, которые имеют постоянную структуру, не зависящую от сложности сети [4].
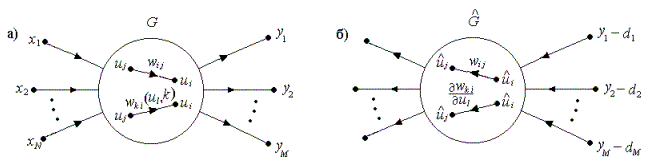
Рисунок 1 - Иллюстрация применения способа формирования и возбуждения сопряженного графа: а) исходный граф G ; б) сопряженный граф 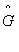 . .

Рисунок 2 - Сопряженные графы для генерации вектора градиента однонаправленной многослойной сети: а) выходной граф сети б) сопряженный граф сети. Теперь можно рассчитать любой компонент вектора градиента ошибки. Для линейной дуги графа, описываемой весом wij, формула имеет вид: 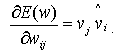 (4)
(4)
Для нелинейной дуги графа G , описываемой функцией wkl (vl ,K) , получаем  (5)
(5)
Представленные выражения применимы для любых систем (линейных, нелинейных, рекуррентных и т.п.). Рассмотрим изображенною на рис. 2а типовую многослойную сеть (состоящую их m слоев) с произвольной непрерывной функцией активации нейронов. Количество нейронов в каждом слое обозначим
Kj (j=1, 2, …m), причем последний слой является выходным слоем сети, содержащим
Kj=M
нейронов. Выходные сигналы нейронов в конкретных слоях обозначим vj(k).
. На рис. 2б представлен сопряженный граф. Сопряженный граф возбуждается разностями между фактическими yi
и ожидаемыми значениями di . Нелинейные дуги графа G заменяются в сопряженном графе  (6)
(6)
Применение формулы (6) реализовано в OSNN и позволяет уменьшить время вычислений производной в несколько раз.
Сформулированное правило и приведенные формулы являются чрезвычайно простыми и удобными для программной реализации.
Метод инициализации весов Нгуена-Видроу.
Начальная инициализация весов ней-ронной сети имеет огромное влияние на количество итераций обучения. В самом простом случае начальные значения весов выбираются случайно из некоторого промежутка. Нгуен и Видроу [3] предложили метод, позволяющий значительно сократить количество итераций обучения за счет большей близости начальных значений к оптимальным. Идея метода в том, чтобы значения весов позволяли кусочно-линейно аппроксимировать входной сигнал при помощи линейных участков функции активации. Для сигмоидальной функции активации ли-нейная область расположена на интервале аргумента (-1,1). Следовательно, для случая слоя с одним входом и H выходами необходимо чтобы выполнялось условие
где x – равномерно распределенная величина из интервала [xmin , xmax ]. Приняв ширину интервала для вех нейронов одинаковой и в сумме заполняющей входной диапазон  (11)
(11)
получим значения весов смещения как равномерно распределенную величину на интервале 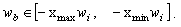 (12)
(12)
Аналогично получаем формулу для слоя с I входами и H выходами. При этом желательно слегка расширить интервалы “интереса” весов, оставив распределения весов смещения прежним.  (13)
(13)
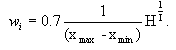 (14)
(14)
Соответственно веса смещения - равномерно распределенная величина на интервале  (15)
(15)
Тестирование. Проведем сравнительное тестирование разработанной библиотеки программ OSNN и Matlab Release 13. В Matlab в качестве тестируемых алгоритмов обучения взят алгоритм trainrp, реализующий алгоритм RPROP, и trainscg, реализующий метод масштабируемых сопряженных градиентов (SCG). В качестве алгоритма инициализации использована реализация метода Нгуена-Видроу - initnw. Тестирование производилось на компьютере с процессором Pentium4 2,4ГГц и 512Мб оперативной памяти под управлением операционной системы Windows XP. Библиотека OSNN откомпилирована компилятором C++ Builder6 с включенной оптимизацией скорости. В качестве обучающих множеств использовались 3 тестовых набора данных (benchmarks) различной сложности: Sin, Cancer, Building [6]. Краткие характеристики этих тестовых наборов приведены в таблице 1.
Тест Sin – небольшая задача аппроксимации периода функции синуса. Canser – задача средней размерности, представляет собой классификацию опухолей на злокачественные и доброкачественные. Building – задача большой размерности, представляющая собой модель расхода электроэнергии, горячей и холодной воды в здании в зависимости от внешних условий. Проведены 30 запусков обучения каждого из тестов. Результаты тестирования представлены в таблице 2. Таблица 2. Результаты тестирования OSNN и Mathlab.
Основным критерием сравнения программ, который интересует нас при разработки информационно-управляющих систем реального времени, является время обучения. Кроме того, сравнение OSNN и trainrp по количеству итераций позволяет определить лучшую реализацию алгоритма RPROP, в смысле выбора начальных значений и коэффициентов. Сравнение trainrp и trainscg позволит показать эффективность методов для задач различной размерности. На тестовом наборе SIN OSNN показала значительно лучшие результаты по всем характеристикам: общему времени обучения, времени одной итерации и их количеству. На задаче малой размерности заметно преимущество метода SCG, использующего вторые производные для более быстрой сходимости. В тесте Cancer время обучения всех программ приблизительно одинаково. Реализация метода RPROP в Mathlab показала результаты по количеству итераций лучше чем OSNN. Это можно объяснить отличной от OSNN реализацией алгоритма начальной инициализация сети, дающее более высокие результаты для слоев с малым количеством нейронов. В следующем тесте Building OSNN полностью оправдала свою разработку, сократив время обучения более чем в два раза, причем как за счет большей скорости вычислений, так и за счет изменений в реализации RPROP. В этом тесте, как на задаче большой размерности, RPROP наконец, показал свое значительное превосходство над методом SCG.
Выводы. Рассмотрена проблема программной реализации нейронных сетей в системах реального времени. Сделан вывод о необходимости разработки интегрируемой библиотеки программ, позволяющей моделировать и обучать нейронные сети прямого распространения. Рассмотрен алгоритм неунывающего обратного распространения и предложена его эффективная реализация. Изучен способ формирования градиента на основе метода потоковых графов. Рассмотрен алгоритм начальной инициализации весов Нгуена-Видроу. Разработана программная реализация описанных методов в виде библиотеки программ под названием OSNN. Проведено сравнительное тестирование OSNN с реализациями алгоритмов RPROP и SCG на Mathlab.
1. Осовский С. Нейронные сети для обработки информации: Пер. с польского. М: Финансы и статистика, 344 с., 2002.
Скобцов Ю. А., Ткаченко А. В. Программная реализация нейронных сетей для обучения в системах реального времени. // Наукові праці Донецького державного технічного університету. Сер. обчислювальна техніка та автоматизація, випуск 66. – Донецьк: ДонНТУ. – 2005. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
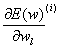 . Таким образом, алгоритм имеет вид:
. Таким образом, алгоритм имеет вид:
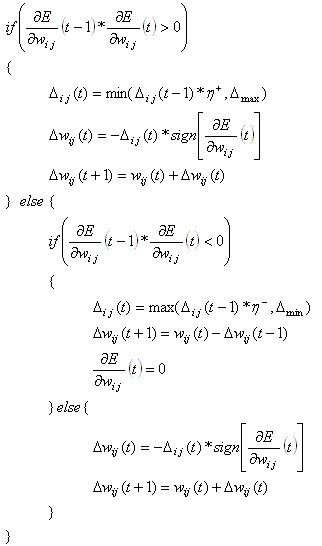

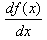 , значения которых рассчитываются в каждой точке x=ui . Если функция активации нейронов - гиперболический тангенс, то производная рассчитывается непосредственно на основе известной формулы через уже вычисленное значение f(x)
, значения которых рассчитываются в каждой точке x=ui . Если функция активации нейронов - гиперболический тангенс, то производная рассчитывается непосредственно на основе известной формулы через уже вычисленное значение f(x)
 (7)
(7)
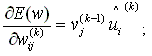 (8)
(8)
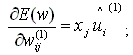 (9)
(9)