УДК 681.3
Скобелев В.Г.
Институт прикладной математики и механики НАН Украины, г. Донецк,
e-mail:
skbv@iamm.ac.donetsk.ua
Ткаченко А.В.
Донецкий национальный технический университет, г. Донецк,
e-mail: a.tkachenko@kiev-konti.com
avtkachenko@mail.ru
МНОГОПОЛЬЗОВАТЕЛЬСКИЙ ДОСТУП К КАНАЛУ СВЯЗИ НА ОСНОВЕ ЦИКЛИЧЕСКИХ АТТРАКТОРОВ
Skobelev V.G., Tkachenko A.V.
Multiple-access communications based on cyclic attractors
In the given paper it is proposed some scheme, intended to provide multiple access communications on the base of distribution between the clients some cyclic attractors of one-dimensional piece-wise linear mappings in the role of inherent channel’s alphabet. It is established that cyclic attractors’ presentation via symmetric group’s elements provides us with some non-stationary computationally secured channel’s shielding, intended to prevent external passive attacks.
Введение
Необходимость организации многопользовательского доступа к каналу связи привела к выработке двух основных подходов, основанных, соответственно, на распределении между пользователями времени доступа к каналу связи (стан-дарт типа TDMA) и частот в качестве внутреннего алфавита пользователя в кана-ле связи (стандарт типа FDMA). При этом ясно, что эффективное использование канала связи, ориентированное на пользователя и обеспечивающее некоторый уровень защиты передаваемой информации от пассивных внешних атак (кроме применения методов непосредственного шифрования и обычного физического экранирования канала), можно достичь только за счет решения многокритериаль-ной задачи, формулируемой в терминах комбинации указанных подходов.
Необходимость организации многопользовательского доступа к каналу связи привела к выработке двух основных подходов, основанных, соответственно, на распределении между пользователями времени доступа к каналу связи (стандарт типа TDMA) и частот в качестве внутреннего алфавита пользователя в канале связи (стандарт типа FDMA). При этом ясно, что эффективное использование канала связи, ориентированное на пользователя и обеспечивающее некоторый уровень защиты передаваемой информации от пассивных внешних атак (кроме применения методов непосредственного шифрования и обычного физического экранирования канала), можно достичь только за счет решения многокритериальной задачи, формулируемой в терминах комбинации указанных подходов.
Переход к цифровой связи естественно трансформировал распределение частот в распределение кодов между пользователями (стандарт типа CDMA). Соответственно изменилась и задача управления доступом пользователей к каналу связи. Более того, как формулировка, так и метод решения этой задачи существенно зависит от механизма генерации кодов и их распределения между пользователями. В [1-4] развит подход к генерации кодов, основанный на использовании свойств детерминированного хаоса динамических систем (рис. 1). Это направление теории систем, интенсивно разрабатываемое в течение последнего двадцатилетия, доказало свою способность успешно решать широкий класс задач обработки информации за счет отхода от классического принципа: усложнение поведения информационной системы влечет усложнение ее структуры (см., напр., [5-7]).
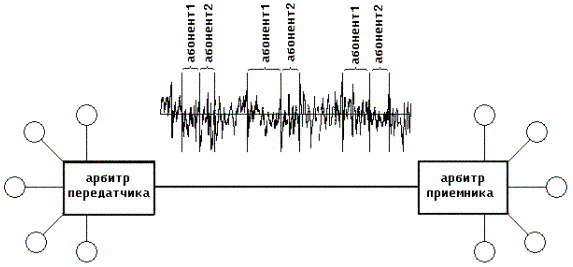 / /
Рисунок 1 - Передача информации по многопользовательскому каналу связи при помощи хаотического сигнала
Между подходами, предложенными в [1-3] и в [4] имеется следующее принципиальное различие.
В [1-3] хаотические сигналы применяется только в роли эффективного гибкого средства для формирования квази-шума и совершенно не уделяется внимания вопросам, связанным с исследованием многообразия хаотических режимов, гибким управлением их динамикой, самосинхронизацией и конфиденциальностью передаваемой информации.
В [4], напротив, на примере исследования свойств отображения Эно (Henon map), предложен следующий метод распределения доступа пользователей к каналу связи. Вначале составляется каталог нестабильных периодических орбит различных периодов (иными словами, бифуркационная диаграмма). Часть этих орбит выбирается в качестве внутренних алфавитов пользователей каналом связи. Этот выбор осуществляется на основе того или иного выбранного критерия, такого, как минимизация общей корреляционной связи между выбираемыми орбитами. Управление процессом передачи информации по каналу связи осуществляется в соответствии со следующей схемой.
Этап 1. Осуществляется переход системы от хаотического движения по фазовому пространству к выбранной нестабильной периодической орбите.
Этап 2. Осуществляется поддержка движения системы в течение некоторого времени в окрестности этой орбиты.
Этап 3. Осуществляется обратный переход системы к хаотическому состоянию.
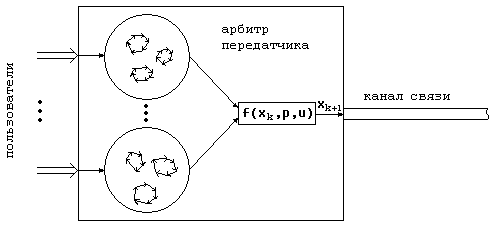
Рисунок 2 - Схема подключения арбитра передатчика
Существенной особенностью этого подхода является то, что арбитр приемника обеспечивает потенциальный доступ всей передаваемой информации каждому пользователю (рис. 2). Именно задача последних и состоит в том, чтобы распознать принадлежность передаваемого сигнала их внутреннему алфавиту. Отметим, что существование решения этой задачи состоит в выборе такой меры , и такого порога , чтобы для любой пары выделяемых пользователям алфавитов и было выполнено следующее условие
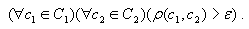 (1)
(1)
Ясно, что предложенный в [4] подход, в принципе, дает возможность построить некоторое распределение кодов между потенциально неограниченным числом пользователей. Однако вопрос о методах оценки качества такого распределения остается открытым. Более того, остается открытым сравнение уровня защиты
информации в предложенном в [4] подходе с уровнем, обеспечиваемым методами классической криптографии [8-11], что приобретает особую актуальность в связи с концепцией хаотического процессора, развитой в [12]. Эта задача и исследуется в настоящей работе. Ясно, что предложенный в [4] подход, в принципе, дает возможность построить некоторое распределение кодов между потенциально неограниченным числом пользователей. Однако вопрос о методах оценки качества такого распределения остается открытым. Более того, остается открытым сравнение уровня защиты информации в предложенном в [4] подходе с уровнем, обеспечиваемым методами классической криптографии [8-11], что приобретает особую актуальность в связи с концепцией хаотического процессора, развитой в [12]. Эта задача и исследуется в настоящей работе. Показано, что уже в классе кусочно-линейных отображений распределение кодов дает возможность обеспечить уровень защиты информации, сопоставимый с уровнем защиты информации, обеспечиваемым вычислительно стойкими нестационарными перестановочными шифрами.
Структура оставшейся части работы – следующая. П.1 содержит основные понятия и определения. В п.2 представлена схема организации многопользовательского доступа к каналу связи на основе распределения между пользователями циклических аттракторов одномерных кусочно-линейных отображений в качестве внутреннего алфавита канала. П.3 содержит анализ предложенной схемы. Заключение содержит ряд выводов.
1 Основные понятия
Для решения задачи записи информации в [6,7] предложено использовать кусочно-линейное одномерное отображение
Xn+1=f (xn )
, определяемое следующим образом. Пусть
bj=(j-0.5)•k -1 j=(1,...,K)
. Зафиксируем любую такую перестановку
(bi1 ,bi1 ,...,bik ) чисел
bi ,bi ,...,bk
, что
bi1 =b1
. На интервале
((j-1)•k -1; j•k -1) (j=1,..,k)
отображение
f
– это отрезок прямой, имеющий коэффициент наклона
s(0<s<1)
и проходящий через точку
bj =(bij , b(j+1)(mod n) ) .
Обозначим через
Sf динамическую систему, эволюция которой определяется рассмотренным выше кусочно-линейным отображением
f
, а через
Sk
– множество всех таких динамических систем при фиксированном значении k.
Рассмотрим динамическую систему
Sf ∈ Sk.
Выберем в качестве начального состояния системы
Sf
точку
x1 = b1 .
Тогда траектория системы
Sf
– это устойчивый цикл
Cf
, определяемый точками
b1 , b2 , ... , bk
(что проиллюстрировано на рис.3 для случая, когда
k =4 ).
Таким образом, динамическая система
Sf
однозначно восстанавливает перестановку
(bi1 ,bi1 ,...,bik ).
Отметим, что именно условие
s(0<s<1)
обеспечивает устойчивость цикла
Cf .
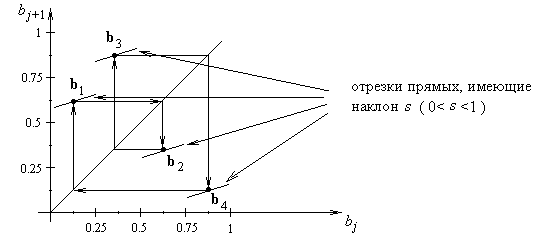
Рисунок 3 – Траектория динамической системы Sf ∈ S4 в случае, когда k =4 .
Выберем теперь в качестве начального состояния динамической системы
Sf
произвольную точку
x1∈ (0; k-1)
. Тогда траектория системы
Sf
– это цикл, получаемый сдвигом цикла
Cf
в горизонтальном направлении на величину
x1 - b1
. Итак, что при фиксированном значении
k
существует взаимно-однозначное соответствие между множеством
Sk
и множеством всех циклических перестановок элементов множества
(bi1 ,bi2 ,...,bik )
, откуда, в частности, вытекает, что
|Sk| =(k-1)!.
Покажем, что множество
Sk
легко преобразовать в метрическое пространство с легко вычислимой при параллельных вычислениях метрикой
ρ.
Определим на множестве {1,...,k}
семейство отображений
hr (r=1,0,...,k-1)
равенством
hr (i) = i+r(mod k).
Пусть динамической системе
Sfi ∈ Sk ( j=1,2)
соответствует циклическая перестановка
(bi1(j),bi2(j),...,bik(j))
. Положим
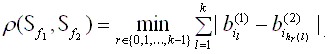 (2) (2)
Рассмотрим такую двухуровневую систему
C ( P0 , P1 ,..., Pk-1 , Pk )
из (k +1) -го процессора, что процессор
Pr (r=1,0,...,k-1)
, расположенный в 1-м уровне, вычисляет величину
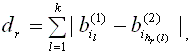 (3) (3)
а единственный процессор
Pk ,
, расположенный во 2-м уровне, вычисляет величину
min{d0 , d1 ,..., dk-1 , dk }
. Тогда при равномерном весе [13] система
C ( P0 , P1 ,..., Pk-1 , Pk )
осуществляет вычисление в соответствии с формулой (2) с временной сложностью
O(k) ( k → ∞ )
. Отметим, что при использовании этой меры достаточно легко обеспечит выполнение условия (1).
2 Схема доступа к каналу связи
Использование множества динамических систем
Sk , где параметр k определяется ожидаемым числом пользователей каналом связи, естественно приводит к схеме организации доступа к каналу связи, изображенной на рис. 4.
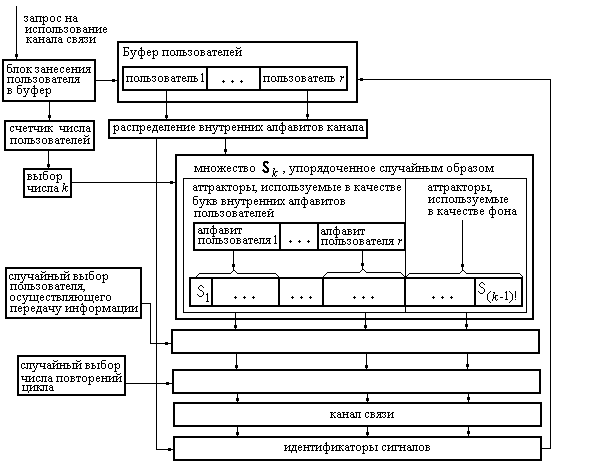
Рисунок 4 – Схема организации многопользовательского доступа к каналу связи.
Отметим, что именно под управлением блока занесения пользователей в буфер осуществляется связь между пользователями на уровне их внешних алфавитов. При этом вся та часть системы управления каналом связи, которая осуществляет управление передачей информации во внутренних алфавитах канала, является для пользователей «черным ящиком».
Рассмотрим, кратко, основные проблемы, связанные с предложенной схемой организации многопользовательского доступа к каналу связи.
Сложность, связанная с определением ожидаемого числа пользователей в «час пик», может быть преодолена следующим образом. Выбирается некоторое число
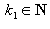 и осуществляется функционирование схемы обычным образом на множестве динамических систем
Sk1 Как только доля аттракторов, используемых в качестве «фона», становится меньше допустимого порога, выбирается некоторое такое число
и осуществляется функционирование схемы обычным образом на множестве динамических систем
Sk1 Как только доля аттракторов, используемых в качестве «фона», становится меньше допустимого порога, выбирается некоторое такое число
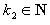 что
k2 ≠ k1
и вновь поступающие пользователи обслуживаются с помощью множества динамических систем
Sk2
и т.д. Так как
что
k2 ≠ k1
и вновь поступающие пользователи обслуживаются с помощью множества динамических систем
Sk2
и т.д. Так как
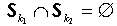 , если
k2 ≠ k1
, то конфликты между пользователями, связанные с распределением алфавитов, невозможны в принципе.
, если
k2 ≠ k1
, то конфликты между пользователями, связанные с распределением алфавитов, невозможны в принципе.
Прием информации, передаваемой по каналу связи, осуществляется всеми пользователями одновременно. Таким образом, величина задержки при приеме сигнала сводится к времени идентификации сигнала по принципу «свой/чужой». Ясно, что такая идентификация сигнала осуществима за линейное время при использовании одноуровневой схемы процессоров
C(P1 ,...,Pl )
где l – число символов алфавита, выделенных пользователю, а процессор
P1 (i=1,...,l)
предназначен для идентификации i-го символа, принадлежащего алфавиту, выделенному данному пользователю. Сложность возникает при выборе пользователя, осуществляющего в данный промежуток времени передачу информации. Эта сложность обусловлена следующими обстоятельствами.
Во-первых, необходимо одновременно контролировать все таймеры, фиксирующие время ожидания доступа пользователей к процессу передачи информации, не допуская превышения порога ни на одном из них.
Во-вторых, необходимо варьировать длину промежутка, выделяемого для передачи информации одним пользователем.
В третьих, необходимо контролировать объемы информации, подготовленной к передаче и помещенной в специальные буферы, чтобы не допустить их переполнения.
Таким образом, возникает необходимость многократного решения в реальном времени многопараметрической задачи теории расписаний. Следует, однако, отметить, что именно эта особенность присуща любому последовательно организованному доступу.
3 Анализ предложенной схемы
Предложенная схема организации многопользовательского доступа к каналу связи, с точки зрения классической криптографии, эквивалентна применению циклических перестановок, возможно, различной длины. Принципиально новые возможности, связанные с разрушением частот появления символов в сообщении, возникающие именно в процессе передачи циклических аттракторов, обеспечиваются следующими тремя типами действий:
1) вариация числа повторений цикла;
2) сопоставление различным пользователям попарно непересекающихся подмножеств множества Sk;
3) вариация параметра k.
А так как число пользователей r – случайная величина, то управление комбинацией этих действий дает возможность организовать функционирование канала связи, стойкое к любому частотному анализу.
Предложенная схема организации многопользовательского доступа к каналу связи предусматривает три уровня, связанные с переупорядочением элементов множеств.
Во-первых, это случайное упорядочение элементов множества
Sk
, где число возможных вариантов равно
((k-1)!)!
Во-вторых, это случайный выбор аттракторов, выделяемых конкретному пользователю, где число возможных вариантов равно
(k-1)!•(l!)-r
, в случае, когда число пользователей каналом связи равно
r
и каждому из них выделен
l
элементный алфавит (что, как правило имеет место при доступе к каналу связи).
В третьих, это случайное кодирование элементов внешнего алфавита выделенными пользователю аттракторами, где число возможных вариантов равно
(l!) r
, в случае, когда число пользователей каналом связи равно
r
и каждому из них выделен l -элементный алфавит.
Применение независимого переупорядочивания всех трех перечисленных выше типов приводит к числу вариантов, равному
((k-1)!)!(k-1)!
Ясно, что управление выбором этих вариантов с помощью поиска с линейной емкостной сложностью приводит к нестационарному шифрованию информации, передаваемой по каналу связи, практически эквивалентному применению одноразового блокнота [8].
ЗАКЛЮЧЕНИЕ
В работе решена задача организации многопользовательского доступа к каналу связи на основе циклических аттракторов динамических систем, эволюция которых определяется одномерными кусочно-линейными отображениями. Показано, что такая организация, по своей сути, эквивалентна применению нестационарных перестановочных шифров, определяемых циклическими перестановками. Секретным ключом предложенной системы управления доступом к каналу связи являются параметры, определяющие независимое упорядочение выбором на трех уровнях. Эффективное управление этим выбором дает возможность осуществить «экранирование» канала связи, вычислительно стойкое к любым пассивным внешним атакам.
Авторы выражают искреннюю благодарность чл.-корр. НАН Украины, профессору Ковалеву А.М. и с.н.с. ИПММ НАН Украины Щербаку В.Ф. за полезные обсуждения полученных результатов.
ЛИТЕРАТУРА
1. Schweizer J., Hasler M. Multiple access communications using chaotic signals // Proceedings of IEEE ISCAS’96, Atlanta, USA. – Vol. 3. – 1996.
2. Abel A., Bauer A., Kelber K., Schwarz W. Chaotic codes for CDMA application // Proceedings of ECCTD’97. – Vol. 1. – 1997.
3. Yang T., Chua L.O. Chaotic digital code-division multiple access (CDMA) // International Journal of Bifurcation & Chaos. – Vol. 7. – 1998.
4. Dmitriev A.S., Starkov S.O. Fine structure of chaotic attractor for multiple-access communications // Proceedings of the 7th International Workshop on Nonlinear Dynamics of Electronic Systems. – 1999.
5. Кузнецов С.П. Динамический хаос. – М.: Физматлит, 2001. – 296с.
6. Андреев Ю.В., Дмитриев А.С. Запись и восстановление изображений на одномерных динамических системах // Радиотехника и электроника. – Т. 39. – Вып. 1.–1994. – с.104-113.
7. Андреев Ю.В., Бельский Ю.Л., Дмитриев А.С. Запись и восстановление информации с использованием устойчивых циклов двумерных и многомерных отображений // Радиотехника и электроника. – Т. 39. – Вып. 1. – 1994. – с.104-113.
8. Shannon C.E. Communication Theory of Secrecy Systems // Bell System Technical Journal. – Vol. 28 – № 4. – 1949. – pp. 656-715.
9. Диффи У., Хеллмэн М.Э. Защищенность и имитостойкость: Введение в криптографию // ТИИЭР. – Т.67. – № 3. – 1979. – с. 71-109.
10. Шнайер Б. Прикладная криптография. Протоколы, алгоритмы, исходные тексты на языке СИ. – М.: ТРИУМФ, 2003. – 816с.
11. Молдовян А.А., Молдовян Н.А., Гуц Н.Д., Изотов Б.В. Криптография. Скоростные шифры. – СПб.: БХВ-Петербург, 2002. – 496с.
12. Андреев Ю.В., Дмитриев А.С., Куминов Д.А. Хаотические процессоры // Зарубежная радиоэлектроника. – Т. 42. – Вып. 10. – 1994. – с.50-79.
13. Ахо А., Хопкрофт Дж., Ульман Дж. Построение и анализ вычислительных алгоритмов. – М.: Мир, 1979. – 536с.
14. Скобелев В.Г. Анализ дискретных систем. – Донецк: ИПММ НАНУ, 2003. – 172с.
15. Рейнгольд Э., Нивергельт Ю., Део Н. Комбинаторные алгоритмы. Теория и практика. – М.: Мир, 1980. – 476с.
Скобелев В.Г., Ткаченко А. В. Многопользовательский доступ к каналу связи на основе циклических аттракторов.
// Искусственный интеллект 3`2004 – Донецьк: ІПШІ "Наука і освіта". – 2004. – с.836-843.
|

 /
/

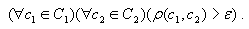 (1)
(1)

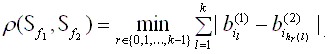 (2)
(2)
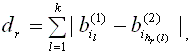 (3)
(3)

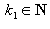 и осуществляется функционирование схемы обычным образом на множестве динамических систем
Sk1 Как только доля аттракторов, используемых в качестве «фона», становится меньше допустимого порога, выбирается некоторое такое число
и осуществляется функционирование схемы обычным образом на множестве динамических систем
Sk1 Как только доля аттракторов, используемых в качестве «фона», становится меньше допустимого порога, выбирается некоторое такое число
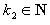 что
k2 ≠ k1
и вновь поступающие пользователи обслуживаются с помощью множества динамических систем
Sk2
и т.д. Так как
что
k2 ≠ k1
и вновь поступающие пользователи обслуживаются с помощью множества динамических систем
Sk2
и т.д. Так как
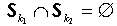 , если
k2 ≠ k1
, то конфликты между пользователями, связанные с распределением алфавитов, невозможны в принципе.
, если
k2 ≠ k1
, то конфликты между пользователями, связанные с распределением алфавитов, невозможны в принципе.