| Автобиография | Магистерская работа | Библиотека |
| Ссылки | Индивидуальное задание | Отчет о поиске |

|
Ткаченко Александр Валерьевич
Разработка нейросетевой системы управления котлом энергоблока |
|
Ткаченко В.Н., Ткаченко А. В. Abstract. Tkachenko V.N., Tkachenko A.V. Parametric identification of nonlinear systems under conditions of bifurcation. Problem of parametric identification of nonlinear systems under conditions of bifurcation is considered. Process of autocatalytic reaction is given as example. Qualitative analysis of the system behavior is done. Points of bifurcations of equilibrium states are found and bifurcation diagrams are built. Analysis results make possible to isolate districts of the parameters where they can be searched by a gradient procedures.
Анализ исследований по рассматриваемой проблеме.
Совершенствование систем управления технологическими процессами, улучшение их качества в настоящее время идет по пути повышения точности используемых математических моделей и методов их идентификации [1]. При этом для создания более совершенных систем управления необходимо использовать более полные и точные модели, учитывающие нелинейные эффекты. Для параметрической идентификации линейных систем различной сложности предложены достаточно простые и эффективные методы, основанные на идее метода наименьших квадратов [2], а также алгоритмов реального масштаба времени таких как рекуррентный метод наименьших квадратов и его модификации, методы стохастической аппроксимации [3] и др. Существует ряд приближенных инженерных методов, среди которых наиболее эффективными являются метод площадей (метод Симою) и графо-аналитический метод [3]. Эти методы широко используются для идентификации моделей объектов автоматики по кривым разгона, полученным в виде реакции на единичный входной сигнал.
Постановка задачи и цели исследований.
Целью данной работы является исследование свойств системы при изменении ее параметров на примере простейшей нелинейности в виде квадратичного полинома в правой части обыкновенного дифференциального уравнения и особенностей применения градиентных методов параметрической идентификации в условиях бифуркации положений равновесия и возможных скачков на качественно другие траектории при движении в пространстве параметров системы.
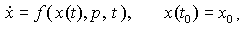 (1)
(1)
Постановка задачи и цели исследований.
Целью данной работы является исследование свойств системы при изменении ее параметров на примере простейшей нелинейности в виде квадратичного полинома в правой части обыкновенного дифференциального уравнения и особенностей применения градиентных методов параметрической идентификации в условиях бифуркации положений равновесия и возможных скачков на качественно другие траектории при движении в пространстве параметров системы.
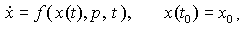 (1)
(1)
где f – нелинейная функция, зависящая от вектора параметров p и времени t .
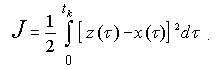 (2)
(2)
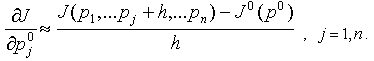 (3)
(3)
Новое приближение для вектора параметров определим как
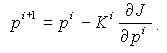 (4)
(4)
Соотношение (4) дает итеративный процесс улучшения оценок параметров до тех пор, пока будет уменьшаться функционал невязки. В зависимости от способа выбора
K i получаем различные модификации градиентных процедур. В частности, по методу наискорейшего спуска
K i выбирается из условия
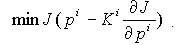 (5)
(5)
Таким образом, любой градиентный метод идентификации сводится к движению в пространстве параметров системы с целью поиска наилучших в смысле (2) параметров системы и, в общем случае, не предполагает контроля возможных скачков на качественно другие типы решений нелинейной системы. В этих условиях сходимость градиентной процедуры гарантировать невозможно. В связи с этим необходимо исследовать все возможные качественно различные решения нелинейной системы и установить область параметров P x , траектории которой будут соответствовать на качественном уровне характеру результатам измерений z(t) и априорным представлениям о поведении моделируемой системы.
Качественный анализ поведения нелинейной системы.
В качестве простейшего примера нелинейной системы рассмотрим реактор, в котором происходит автокаталитическая реакция. Вещество подается в реактор с постоянной скоростью и удаляется через мембрану со скоростью пропорциональной концентрации. В автокаталитической реакции скорость возникновения вещества пропорциональна квадрату
его концентрации. Таким образом, на основе материального баланса скорость изменения концентрации вещества описывается следующим нелинейным дифференциальным уравнением
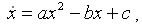 (6)
(6)
где x - концентрация вещества;
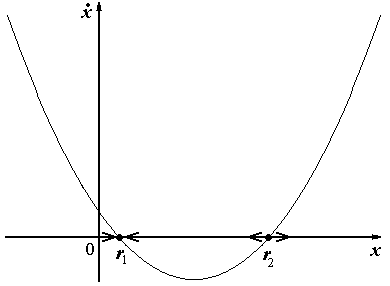
Рисунок 1 – фазовый портрет правой части уравнения (6).
Проведем качественный анализ динамики концентрации вещества в реакторе. С этой целью построим фазовый портрет правой части уравнения (6) (рис. 1). Получим точки равновесия уравнения (6), приравняв правую часть уравнения нулю. В зависимости от значений коэффициентов уравнения имеется три случая:
1. Предположим что коэффициенты таковы, что дискриминант квадратного уравнения больше нуля и имеются два различных действительных корня
r1 , r2 (r1 , r2 ) .
В точках равновесия рис.1 расставим стрелочки, указывающие на возрастание траектории
x(t), если правая часть положительна, и убывание траектории, если правая часть отрицательна. Получим, что состояние равновесия в точке
r1 является аттрактором [4] , а состояние равновесия в точке
r2 является репеллером.
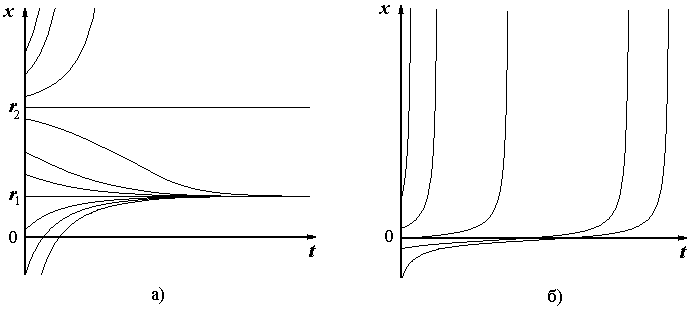
Рисунок 2 – Качественный вид решений уравнения (6): а) правая часть уравнения (6) имеет два различных действительных корня; б) правая часть уравнения (6) имеет комплексно-сопряженные корни.
При этом неявное аналитическое решение в общем виде имеет вид
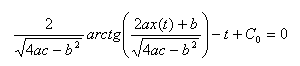 (7)
(7)
2. В случае существования одного действительного корня
r0 состояние равновесия в этой точке становится неустойчивым, а поведение траекторий решения будет определяться начальным значением
x0 : если x0 ≤ r0 : , то траектории будут асимптотически стремится к состоянию равновесия, в противном случае – буду неограниченно возрастать.
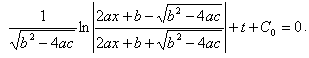 (8)
(8)
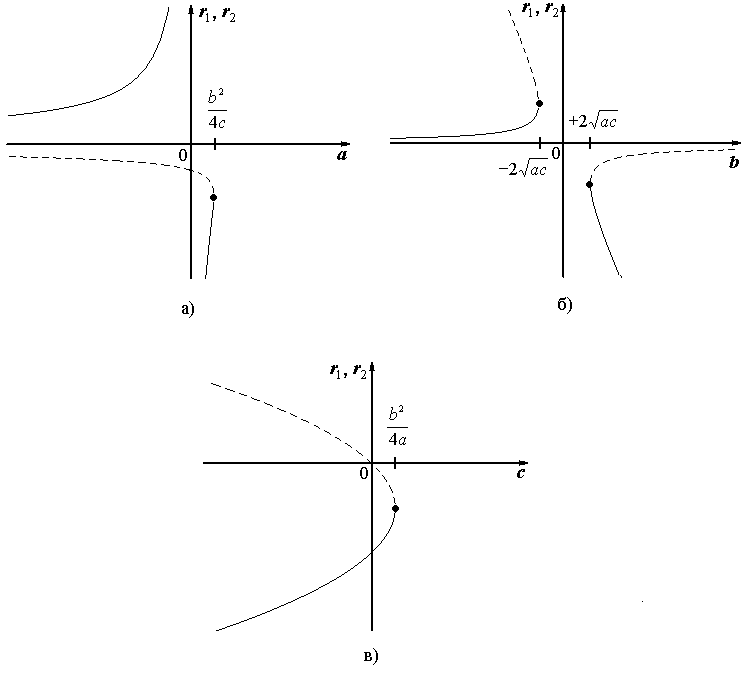
Рисунок 3 – диаграммы бифуркаций точек равновесия уравнения (6) в зависимости от: а) параметра a; б) параметра b; в) параметра c; (сплошная линия соответствует устойчивым точкам равновесия, а пунктирная - не устойчивым).
Анализ диаграмм бифуркации при изменении параметров системы.
Рассмотрим поведение изучаемой системы при изменении параметров a, b ,c в достаточно широком диапазоне. Приравняем правую часть уравнения (6) к нулю и выполним анализ изменения числа точек равновесия при изменении параметров. Точки бифуркации числа состояний равновесия могут быть найдены из условия равенства нулю дискриминанта квадратного уравнения
При
D > 0
имеется два состояния равновесия, при
D < 0
состояния равновесия отсутствуют. Разрешая соотношение (9) относительно варьируемого параметра, легко определить точки бифуркаций по каждому параметру:
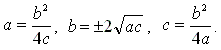 (10) (10)
Кроме того, при a=0 появляется новое состояние равновесия r=c/b и система (6) становится линейной. На рис. 3 представлены диаграммы бифуркаций по параметрам a, b, c, позволяющие установить диапазоны изменения параметров, которым соответствуют качественно различные траектории. На основе качественного анализа решений нелинейной системы, а также результатов анализа диаграмм бифуркации можно определить область Px , траектории которой будут соответствовать на качественном уровне характеру результатам измерений z(t). После чего можно реализовать устойчивую процедур градиентной минимизации функционала (2) и получить ожидаемый результат. Выводы. В работе рассмотрена проблема параметрической идентификации систем, описываемых нелинейными обыкновенными дифференциальными уравнениями. На примере простейшей нелинейности выполнен качественный анализ, в результате которого показано возможное разнообразие поведение модели при изменении начальных условий, а также изменение числа точек равновесия и их свойств устойчивости в условиях варьирования параметров системы. Найденные точки бифуркации состояний равновесия и построенные диаграммы бифуркации позволяют установить область параметров Px , в которой целесообразно искать параметры системы на основе градиентных методов. Литература
1. Идентификация объектов систем управления технологическими процессами/ Киричков В.Н. – К.: Вища школа, 1990, - с.187.
Ткаченко В.Н., Ткаченко А. В. Параметрическая идентификация нелинейных систем в условиях бифуркации. // Наукові праці Донецького державного технічного університету. Сер. обчислювальна техніка та автоматизація, випуск 65. – Донецьк: ДонНТУ. – 2004. – с.57-62. |
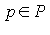 где P - область допустимых значений параметров. На практике, однако, не всегда можно задать область на основе априорной информации о рассматриваемой предметной области.
где P - область допустимых значений параметров. На практике, однако, не всегда можно задать область на основе априорной информации о рассматриваемой предметной области.