Введение.

      Изучение структуры головного мозга и механизмов его работы привило к развитию новых вычислительных методов, основанных на биохимических понятиях и пригодных для решения таких сложных задач, как распознавание образов, моделирование, быстрое преобразование информации (параллельные вычислительные процессы), идентификация и управление. Этими новыми вычислительными моделями стали искусственные нейронные сети (ИНС).
      Еще в начале XX века И.П. Павлов открыл элементарный блок мозга — условный рефлекс. Он считал условный рефлекс одним из основных атомов" интеллектуальных процессов, происходящих в коре головного мозга. Им и другими учеными были выдвинуты в свое время различные гипотезы механизмов адаптивности центральной нервной системы.
      Впервые формализованную модель искусственной нейронной сети предложили У.С. Мак-Каллоком и У. Питтсом (1943) в фундаментальной работе о логическом анализе нервной деятельности. Ими была разработана теория идеализированных нейронных сетей как конечных автоматов, где нейроны служат "универсальными элементами", удовлетворяющими принципу "все или ничего". Дж. фон Нейман оценил результат исследования того, как можно с помощью "формальных нервных сетей", состоящих из "формализованных нейронов и связей", реализовать психологические функции. У.С. Мак-Каллок и У. Питтс показали и строго обосновали возможность реализации такой сетью ".. .любого функционирования ... при условии, что оно поддается сколь нибудь логически точному и однозначному описанию конечным числом слов". Впоследствии в ряде других работ и прежде всего в работе С.К. Клини «Представление событий в нервных сетях и конечных автоматах» (1956) было показано, что "единственным существенным ограничением, делающим невозможным представление их в виде конечных сетей, являются события, определение которых зависит от временных координат". В то же время "... любое событие, которое можно описать как одно из определенного множества возможных последовательностей на входе, может быть представлено в виде такой сети".
      Исследователи, высказывавшие другие точки зрения на организацию "моделей мозга", относящихся к генотипным моделям, исходили из того, что свойства нейронов как и в "идеализированных сетях" Мак-Каллока и Питтса, полностью определены, но топология сетей, в противоположность аксиоматике Мак-Каллока и Питтса, выявления лишь частично в результате наложения ограничений. При "генотипном" подходе функциональные характеристики модели выступают в качестве конечной цели анализа, а исходной является сама физическая система. В другом, монотипном подходе, функциональные свойства модели обычно постулируются в качестве исходных.
      В последующем развитии теории искусственных нейросетей "генотипный" подход получил преимущественное развитие. Здесь наиболее известным результатом стала модель Хебба (1949). Д. Хебб предположил существование процесса, благодаря которому нейроны, достаточно часто возбуждаемые одновременно, связываются в "ассоциации клеток" и "фазовые последовательности", образующие функциональные структуры. Этим структурам под воздействием определенного "стимула" соответствует некоторый образ или ощущение. Д. Хеббом и другими исследователями была предложена модель, впоследствии названная синапсом Хебба. В ее механизме учитывается корреляция активности афферентного (входного) синапса (соединения) и эфферентного (выходного) нейрона, так что если корреляция положительна, то контакт между передающим и принимающим нейронами улучшается; т.е. происходит нарастание синапса; если же корреляция отрицательна, то чувствительность синаптической мембраны уменьшается.
      Теории Хебба, Мак-Каллока-Питтса и накопленные со временем экспериментальные данные в психологии и физиологии привели в 1957 г. американского ученого Ф. Розенблатта к модели "мозгоподобного" устройства, названного им персептроном (от лат. perceptio — восприятие). Ф. Розенблатт определяет персептрон как "некоторое множество элементов ("нейронов"), генерирующих сигналы, связанных в единую сеть". Логические свойства персептрона определяются:
    - его топологической структурой, т.е. связями между "нейронами";
    - набором алгоритмов, управляющих генерацией и передачей сигналов;
    - набором функций памяти или алгоритмов преобразования свойств
    - сети в результате активности.
      В отличие от других моделей нейронных сетей, персептрон Розенблатта допускал большую свободу установления связей по сравнению с сетями с заранее заданными логическими алгоритмами. Основная Каллока-Питса в задачах нейрофизиологии системами, действующими на основе статистического описания слоев элементов пресептрона. Впоследствии именно модель персептрона привлекла наибольшее внимание специалистов.
      В 1960 г. Б Уидроу и М Хофф разработали модель нейрона, которая обучалась быстрее и более точно, чем персептрон Она получила название адалины (сокр. от adaptive linear neuron). Алгоритм настройки основывался на методе наименьших квадратов и получил название " - правило". Этим алгоритмом впервые была введена концепция обучения "с учителем".
      Простая линейная сеть madaline (many adaline) была рассмотрена М. Минским и С. Пейпертом в опубликованной ими в 1969 г книге. В ней было положено начало строгому анализу персептронных схем. Но пессиместические выводы, последовавшие в результате этих исследований, остановили процесс изучения проблемы почти на 20 лет. Утверждалось, что однослойные линейные сети имеют ограниченные возможности (что в принципе верно), а обучение многослойных сетей непродуктивно. Авторитет М. Минского и С Пейперта был настолько велик, что их вывод стал своеобразным приговором, и интерес к проблеме искусственных нейронных сетей был утрачен на многие годы И только в 1982 г. появилась работа Дж. Хопфилда, где он описал специальную динамическую структуру, разработанную им для решения оптимизационных задач, получившую название сети Хопфилда. Для ее обучения были разработаны различные методы и алгоритмы. В 1986 г. исследовательская группа по параллельным вычислениям (группа PDP: Д. Румельхарт, Дж. Хинтон, Р Вильяме, США) разработала вычслительную процедуру обучения многослойных нейронных сетей (МНС), получившую название "error back propagation method" — метод обратного распространения ошибки. После этого интерес к искусственным нейронным сетям и их практическому применению приобрел характер настоящего бума.
      В развитие теории нейронных сетей значительный вклад внесли советские и российские ученые Еще в 1966 году советскими учеными А.Я. Червоненкисом и В.Н. Вапником были разработаны основы т.н. "теории размерности", позволившей дать оценку возможностей обучающихся систем вообще и нейронных сетей, в частности. Фундаментальные исследования в 60-е годы в области персептронных систем были выполнены акад. АН СССР В.М. Глушковым и чл.-корр. АН УССР А.Г. Ивахненко. Раз в два—четыре года в г. Ростове-на-Дону проводились Всесоюзные с международным участием конференции по нейрокибернетике, организатором которых был проф. А.Б. Коган, возглавлявший в 60—80-е годы нейрофизиологические исследования в организованном им НИИ нейрокибернетики при Ростовском государственном университете и скоординировавший исследования в этой области во всесоюзном масштабе. Проф. А.В. Каляев еще в 1975 г организовал лабораторию нейроноподобных структур в НИИ многопроцессорных вычислительных систем при Таганрогском радиотехническом институте, основной задачей которой стала разработка, создание и исследование адаптивных самоорганизующихся нейроподобных систем искусственного интеллекта. Отметим, в частности, ряд выполненных в ней пионерских работ проф. Ю.В. Чернухина и его сотрудников по нейропроцессорным сетям, ориентированным на использование в системах искусственного интеллекта адаптивных автономных роботов.
      В развитие современных методов обучения многослойных нейронных сетей наряду с французским ученым ле Куном большой вклад внес проф. А.Н. Горбань (г Красноярск), сформулировавший и обосновавший "принцип двойственности", позволяющий организовать экономные вычисления векторов градиента сложных функций. Ряд работ по многослойным системам распознавания образов был опубликован еще в начале 70-х годов проф. А.И Галушкиным (Москва). Перечень достижений в области нейрокибернетики, полученных советскими и российскими учеными, может быть продолжен.
      Важный класс искусственных нейронных сетей был введен финским ученым Т. Кохоненом в 1987 г. под названием "самоорганизующиеся отображения состояний с сохранением топологии сенсорного пространства" или "карта самоорганизации". В теории сетей Кохонена используется алгоритмическая теория адаптивных систем, в основном развитая в трудах акад Я.З. Цыпкина.
      Нервная система животных и человека стала прототипом искусственных нейронных сетей. Ее элементами служат базовые процессорные элементы – аналоги биологических нейронов в смысле имитации их наиболее важных элементарных функций. ИНС представляют собой устройство, в которое входит большое число связанных между собой базовых элементов. Искусственная нейронная сеть, как и ее прототип – биологическая нервная сеть, может менять свое поведение в зависимости от внутренних и внешних воздействий, и это вызывает к ним повышенный интерес. После предъявления входных сигналов вместе с требуемыми выходными сеть настраивается (обучается) так, чтобы обеспечить требуемую реакцию. При этом отклик сети после обучения может быть либо нечувствителен к небольшим изменениям входных сигналов, либо проявлять обобщающие свойства. Важно отметить, что ИНС делает верный отклик автоматически благодаря своей структуре, а не с помощью специально составленных компьютерных программ.
      Потенциальные приложения искусственных нейронных сетей просматриваются в тех задачах, когда в силу неопределенности, например из-за недостатка информации или «шума», традиционные решения не эффективны, а обычные вычисления непомерно трудоемки или же не адекватны решаемой задаче. Трудности использования таких состоят в отсутствии наглядной возможности объяснить как сеть решает поставленную задачу. Ф Уссермен пишет: “… внутренние представления получающиеся в процессе обучения, … настолько сложны, что их невозможно проанализировать за исключением самых простых случаев. Это напоминает нашу неспособность объяснить, как мы узнаем человека, несмотря на различия в расстоянии, угле зрения, освещения и на прошедшие годы” [2].
      В настоящее время разработано и исследовано несколько десятков искусственных нейронных сетей. Но базовыми, принципиально различными типами являются три типа сетей, соответствующим, в основном, трем методам обучения: самоорганизующиеся сети Кохонена с обучением без «учителя»; динамические сети Хопфилда с обучением по методу последовательного подкрепления знаний; сети прямого распространения (персептронные) с обучением с «учителем».

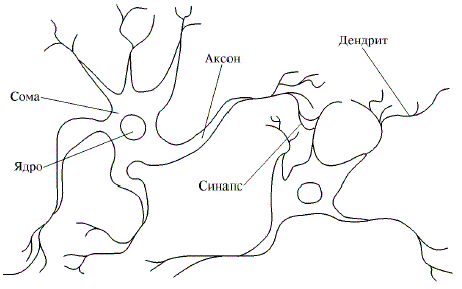
Рис 1.1. Взаимосвязь биологических нейронов.

      Синапсы являются элементарной структурой и функциональным узлом между двумя нейронами (волокна одного нейрона и дендрит другого). Когда импульс достигает синаптического окончания, высвобождаются определенные химические вещества, называемы нейротрансмиттерами. Нейротрансмиттерами диффундируют через синаптическую щель, возбуждая или затормаживая, в зависимости от типа синапса, спосбность нейрона приемника генерировать электрические импульсы. Результативность синапса может настраиваться проходящими через него сигналами, так что синапсы могут обучаться в зависимости от активности процессов, в которых они участвуют.
      Нервная система человека имеет ошеломляющую сложность. Около 10¹¹ нейронов участвуют в примерно 10¹⁵ передающих связях, имеющих длину метр и более. Каждый нейрон обладает многими качествами, общими с другими элементами тела, но его уникальной способностью является прием, обработка и передача электрохимических сигналов по нервным путям, которые образуют коммуникационную систему мозга.

1.2 Искусственный нейрон.

      Соответственно с биологической моделью каждый нейрон можно считать своеобразным процессором: он суммирует с соответствующими весами сигналы, приходящие от других нейронов, выполняет над суммой нелинейную решающую функцию. Таким образом, структурная схема модели нейрона представлена на рис. 1.2.

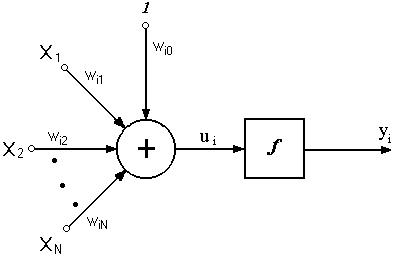
Рис 1.2. Структура искусственного нейрона.

i - индекс нейрона. Входные сигналы x_j (j=1,2,..N) суммируются с учетом соответствующих весов w_ij (сигнал поступает от узла i к узлу j) в сумматоре, после чего результат складывается с пороговым значением w_i0 и делается нелинейное преобразование. Выходной сигнал y_i определяется при этом зависимостью:

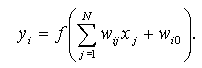(1.1)

      Аргументом функции выступает суммарный сигнал 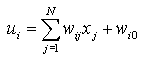. Функция f(u_i ) называется функцией активации.
      Коэффициенты w_ij представляют собой веса синаптических связей. Положительное значение соответствуют возбуждающим синапсам, отрицательное значение – тормозящим синапсам, тогда как w_ij=0 свидетельствует о отсутствии связи.
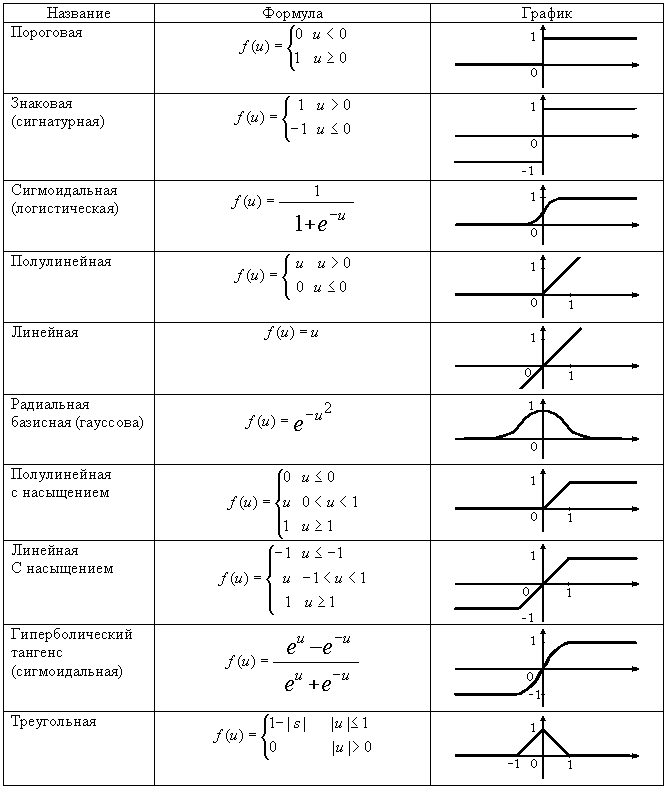
Примеры функций активации представлены в таблице 1.1.

      Таблица 1.1Функции активации нейронов

2. Однонаправленные многослойные сети сигмоидального типа.

      Объединенные между собой нейроны образуют систему, которая в дальнейшем будет называться искусственной нейронной сетью. В зависимости от способа объединения нейронов они могут быть сетями однонаправленными либо рекуррентными (с обратной связью). В ИНС нейроны объединяются в слои, в которых происходит параллельная обработка сигнала.

2.1 Однослойная сеть.      

Однослойную сеть образуют нейроны расположенные в одной плоскости (рис. 2.1). Слой имеет N входов и состоит из M нейронов. Каждый нейрон имеет поляризацию (связь w_i0 , по которой поступает единичный сигнал), а также множество связей w_ij , по которым поступают входные сигналы x_j и выход y_i .

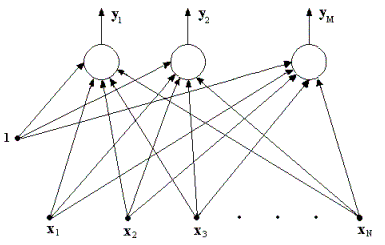
Рис 2.1. Структура однослойной сети прямого распространения.

      Работа слоя описывается формулой (1.1).
      Значения весов подбираюсь в процессе обучения сети. При обучении с учителем выходные сигналы y_i приближаются к ожидаемым значениям d_i . Мерой близости считается значение целевой функции

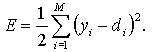(2.1)

      При использовании p обучающих векторов < x, d > для обучения сети включающей M нейронов, целевую функцию можно определить эвклидовой метрикой вида

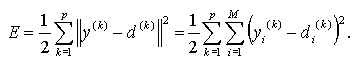(2.2)

      Выходные сигналы нейрона y_i являються функциями весов w_ij , значения которых уточняются в процессе обучения по критерию минимизации целевой функции.
      Расположенные на одном уровне нейроны функционируют независимо друг от друга, поэтому возможности такой сети ограничиваются свойствами отдельных нейронов. Выходной y_i сигнал зависит от расположения вектора x , в гиперпространстве, разделяемой гиперплоскостью определяемой весовыми коэффициентами.

2.2 Многослойный персептрон.      

Многослойная сеть состоит из нейронов, расположенных на разных уровнях, причем, помимо входного и выходного слоев, имеется еще, как минимум, один внутренний, т.е. скрытый слой (рис. 2.2).

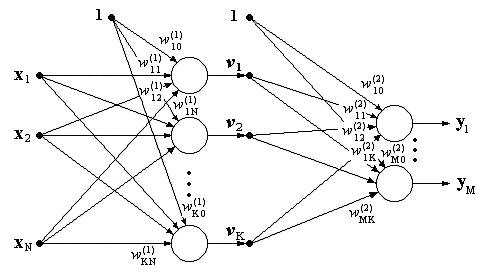
Рис 2.2. Обобщенная структура двухслойной нейронной сети (с одним скрытым слоем).

      Выходные сигналы скрытого слоя обозначим v_j (j=1, 2, …, K) , a выходного слоя yj (j=1, 2, …, M). Выходной сигнал скрытого слоя описывается функцией

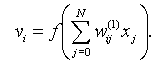(2.3)

      В выходном слое k-й нейрон вырабатывает выходной сигнал, определяемый как

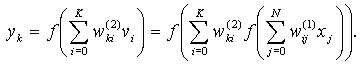(2.4)

      Цель обучения состоит в подборе таких весовых коэффициентов для всех слоев, чтобы при заданном входе x_i получить на выходе значения y_i , которые с требуемой точность будут совпадать с ожидаемыми d_i для i=1, 2, …, М.

2.3 Алгоритм обратного распространения ошибки.

      Алгоритм обратного распространения ошибки определяет стратегию подбора весов многослойной сети с применением градиентных методов оптимизации. В качестве целевой функции можно использовать формулы (2.1) и (2.2). Уточнение весов может производится после предъявления каждой обучающей выборки (так называемый режим «онлайн») либо однократно после предъявления всех выборок составляющих цикл обучения (режим «оффлайн»). В дальнейшем будем использовать целевую функцию вида (2.1), которая соответствует актуализации весов после предъявления каждой выборки.
      Если принять, что целевая функция непрерывна и унимодальна, то наиболее эффективными оказываются градиентные методы оптимизации, согласно которым уточнение вектора весов (обучение) производиться по формуле

w (t + 1) = w (t) + Δ w (2.5)

где

Δ w = ηρ(w)   (2.6)

      ηρ - коэффициент обучения, а ρ(w) - направление минимизации в многомерном пространстве . Начальные значения весов вначале берутся случайными.
      Обучение многослойной сети с применением градиентных методов требует определения вектора градиента относительно весов всех слоев сети, для определения направления ρ(w).
      В качестве направления ρ(w) в простейшем случае будем использовать градиент ошибки

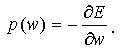(2.7)

      Для упрощения будем рассматривать функцию вида (2.1) и нейронную сеть с одним скрытым слоем

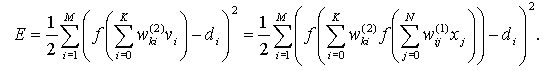(2.8)

      Далее компоненты градиента рассчитываются дифференцированием формулы (2.8).В первую очередь определяются производные весов нейронов выходного слоя

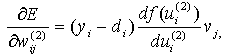(2.9)

      где 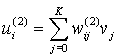. Если внести обозначение 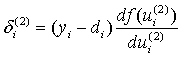, то

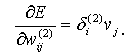(2.10)

      Компоненты градиента относительно нейронов скрытого слоя определяются по тому же принципу

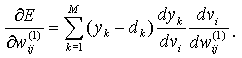(2.11)

      При конкретизации составляющих этого выражения получаем

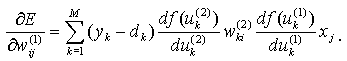(2.12)

      Если ввести обозначение

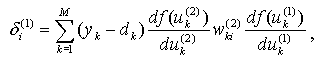(2.13)

то получим выражение определяющее компоненты градиента относительно скрытого слоя

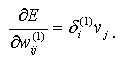(2.14)

Литература

1. Осовский С. Нейронные сети для обработки информации: Пер. с польского. М: Финансы и статистика, 2002. 344 с.
2. Уоссермен Ф. Нейрокомпьютерная техника: Теория и практика: Пер. с англ.- M.: Мир, 1992.
3. Сигеру Омату, Марзуки Халид, Рубия Юсоф Нейроуправление и его приложения. М: Радиотехника, 2000. 272 с.
4. Терехов В.А. Ефимов Д.В. Тюкин И.Ю. Нейросетевые системы управления. -М: Радиотехника, 2002. 480 с.
5. Нейроматематематика: под ред. А.И. Галушкин. М.: Радиотехника, 2002. 448 с.