ЦИФРОВАЯ ОБРАБОТКА ИЗОБРАЖЕНИЙ
1. ТЕОРЕТИЧЕСКИЙ РАЗДЕЛ
1. Ввод и представление изображений
Принципиальными вопросами в теории обработки изображений являются вопросы: формирования, ввода, представления в компьютере и визуализации. Получение изображений в виде электронно-микроскопических снимков с помощью электронного микроскопа описаны в работе. Область ввода видеоинформации представляет собой прямоугольное поле, задаваемое верхней, нижней, левой и правой границами. Форму поверхности можно описать в виде функции расстояния F(x,y) от поверхности до точки изображения с координатами x и y. Учитывая, что яркость точки на изображении зависит исключительно от яркости соответствующего участка поверхности, то можно считать, что визуальная информация с определенной степенью точности отражает состояние яркости или прозрачности каждой точки. Тогда под изображением понимается ограниченная функция двух пространственных переменных f(x,y), заданная на ограниченной прямоугольной плоскости Оху и имеющая определенное множество своих значений. Например, черно-белая фотография может быть представлена как f (x,y) ³ 0 , где 0£ x £ a, 0£ y £ b , где f (x,y) – яркость (иногда называемая оптической плотностью или степенью белизны) изображения в точке (x,y); a – ширина кадра, b – высота кадра.
В связи с тем, что цифровая память компьютера способна хранить только массивы данных, сначала изображение преобразуется в некоторую числовую форму (матрицу). Ввод изображений в память компьютера осуществляется с помощью видео датчиков. Видео датчик переводит оптическое распределение яркости изображения в электрические сигналы и далее в цифровые коды. Поскольку изображение является функцией двух пространственных переменных x и y, а электрический сигнал – функцией одной переменной t (времени), то для преобразования используется развертка. Например, при использовании телевизионной камеры изображение считывается по строкам, при этом в пределах каждой строки зависимость яркости от пространственной координаты x преобразуется в пропорциональную зависимость амплитуды электрического сигнала от времени t. Переход от конца предыдущей строки к началу следующей происходит практически мгновенно.
Ввод изображений в компьютер неизбежно связан с дискретизацией изображений по пространственным координатам x и y и квантованием значения яркости в каждой дискретной точке. Дискретизация достигается с помощью координатной сетки, образованной линиями, параллельными осям x и y декартовой системы координат. В каждом узле такой решетки делается отсчет яркости или прозрачности носителя зрительно воспринимаемой информации, которая затем квантуется и представляется в памяти компьютера. Элемент изображения, полученной в процессе дискретизации изображения, называется пиксел. Для качественного представления полутонового изображения достаточно 28 = 256 уровней квантования, т.е. 1 пиксел изображения кодируется 1 байтом информации.
В цифровом комплексе IBAS-2000 информация, содержащаяся в изображении, представляется в виде различных уровней серой шкалы для отдельных точек изображения. Максимальный объем видеоинформации ограничивается количеством пикселов (512х512 или 768х512), а также количеством уровней серой шкалы – 256: 0 – черный, 255 – белый. Одновременно в видеопамяти может быть сформировано от 8 до 56 различных ячеек в зависимости от размера изображения. Видеопроцессор имеет матричную структуру, обеспечивает 10 млн. умножений в сек., изображение в нем представляется в векторной форме. Полутоновое или цветное изображение может быть выведено на монитор или распечатано.
2. Улучшение контраста
Слабый контраст – наиболее распространенный дефект фотографических, сканерных и телевизионных изображений, обусловленный ограниченностью диапазона воспроизводимых яркостей. Под контрастом обычно понимают разность максимального и минимального значений яркости. Путем цифровой обработки контраст можно повысить, изменяя яркость каждого элемента изображения и увеличивая диапазон яркостей. Для этого разработано несколько методов.
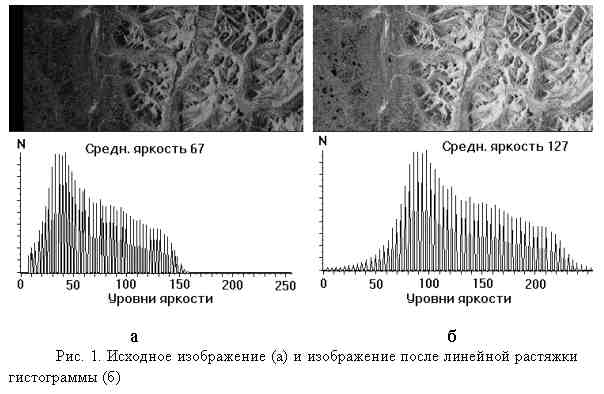
Пусть, например, уровни некоторого черно-белого изображения занимают интервал от 6 до 158 со средним значением яркости 67 при возможном наибольшем интервале значений от 0 до 255. На рисунке 1а приведена гистограмма яркостей исходного изображения, показывающая, сколько пикселов N с близким значением яркости f попадает в интервал от fi до f +∆fi. Это изображение является малоконтрастным, превалирует темный оттенок. Возможным методом улучшения контраста может стать так называемая линейная растяжка гистограммы (stretch), когда уровням исходного изображения, лежащим в интервале [fмин, fмакс], присваиваются новые значения с тем, чтобы охватить весь возможный интервал изменения яркости, в данном случае [0, 255]. При этом контраст существенно увеличивается (рис. 1б). Преобразование уровней яркости осуществляется по формуле:
![]() (1)
(1)
где fi - старое значение яркости i-го пиксела, gi - новое значение, a, b - коэффициенты. Для рис. 1а fмин = 6, fмакс = 158. Выберем a и b таким образом, чтобы gмин = 0, gмакс = 255. Из (1) получаем: a = - 10,01; b = 1,67.
 |
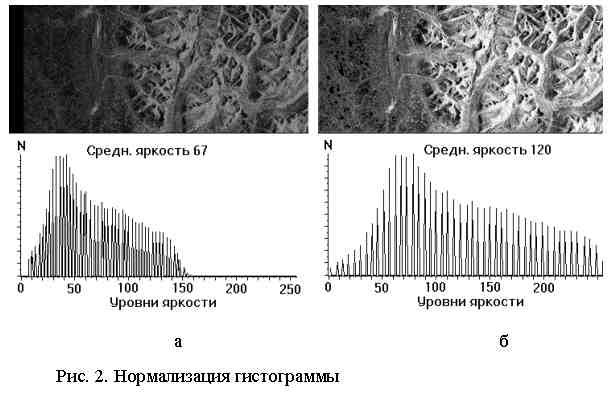
Еще более можно улучшить контраст, используя нормализацию гистограммы. При этом на весь максимальный интервал уровней яркости [0, 255] растягивается не вся гистограмма, лежащая в пределах от fмин до fмакс, а её наиболее интенсивный участок (fмин', fмакс'), из рассмотрения исключаются малоинформативные "хвосты". На рис. 2б исключено 5% пикселов.
 |
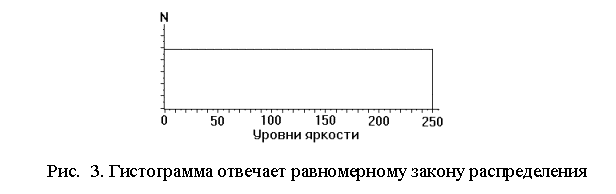
Целью выравнивания гистограммы (эту процедуру называют также линеаризацией и эквализацией - equalization) является такое преобразование, чтобы, в идеале, все уровни яркости приобрели бы одинаковую частоту, а гистограмма яркостей отвечала бы равномерному закону распределения (рис. 3).
 |
Пусть изображение имеет формат: N пикселов по горизонтали и M по вертикали, число уровней квантования яркости равно J. Общее число пикселов равно N ·M, на один уровень яркости попадает, в среднем, no = N ·M/J пикселов. Например, N = M = 512, J = 256. В этом случае no = 1024. Расстояние ∆fмежду дискретными уровнями яркости от fiдо fi+1в гистограмме исходного изображения одинаковое, но на каждый уровень выпадает различное число пикселов. При эквализации гистограммы расстояние ∆gi между уровнями gi и gi+1 различно, но число пикселов на каждом уровне, в среднем, одинаковое и равно no. Алгоритм эквализации несложен. Пусть уровнями с малой яркостью обладает небольшое количество пикселов, как на рис. 3а. Например, уровень яркости 0 на исходном изображении имеют 188 пикселов, уровень 1 - 347
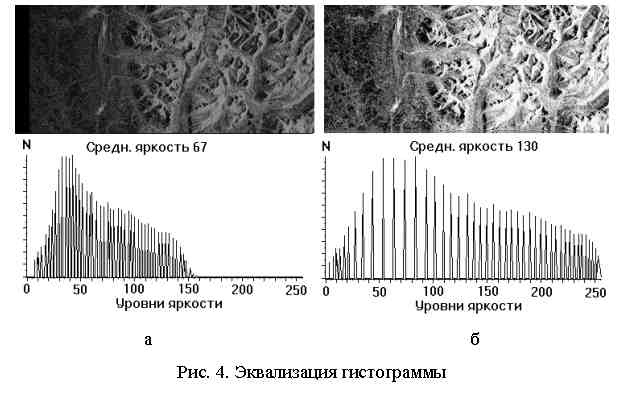
пикселов, уровень 2 - 544 пиксела. В сумме это 1079 пикселов, т.е. приблизительно no. Присвоим всем этим пикселам уровень 0. Пусть на исходном изображении число пикселов с уровнями яркости 3 и 4 в сумме приблизительно также равно no. Этим пикселам присваивается уровень 1. С другой стороны, пусть число пикселов с уровнем 45 на исходном изображении составляет 3012, т.е. приблизительно 3no. Всем этим пикселам присваивается некоторый одинаковый уровень gi, не обязательно равный 45, а соседние два уровня остаются незаполненными. Рассмотренные процедуры выполняются для всех уровней яркости. Результат эквализации можно видеть на рис. 4б. В каждом конкретном случае выбирают ту процедуру преобразования гистограмм, которая приводит к наилучшему, с точки зрения пользователя, результату.
3. Фильтрация изображений
Реальные изображения наряду с полезной информацией содержат различные помехи. Источниками помех являются собственные шумы фотоприемных устройств, зернистость фотоматериалов, шумы каналов связи. Наконец, возможны геометрические искажения, изображение может быть расфокусировано. Пусть f (x,y) – некоторое изображение, х, у – координаты.Реальное растровое изображение имеет конечные размеры: A ≤ x ≤ B, C ≤ y ≤ D и состоит из отдельных пикселов, расположенных с некоторым шагом в узлах прямоугольной сетки. Линейное преобразование изображения можно описать выражением
![]() (2)
(2)
Выражение (2), где интегрирование ведется по всей области определения x и y, характеризует преобразование всего изображения целиком - глобальную фильтрацию. Ядро преобразования h1 (x,y,x',y')в оптике именуют функцией рассеяния точки (ФРТ). Это изображение точечного источника на выходе оптической системы, которое уже является не точкой, а некоторым пятном. В соответствии с (2), все точки изображения f (x',y') превращаются в пятна, происходит суммирование (интегрирование) всех пятен. Не следует думать, что эта процедура обязательно приводит к расфокусировке изображения, наоборот, можно подобрать такую ФРТ, которая позволит сфокусировать расфокусированное изображение.
На рис. 5 представлена одна из возможных ФРТ. Вообще говоря, ФРТ определена на (- ∞ < x < ∞), (- ∞ < y < ∞). ФРТ не должна изменяться при изменении начала отсчета по x и y, для этого она должна иметь вид: h1(x,y,x',y')= =h1(x-x', y-y'). Кроме того, ФРТ должна обладать осевой симметрией. В этом случае все точки изображения "расплываются" одинаковым образом, равномерно во все стороны (принцип пространственной инвариантности).
 |
На практике глобальная фильтрация применяется редко. Чаще используют локальную фильтрацию, когда интегрирование и усреднение проводится не по всей области определения x и y, а по сравнительно небольшой окрестности каждой точки изображения. Функция рассеяния точки при этом имеет ограниченные размеры. Достоинством такого подхода является хорошее быстродействие. Линейное преобразование принимает вид:
![]() (3)
(3)
При обработке растровых изображений, которые состоят из отдельных пикселов, интегрирование заменено суммированием. Проще всего реализовать ФРТ конечных размеров в виде прямоугольной матрицы форматом N´N. N может быть равным 3, 5, 7 и т.д. Например, при N = 3
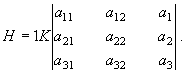
Суммирование ведется по окрестности D точки (i, j); akl - значения ФРТ в этой окрестности. Яркости пикселов f в этой точке и в её окрестности умножаются на коэффициенты akl, преобразованная яркость (i,j) -го пиксела есть сумма этих произведений. Элементы матрицы удовлетворяют условию пространственной инвариантности, поэтому a11= a13 =a31= a33, a12 = a21= a23 = a32. Только три элемента матрицы размером 3х3 независимы, в этом случае матрица инвариантна относительно поворотов, кратных 90˚. Опыт обработки изображений показывает, что отсутствие более строгой осевой симметрии ФРТ слабо сказывается на результатах. Иногда используют 8-угольные матрицы, инвариантные относительно поворотов на 45˚.
Фильтрация согласно (3) осуществляется перемещением слева направо (или сверху вниз) маски на один пиксел. При каждом положении апертуры производятся упомянутые выше операции, а именно перемножение весовых множителей akl с соответствующими значениями яркостей исходного изображения и суммированием произведений. Полученное значение присваивается центральному (i,j) -му пикселу. Обычно это значение делится на заранее заданное число K (нормирующий множитель). Маска содержит нечетное число строк и столбцов N, чтобы центральный элемент определялся однозначно.
Рассмотрим некоторые фильтры, сглаживающие шум. Пусть маска размером 3х3 имеет вид:

Тогда яркость (i,j) -го пиксела после фильтрации определится как
![]()
Хотя коэффициенты akl можно выбрать из среднеквадратического или иного условия близости не искаженного шумом si,j и преобразованного gi,j изображений, обычно их задают эвристически. Приведем еще некоторые матрицы шумоподавляющих фильтров:
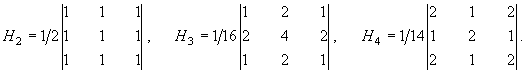
У фильтров H1 - H4 нормирующие множители K подобраны таким образом, чтобы не происходило изменения средней яркости обработанного изображения. Наряду с масками 3х3 используются маски большей размерности, например, 5х5, 7х7 и т.п. В отличие от фильтра H2, у фильтров H1, H3, H4 весовые коэффициенты на пересечении главных диагоналей матрицы больше, чем коэффициенты, стоящие на периферии. Фильтры H1, H3, H4 дают более плавное изменение яркости по изображению, чем H2.
Пусть отсчеты полезного изображения fk,m мало меняются в пределах маски. На изображение накладывается аддитивный шум: fk,m + nk,m , отсчеты шума nk,m случайны и независимы (или слабо зависимы) со статистической точки зрения. В этом случае механизм подавления шума с использованием приведенных фильтров состоит в том, при суммировании шумы компенсируют друг друга. Эта компенсация будет происходить тем успешнее, чем большее число членов в сумме, т.е. чем больше размер (апертура) маски. Пусть, например, используется маска N´N, в пределах её полезное изображение имеет постоянную яркость f, шум с независимыми значениями отсчетов nk,m, средним значением μ = 0 и дисперсией σ2 в пределах маски (такой шум называют белым). Отношение квадрата яркости (i,j)-го пиксела к дисперсии шума, т.е. отношение сигнал/шум, равно f 2/σ2.
Рассмотрим, например, маску типа H2:

Средний квадрат яркости равен f 2, средний квадрат интенсивности шума
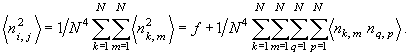
Двойная сумма отвечает k= p, m = q, эта сумма равна σ2/N 2.Четырехкратная сумма равна нулю, так как отсчеты шума при k ≠ p, m ≠ q независимы: <n k,mn p,q> = 0. В результате фильтрации отношение сигнал/шум становится равным N 2f 2/σ2, т.е. возрастает пропорционально площади маски. Отношение яркости (i,j)-го пиксела полезного изображения к среднеквадратическому отклонению шума возрастает пропорционально N. Применение маски 3х3, в среднем, повышает отношение сигнала к шуму в 9 раз.
При импульсной помехе механизм подавления состоит в том, что импульс "расплывается" и становится мало заметным на общем фоне.
Однако часто в пределах апертуры значения полезного изображения все же изменяются заметным образом. Это бывает, в частности, когда в пределы маски попадают контуры. С физической точки зрения, все H1 - H4 являются фильтрами нижних частот (усредняющими фильтрами), подавляющими высокочастотные гармоники и шума, и полезного изображения. Это приводит не только к ослаблению шума, но и к размыванию контуров на изображении. На рис. 6а показано исходное зашумленное изображение, результат применения фильтра типа Н2 приведен на рис. 6б (маска 5х5).
 |
![]()
Рассмотренная выше
фильтрация характеризовалась тем, что выходные значения фильтра
g определялись только через входные значения фильтра
f . Такие фильтры называются не рекурсивными. Фильтры,
в которых выходные значения g определяются не только через входные
значения f , но и через соответствующие выходные значения,
называются рекурсивными.
При рекурсивной фильтрации можно сохранять те же значения весовых множителей, что и приведенные выше, существуют рекурсивные фильтры со специально подобранными множителями. Элементы входного изображения в пределах окна изменятся и примут вид:
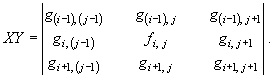
Весовые и нормирующий множители рекурсивного фильтра зависят от местоположения маски; рекурсивный локальный фильтр позволяет учитывать все входные значения фильтруемого изображения, т.е. приближается по своему действию к глобальному фильтру.
Для устранения эффекта размывания контуров при подавлении шума следует переходить к нелинейной обработке. Примером нелинейного фильтра для подавления шума служит медианный фильтр. При медианной фильтрации (i,j)-му пикселу присваивается медианное значение яркости, т.е. такое значение, частота которого равна 0,5. Пусть, например, используется маска 3´3, в пределы которой наряду с более или менее равномерным фоном попал шумовой выброс, этот выброс пришелся на центральный элемент маски:

Строится вариационный ряд. Вариационным рядом V1,..., Vn выборки f1,..., fn называют упорядоченную по не убыванию последовательность элементов выборки, т.е. V1 = min(f1,..., fn), Vn= max (f1,..., fn) и т.д. В нашем случае вариационный ряд имеет вид: 63, 66, 68, 71, 74, 79, 83, 89, 212. Здесь медианное значение - пятое по счету (подчеркнуто), так как всего чисел в ряду 9. При медианной фильтрации значение 212, искаженное шумовым выбросом, заменяется на 74, выброс на изображении полностью подавлен. Результат применения медианного фильтра показан на рис. 6в.
Функция рассеяния точки для медианного фильтра есть нуль. При размерах окна (2k+1)·(2k+1) происходит полное подавление помех, состоящих не более, чем из 2(k2 + k) пикселов, а также тех, которые пересекаются не более, с k строками или k столбцами, При этом не изменяется яркость в точках фона. Разумеется, при медианной фильтрации может происходить искажение объекта на изображении, но только на границе или вблизи нее, если размеры объекта больше размеров маски. Фильтр обладает высокой эффективностью при подавлении импульсных помех, однако это качество достигается подбором размеров маски, когда известны минимальные размеры объектов и максимальные размеры искаженных помехой локальных областей.
4. Выделение контуров
Линейные фильтры могут быть предназначены не для подавления шума, а для подчеркивания перепадов яркости и контуров. Выделение вертикальных перепадов осуществляется дифференцированием по строкам, горизонтальных - по столбцам. Дифференцирование производится в цифровой форме:

Здесь ∆x=1 - приращение вдоль строки, равное 1 пикселу, ∆y=1 - приращение вдоль столбца, также равное 1 пикселу. Выделение перепадов по диагонали можно получить, вычисляя разности уровней диагональных пар элементов.
Для выделения перепадов используются следующие наборы весовых множителей, реализующих двумерное дифференцирование:
север северо-восток восток юго-восток

юг юго-запад запад северо-запад
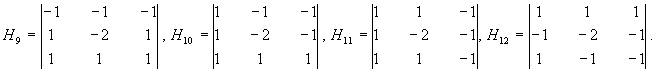
Название географических направлений говорит о направлении склона перепада, вызывающего максимальный отклик фильтра. Сумма весовых множителей масок равна нулю, поэтому на участках изображения с постоянной яркостью эти фильтры дают нулевой отклик.
Выделение горизонтального перепада можно выполнить также путем вычисления приращения разности яркостей пикселов вдоль строки, что равноценно вычислению второй производной по направлению (оператор Лапласа):
![]()
Это отвечает одномерной маске Н = | -1 2 -1|, сумма весовых множителей равна нулю. Таким же образом можно искать перепады по вертикали и по диагонали. Для выделения перепадов без учета их ориентации используются двумерные операторы Лапласа:
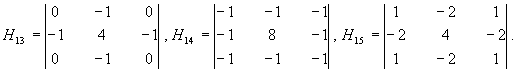
Здесь сумма весовых множителей также равна нулю. На рис. 7 приведено исходное изображение и результат применения оператора Лапласа Н13.
Операторы Лапласа реагируют на перепады яркости в виде ступенчатого перепада и на "крышеобразный" перепад. Они также выделяет изолированные точки, тонкие линии, их концы и острые углы объектов. Линия подчеркивается в 2 раза ярче, чем ступенчатый перепад, конец линии в 3 раза, а точка - в 4 раза ярче. Оператор Лапласа не инвариантен к ориентации перепадов: напри-
мер, отклик оператора на наклонный перепад в диагональном направлении почти вдвое больше, чем в горизонтальном и вертикальном.
С физической точки зрения, фильтры H5 - H15 являются фильтрами верхних частот, они выделяют высокочастотные составляющие полезного изображения, ответственные за перепады яркости и контуры и подавляют "постоянную составляющую". Однако при их использовании уровень шума на изображении возрастает.
Фильтры для выделения перепадов и границ, как и фильтры H1 - H4 для подавления шума, могут быть рекурсивными.
Изображение с подчеркнутыми границами (контурами) субъективно воспринимается лучше, чем оригинал. Происходит фокусировка частично расфокусированного изображения. При использовании оператора Лапласа для этих целей применяют три типовых набора весовых множителей:

H16 - H18 отличаются от фильтров H13 - H15 тем, что к центральному элементу матрицы прибавлена 1, т.е. при фильтрации исходное изображение накладывается на контур.
Для выделения контуров и перепадов яркости могут применяться нелинейные фильтры. В нелинейных алгоритмах используют нелинейные операторы дискретного дифференцирования. В фильтре Робертса используется перемещающаяся по изображению маска 2´2:
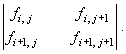
дифференцирования производится с помощью одного из выражений
![]()
![]()
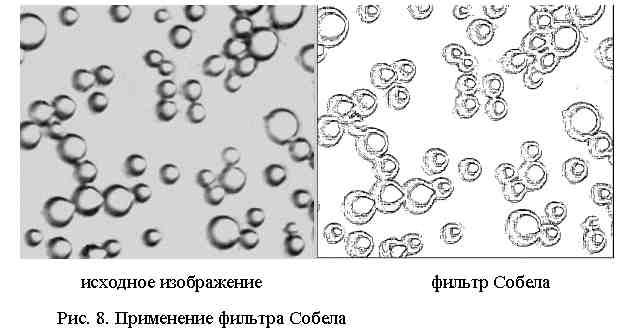 |
В фильтре Собела используется окно 3´3:

Центральному
(i,j) -му пикселу вместо f i,j
присваивается значение яркости ![]() либо
либо
![]() , где
, где

На рис. 8 показаны результаты применения фильтра Собела.
ЛИТЕРАТУРА
1. Агапов И.А., Кашкин В.Б. Обработка изображений: метод. указания, ч. 1,2//Красноярский гос.ун-т, Красноярск, 1994.
2. Кашкин В.Б. Цифровая обработка изображений. Дистанционное зондирование Земли из космоса//Метод. указания для студентов ФИВТ, КГТУ, Красноярск, 1998.
2. Бутаков Е.А., Островский В.И., Фадеев И.Л. Обработка изображений на ЭВМ. М., Радио и связь, 1987.
3.Мартинес Ф. Синтез изображений. М.: Радио и связь, 1990.
4.Павлидис Т.. Алгоритмы машинной графики и обработки изображений. М.: Радио и связь, 1986.
5.Прэтт У. Цифровая обработка изображений. М.: Мир, т.1,2. 1982.
6. Сойфер В.А. Компьютерная обработка изображений, Ч. 1//Соровский образовательный журнал, № 2, 1996, с. 118-124.
7. Сойфер В.А. Компьютерная обработка изображений Ч. 2//Соровский образовательный журнал, № 3, 1996 , c. 110-121.
8.Хорн Б.К.П. Зрение роботов. М.: Мир, 1989.
9. Техническое описание IBAS-2000.
10. Фролов Г.И., Бондаренко Г.В. Получение и исследование физических свойств пленок 3d-металлов, осажденных в условиях сверхбыстрой конденсации//Метод. указания к специальному практикуму по курсу «Физическое материаловедение», САА, Красноярск, 1998.