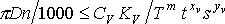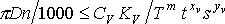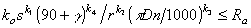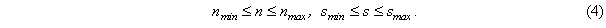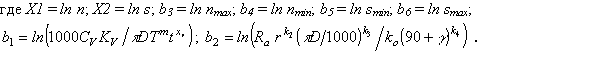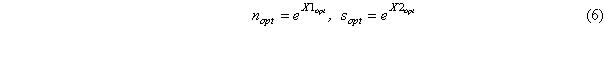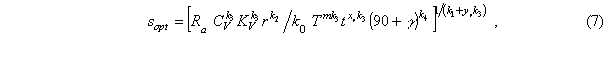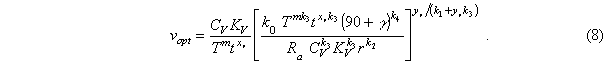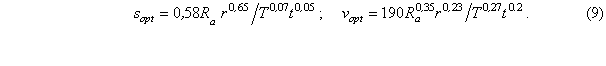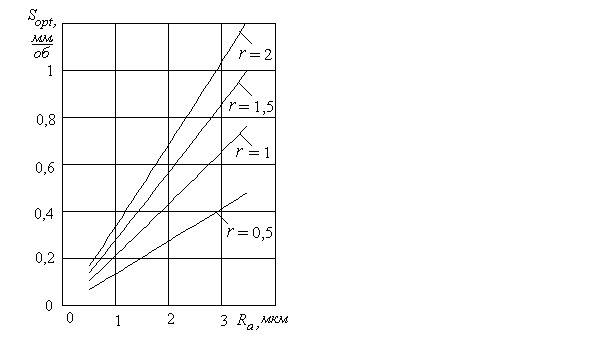Главная страница
Электронная библиотека
ВЫБОР ОПТИМАЛЬНЫХ РЕЖИМОВ РЕЗАНИЯ
ПРИ ЧИСТОВОЙ ТОКАРНОЙ ОБРАБОТКЕ
Самофалова М.А., Дубоделова О.М., Ивченко Т.Г.
(каф. ТМ, ДонНТУ, г.Донецк, Украина)
Обеспечение качества обработанной поверхности с достижением максимально возможной производительности механической обработки - важнейшая задача, решаемая при проектировании технологических процессов изготовления деталей. Одним из резервов повышения производительности является выбор рациональных параметров процесса резания. В связи с этим весьма актуальны исследования по определению оптимальных режимов резания, обеспечивающих для заданных условий обработки и требований к качеству обработанных поверхностей максимальную производительность.
Одним из наиболее распространенных методов оптимизации в настоящее время является метод линейного программирования [1], позволяющий осуществлять одновременную оптимизацию скорости резания и подачи с учетом действующих при реза-нии ограничений по критерию максимальной производительности. Для линейной целе-вой функции и линейных ограничений достаточно хорошо разработан и широко используется графический метод поиска оптимальных режимов резания. Несмотря на простоту и наглядность, этот метод не позволяет теоретически анализировать получаемые результаты в зависимости от условий обработки.
Цель представляемой работы - установить взаимосвязь оптимальных режимов резания с условиями механообработки и показателями качества обработанной поверхности при чистовой токарной обработке.
В качестве целевой функции рассматривается производительность обработки, определяемая основным временем:
t0=L/ns (1)
где L - длина обработки, n, s - частота вращения и подача.
Максимум производительности достигается при минимуме основного времени, или максимуме произведения n s max.
Для чистовой токарной обработки рассматриваются следующие основные ограничения:
- по режущим возможностям инструмента, определяемым скоростью резания, соответствующей его стойкости, учитывающей требования к периодичности смены инст-румента в связи с организационной формой обслуживания оборудования [2]:
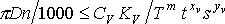
где D - диаметр обработки, CV, KV - коэффициенты и xv, yv, m - показатели, характеризующие степень влияния глубины t, подачи s и стойкости T на скорость резания v, оп-ределяемые в зависимости от условий эксплуатации;
- по предельно допустимой шероховатости обработанной поверхности Ra [3]:
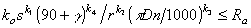
где k0, k1, k2, k3, k4 - коэффициент и показатели, характеризующие степень влияния по-дачи s, переднего угла , радиуса при вершине r и скорости v на шероховатость обрабо-танной поверхности Ra, определяемые в зависимости от условий эксплуатации;
- по предельно допустимым диапазонам частоты вращения и подачи, определяе-мым кинематической структурой привода главного движения и привода подач:
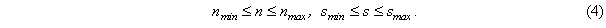
В результате линеаризации целевой функции и ограничений путем логарифмиро-вания получается следующая математическая модель процесса резания, выраженная системой линейных неравенств, графически представленных на рис.1:
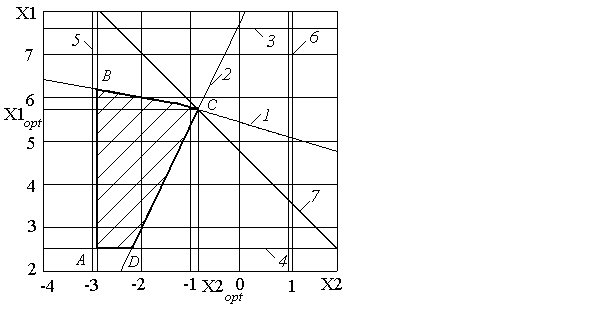
Рис. 1. Схема определения оптимальных режимов резания для чистовой обработки
(графики построены для следующих условий механической обработки:
D = 200 мм; CV =350; KV = 1; xv = 0,15; yv = 0,35; m = 0,2; t = 1мм; T = 60мин; = 0 ; r = 1мм; k0 = 7,0; k1 = 0,85; k2 = 0,65; k3 = 0,36; k4 = 0,15; Ra, = 1,25 мкм).

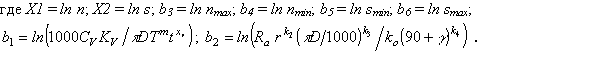
Многоугольник АВСД представляет собой область возможных решений. Целевая функция принимает максимальное значение в точке С, для которой сумма расстояний до осей (X1+X2) максимальна, о чем свидетельствует крайне возможное положение линии 7, характеризующей целевую функцию. Координаты точки С(X1оpt, X2оpt) являются искомыми оптимальными значениями параметров, на основании которых определяют-ся оптимальные частота вращения и подача:
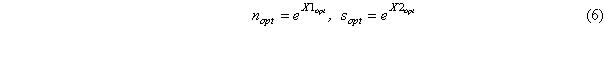
Представленный график наглядно иллюстрирует, что при чистовой обработке оптимальные значения режимов резания не зависят от кинематических ограничений, указанных на графике линиями 3, 4, 5, 6, а определяются только ограничениями по режущим способностям инструмента и шероховатости обработанной поверхности Ra, заданными линиями 1 и 2. В таком случае оптимальные подача и скорость резания могут быть определены аналитически:
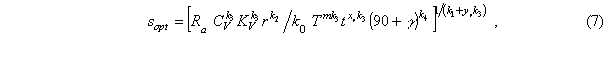
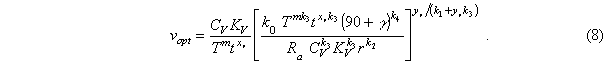
Для указанных ранее условий чистовой токарной обработки после подстановки постоянных параметров получены зависимости оптимальных значений подачи и скоро-сти резания от шероховатости обработанной поверхности Ra, радиуса при вершине r, стойкости Т и глубины резания t, позволяющие аналитически рассчитать оптимальные режимы обработки, обеспечивающие максимальную производительность:
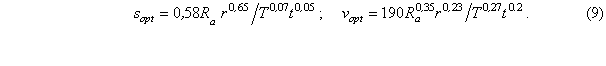
Графически зависимости оптимальных значений подачи sоpt от шероховатости обработанной поверхности Ra при различных значениях радиуса при вершине, представлены на рис.2.
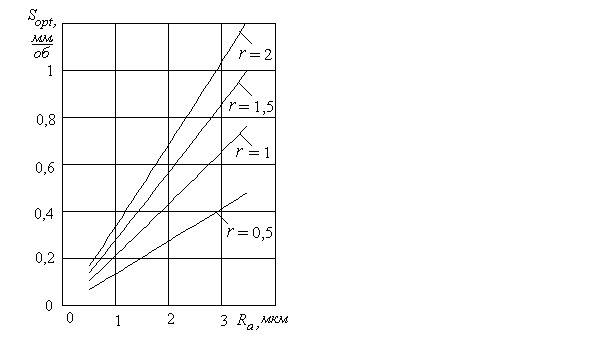
Рис. 2. Графики зависимости оптимальных значений подачи sоpt от шероховатости обработанной поверхности
В этом случае для расчетов использована следующая зависимость:

Таким образом, с использованием метода линейного программирования установлена взаимосвязь режимов резания с условиями механообработки и показателями качества обработанной поверхности при чистовой токарной обработке.
Для продольного наружного точения конструкционных сталей резцами, оснащенными твердыми сплавами, даны аналитические и графические зависимости оптимальных значений скорости резания и подачи от основных параметров механической обработки и шероховатости обработанной поверхности.
На основании полученных результатов могут быть разработаны рекомендации по выбору оптимальных режимов резания в любых условиях получистовой и чистовой токарной обработки различных обрабатываемых и инструментальных материалов.
Список литературы:
1. Старков В.К. Обработка резанием. Управление стабильно-стью и качеством в автоматизированном производстве. - М.: Машиностроение. 1989. - 296с.
2. Справочник технолога-машиностроителя. / Под ред. А.Г.Косиловой, Р.К.Мещерякова. В 2 т.- 4-е изд., перераб. и доп. - М.: Машиностроение, 1986, т.2. - 496с.
3. Суслов А.Г., Дальский А.М. Научные основы технологии машиностроения. М.: Машиностроение, 2002. - 84с.
Вверх
Электронная библиотека
Главная страница