И.И. Рашоян, аспирант
Самарский государственный технический университет


ANALISIS OF ABRASIVE GRAIN KINEMATICS IN PLUNGE-CUT CYLINDRICAL GRINDING

I.I. Rashoian, post-graduate student
Samara state technical university

The derivation of equations, determining the length of a curve of abrasive circle contact in various kinds of plunge-cut cylindrical grinding in terms of the lateral feed is, given in the paper.

Исследование кинематики абразивного зерна при различных способах шлифования является одним из вопросов теоретического анализа этого процесса. Основные уравнения, определяющие траекторию резания абразивным зерном, длину кривой контакта зерна с деталью необходимы для изучения условий взаимодействия шлифовального круга с обрабатываемой деталью и, прежде всего, для определения глубины внедрения абразивного зерна в материал детали. Глубина внедрения зерна (а_z) является важным фактором, который позволяет оценить нагрузку на шлифующее зерно, температуру в зоне резания, износ круга и определить пути целенаправленного регулирования режимов шлифования для достижения требуемых характеристик точности и качества обработки [ 1] .

Вопросы кинематического анализа процесса круглого врезного наружного и внутреннего шлифования рассмотрены во многих работах [ 2,3] . Однако, в них не учтены поперечная подача [ 2] и поворот осей системы координат, связанной с деталью [ 3] . Следует также отметить, что при круглом врезном шлифовании радиус детали является переменной величиной, которая изменятся в пределах от r_n (радиус детали до начала процесса шлифования) до r_k (радиус детали после шлифования) по зависимости:

r(t) = r_n ± V_n t, (1)

где V_n – поперечная подача, мм/мин, t – время шлифования, мин, знак “+” относится к внутреннему врезному шлифованию, знак “–” – к наружному. Следовательно, длина кривой контакта в процессе шлифования тоже будет непостоянной величиной.

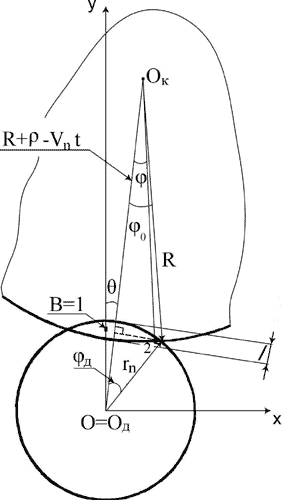
Для составления основных уравнений, определяющих траекторию движения абразивного зерна относительно детали, рассмотрим процесс наружного врезного шлифования (рис 1). Пусть шлифовальный круг радиусом R, мм, вращается против часовой стрелки с частотой n_k, об/мин, поступательно перемещаясь к центру детали со скоростью V_n, мм/мин, а обрабатываемая деталь вращается против часовой стрелки с частотой n_д, об/мин. Радиус детали в начале траектории резания (царапанья) некоторого зерна примем равным r = r_n - l, где l – глубина шлифования, мм.

Рисунок 1 – Схема для определения перемещений при круглом наружном шлифовании

Введем систему координат XOY, жестко связанную с центром вращения детали. Ось OY проходит через точку детали В, которую примем за начало контакта абразивного зерна с деталью (ОВ = О1 = r ). Через некоторое время t круг повернулся на угол j = 2·p·n_k·t, а деталь – на угол q  = 2·p·n_д·t. В системе координат, связанной с деталью, ось круга повернется относительно оси OY на угол q по часовой стрелке (встречное шлифование). Центр круга сместится вдоль своей оси к центру детали на величину V_n·t. Составим уравнения движения зерна круга из положения 1 (начало контакта) в положение 2:

X = (R + r – V_n·t)·sinq + R·sin(j – q)        

Y = (R + r – V_n·t)·cosq – R·cos(j – q)     (2)

Длина кривой контакта круга с деталью определится соотношением

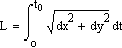   (3)

Продифференцируем уравнения (2), подставим их в формулу (3) и заменим переменную интегрирования, пользуясь соотношением

dt = dj /(2·p·n_k)    (4)

В результате получим:

L_нв =     (5)

Проинтегрировав и упростив выражение (5), будем иметь:

L_нв = 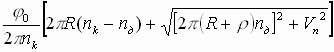    (6)

Угол контакта j ₀ определим из системы уравнений:

R·sin j_o = r_n·sin j_д

l = r_n – r_n·cos j_д + R – R·cos j_o    (7)

Решив систему (7), получим

j _o = 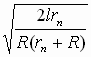    (8)

Подставим выражение (8) в (6) и получим формулу для определения длины кривой контакта шлифовального круга с обрабатываемой деталью при круглом наружном (встречном) шлифовании с поперечной подачей:

L_нв = 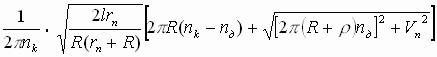    (9)

Аналогичным образом найдены формулы для других видов шлифования:

для наружного попутного:

L_нп = 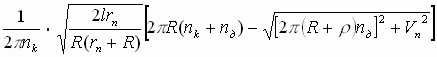   (10)

для внутреннего встречного:

L_вв = 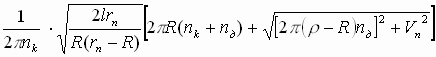   (11)

для внутреннего попутного:

L_вп = 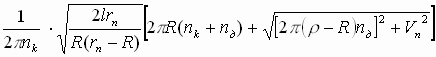   (12)

В результате кинематического анализа различных видов круглого врезного шлифования получены формулы (9 – 12), позволяющие с большей степенью точности определить как длину кривой контакта, так и глубину внедрения абразивного зерна в материал детали а_z [1] , которая влияет на силу резания единичным абразивным зерном, температуру в зоне контакта, а следовательно, и на качество шлифованной поверхности.

СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ

1. Рашоян И.И. Анализ процесса микрорезания при круглом врезном шлифовании // Фундаментальные и прикладные проблемы технологии машиностроения. Сб. науч. трудов МДНТК “Технология – 2001”, Орел, 2001.
2. Маслов Е.Н. Теория шлифования металлов. М., Машиностроение, 1974.
3. Евсеев Д.Г., Сальников А.Н. Физические основы процесса шлифования. Саратов, изд-во Саратовского университета, 1978.