На револьверном станке обрабатывается 300 шт валиков из стали 45. Диаметр заготовок d = 25 мм, длина l = 40 мм. Допуск на обработку Т = 0,1 мм. Материал резца Т30К4. Режим резания: V = 150 м/мин; подача S = 0,08 мм/об; t = 0,5 мм. Относительный износ резца при указаных режимах составляет u₀ = 0,5 мкм/км.
По пробной партии экспериментально установлено и подсчитано, что рассеяние размеров при обработке на данном станке характеризуется средним квадратичным отклонением s = 0,025 мм.
Определить количество годных и бракованных деталей при условии, что настройка станка обеспечивает симметричное расположение кривой расеяния относительно середины поля допуска.


Oтвет:

В связи с тем, что за счет износа резца при обработке 300 шт заготовок происходит непрерывное смещение вершины кривой расеяния Гаусса вправо (в сторону увеличения размеров), считаем, что фактическое распределение размеров подчиняется функции a(t), и по условиям задачи соответствует схеме, изображенной на рисунке.

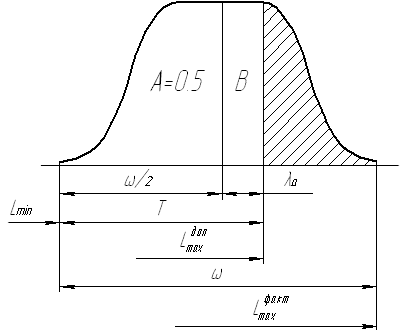
Смещение центра группирования 2l кривой определяется увеличением диаметра обработанных заготовок за счет износа резца в период обработки, то есть 2l = 2u, где u = u₀(L + L_доб)/1000. Путь резания L при обработке n = 300 шт заготовок равен:

L = p·D·l·n/(1000·S) = 3,14·25·40·300/(1000·0,08) = 11775 м;

износ:

u = 0,0065·(11775 + 1000)/1000 = 0,083 мм;

l = u = 0,083 мм.
смещение центра группирования 2l = 0,166 мм.

oпределим параметр l_a :


среднее квадратичное отклонение функции a(t):



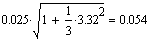
для определения количества вероятного брака, вычисляется значение t_a:


количество годных деталей при l_a = 3,0 и t_a = 0,926 согласно табличным данным равно:

Q = 2·Ф(t_a,l_a) = 2·0,2969 = 0,5938 = 59,38%
то есть 178 шт, брак – 40,62% или 122 шт.