| |
УДК 621.311.153.001.24
СТАТИСТИЧЕСКИЕ РЕШЕНИЯ НЕЛИНЕЙНЫХ ЗАДАЧ ТЕОРИИ ЭЛЕКТРИЧЕСКИХ НАГРУЗОК СЕТЕЙ ЭЛЕКТРОСНАБЖЕНИЯ ПРОМЫШЛЕННЫХ ПРЕДПРИЯТИЙ
Погребняк Н.Н.
Донецкий государственный технический университет
The application of a method of least squares for calculation of a parameter of exponential correlation function of the group random power load is suggested. The results of a statistical finding of a problem about inertial smoothing of quadrate of a casual electrical load are analysed. The engineering methods of determination of electrical loads are substantiated. The results of testing of existing and offered engineering methods of calculation of loads of industrial electrical networks are demonstrated.
В теории электрических нагрузок и при оценке электромагнитной совместимости электроприемников (ЭП) определяются воздействия случайной нагрузки или напряжения на сеть и ЭП, которые зависят от потерь мощности и инерционности объектов. Поэтому в соответствующие математические модели входят квадратор и инерционное звено. Требуется определить характеристики случайного процесса после инерционного сглаживания квадрата входного процесса (квадратичного инерционного сглаживания). Задача имеет аналитическое решение только в частных случаях , в связи с чем необходимо применить метод статистического моделирования (имитационный метод).
В качестве примера нелинейной задачи рассмотрим определение расчетной электрической нагрузки по нагреву проводника, питающего группу ЭП. От правильности расчета нагрузок зависят техническая и экономическая эффективность системы электроснабжения промышленного предприятия, а из-за отсутствия аналитического решения при создании инженерных методов использовались допущения, не обеспечивающие требуемую точность (  10%). Для уменьшения погрешности необходимо найти статистическое решение задачи о квадратичном инерционном сглаживании для характерных графиков групповой нагрузки и на его основе предложить более точные инженерные методы расчета. 10%). Для уменьшения погрешности необходимо найти статистическое решение задачи о квадратичном инерционном сглаживании для характерных графиков групповой нагрузки и на его основе предложить более точные инженерные методы расчета.
В теории электрических нагрузок принята обоснованная профессором Г.М. Каяловым простая модель нагрева проводника с постоянной времени нагрева 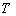 при протекании по нему тока нагрузки при протекании по нему тока нагрузки 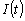 в виде уравнения в виде уравнения
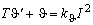 ,(1) ,(1)
где  - температура перегрева проводника; - температура перегрева проводника;  (для трехжильного кабеля); (для трехжильного кабеля); 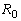 - активное сопротивление жилы проводника при температуре 20°С; - активное сопротивление жилы проводника при температуре 20°С; - коэффициент теплоотдачи. - коэффициент теплоотдачи.
Для пропорциональной температуре перегрева величины 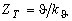 введем термин "греющая доза", которая измеряется в А2. введем термин "греющая доза", которая измеряется в А2.
В существующей проектной практике принято раздельное определение активной и реактивной нагрузок 8]. На данном этапе такой подход будет сохранен, хотя, строго говоря, необходимо одновременно имитировать активную и реактивную нагрузки, учитывая вероятностную связь между ними. Далее будут рассматриваться методы определения активной расчетной нагрузки, а для реактивной будет практически сохранен существующий способ расчета.
График активной нагрузки каждого ЭП с номинальной мощностью  , средней длительностью цикла , средней длительностью цикла  , коэффициентом загрузки , коэффициентом загрузки 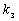 , коэффициентом , коэффициентом 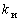 использования может быть представлен состоящим из двух ступеней: импульса величиной использования может быть представлен состоящим из двух ступеней: импульса величиной 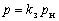 продолжительностью продолжительностью 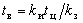 и нулевой паузы длительностью и нулевой паузы длительностью 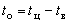 . В реальных условиях ЭП работают с некоторой, но не строгой периодичностью, поэтому корреляционная функция (КФ) индивидуальной нагрузки может быть аппроксимирована выражением . В реальных условиях ЭП работают с некоторой, но не строгой периодичностью, поэтому корреляционная функция (КФ) индивидуальной нагрузки может быть аппроксимирована выражением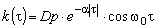 , (2) , (2)
где  - дисперсия индивидуальной нагрузки; - дисперсия индивидуальной нагрузки; 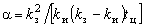 и и 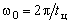 - параметры КФ. Результаты исследований КФ индивидуальных графиков активной нагрузки в действующих системах электроснабжения подтверждают, что для индивидуальных графиков, в основном, характерна экспоненциально-косинусоидальная КФ (2). - параметры КФ. Результаты исследований КФ индивидуальных графиков активной нагрузки в действующих системах электроснабжения подтверждают, что для индивидуальных графиков, в основном, характерна экспоненциально-косинусоидальная КФ (2).
При принятой модели индивидуальной нагрузки закон вероятностного распределения группового графика нагрузки определяется по теореме о повторении опытов . Такой закон распределения условно будем называть "комбинаторным". С ростом количества  ЭП, формирующих групповой график, его закон распределения в соответствии с центральной предельной теоремой теории вероятностей будет приближаться к нормальному. КФ группового графика нагрузки при небольшом числе ЭП сохраняет периодичность и аппроксимируется выражением (2). При большом количестве ЭП КФ группового графика периодичность не присуща, что объясняется различием в длительностях циклов отдельных ЭП и другими случайными факторами, поэтому в теории электрических нагрузок используется модель с экспоненциальной КФ ЭП, формирующих групповой график, его закон распределения в соответствии с центральной предельной теоремой теории вероятностей будет приближаться к нормальному. КФ группового графика нагрузки при небольшом числе ЭП сохраняет периодичность и аппроксимируется выражением (2). При большом количестве ЭП КФ группового графика периодичность не присуща, что объясняется различием в длительностях циклов отдельных ЭП и другими случайными факторами, поэтому в теории электрических нагрузок используется модель с экспоненциальной КФ  , (3) , (3)
где  - дисперсия группового графика нагрузки; - дисперсия группового графика нагрузки;  - эквивалентный параметр КФ. - эквивалентный параметр КФ.
Для имитации группового графика необходимо найти эквивалентный параметр ее КФ по известным параметрам КФ индивидуальных нагрузок. С этой целью в предложен метод эквивалентных площадей, а в рекомендован расчет  по инерционной дисперсии. по инерционной дисперсии.
Для определения  используем метод наименьших квадратов. В этом случае необходимо найти такое значение используем метод наименьших квадратов. В этом случае необходимо найти такое значение  , при котором функция , при котором функция
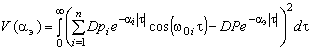 (4) (4)
достигает минимального значения, т.е. выполняется условие
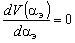 . (5) . (5)
После подстановки (4) в (5) и выполнения дифференцирования и интегрирования получаем трансцендентное уравнение для определения
 . (6) . (6)
Эквивалентный параметр КФ также можно рассчитать по времени корреляции:
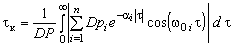 , ,  . (7) . (7)
Сопоставление известного метода эквивалентных площадей и предлагаемых способов расчета показало, что наименьшая погрешность определения дисперсии греющей дозы обеспечивается при применении метода наименьших квадратов. Приемлемую погрешность дает и эквивалентирование по инерционной дисперсии . Поэтому первый метод рекомендуется для выполнения расчетов на ЭВМ в связи с большим объемом вычислений при решении уравнения (6), а второй - для расчетов вручную.
Алгоритм применения метода статистического моделирования для определения расчетной нагрузки включает в себя следующие этапы: имитация ансамбля реализаций стационарного группового графика тока нагрузки 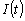 или активной мощности или активной мощности 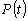 ; расчет ансамбля реализаций греющей дозы ; расчет ансамбля реализаций греющей дозы 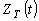 ; расчет статистической функции распределения греющей дозы по сечению полученного ансамбля ; расчет статистической функции распределения греющей дозы по сечению полученного ансамбля 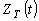 , после затухания переходного процесса нагрева проводника; определение максимального расчетного значения греющей дозы , после затухания переходного процесса нагрева проводника; определение максимального расчетного значения греющей дозы 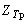 или или 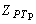 с заданной вероятностью с заданной вероятностью 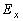 ее превышения - в соответствии с принципом практической уверенности; определение расчетной нагрузки по ее превышения - в соответствии с принципом практической уверенности; определение расчетной нагрузки по  току или по активной мощности току или по активной мощности 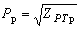 . .
Корректность имитационного метода подтверждается выполненной проверкой для случаев, когда аналитическое решение известно .
Имитационным методом решена задача квадратичного инерционного сглаживания для более чем 40 групповых графиков нагрузки с различными средними 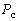 и эффективными и эффективными 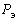 значениями, соотношение между которыми определяется коэффициентом формы значениями, соотношение между которыми определяется коэффициентом формы  , а также законами распределения ординат. Анализ накопленного статистического материала показал: , а также законами распределения ординат. Анализ накопленного статистического материала показал:
- для групповых графиков электрической нагрузки с 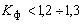 и комбинаторным распределением ординат возможна замена реального графика нагрузки моделью с нормальным распределением ординат и фактическими средним значением и КФ. При этом погрешность определения расчетной нагрузки не превышает допустимую при любом значении и комбинаторным распределением ординат возможна замена реального графика нагрузки моделью с нормальным распределением ординат и фактическими средним значением и КФ. При этом погрешность определения расчетной нагрузки не превышает допустимую при любом значении 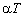 , а в диапазоне возможных на практике значений постоянной времени нагрева - не превышает 3,5%; , а в диапазоне возможных на практике значений постоянной времени нагрева - не превышает 3,5%;
- стандарт 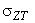 греющей дозы групповых графиков с комбинаторным и нормальным распределениями при отличаются незначительно. В этих случаях предложено дисперсию греющей дозы групповой нагрузки с комбинаторным распределением приближенно определять по известной формуле для нормально распределенной нагрузки с экспоненциальной КФ греющей дозы групповых графиков с комбинаторным и нормальным распределениями при отличаются незначительно. В этих случаях предложено дисперсию греющей дозы групповой нагрузки с комбинаторным распределением приближенно определять по известной формуле для нормально распределенной нагрузки с экспоненциальной КФ
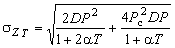 . (8) . (8)
Для комбинаторно распределенной групповой нагрузки с бoльшими значениями коэффициента формы формула (8) дает большую погрешность: например, при 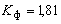 стандарт отличается в стандарт отличается в  раза; раза;
- величина статистического коэффициента 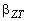 греющей дозы в диапазоне возможных на практике значений постоянной времени нагрева проводника почти не зависит от закона распределения и коэффициента формы группового графика нагрузки и находится в диапазоне от 1,76 до 1,97; греющей дозы в диапазоне возможных на практике значений постоянной времени нагрева проводника почти не зависит от закона распределения и коэффициента формы группового графика нагрузки и находится в диапазоне от 1,76 до 1,97;
- асимметрия и эксцесс греющей дозы с ростом 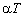 уменьшается, но и при достаточно больших значениях уменьшается, но и при достаточно больших значениях 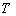 они отличны от нуля, следовательно, закон распределения греющей дозы не является нормальным; они отличны от нуля, следовательно, закон распределения греющей дозы не является нормальным;
- проверка по критерию Пирсона показала, что нормализация происходит при очень больших 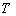 , но при этом дисперсия греющей дозы мало отличается от нуля, так что эти случаи не имеют практического значения. Если же исходить из допустимой погрешности расчета нагрузки , но при этом дисперсия греющей дозы мало отличается от нуля, так что эти случаи не имеют практического значения. Если же исходить из допустимой погрешности расчета нагрузки  10%, то допущение о нормальном распределении доз может быть принято, хотя расчетная нагрузка занижается. 10%, то допущение о нормальном распределении доз может быть принято, хотя расчетная нагрузка занижается.
В основу предлагаемых инженерных методов греющих доз (ГД) и уточненного метода греющих доз (УГД) положена общая формула для расчетного значения греющей дозы
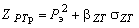 . (9) . (9)
Согласно методу ГД стандарт греющей дозы предлагается определять по формуле (8) для нормально распределенной групповой нагрузки. Различие между фактическим значением стандарта и определенным согласно (8) для групповой нагрузки с комбинаторным законом распределения ординат учитывается заменой статистического коэффициента 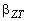 найденным из полученных статистических зависимостей коэффициентом найденным из полученных статистических зависимостей коэффициентом
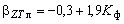 , (10) , (10)
равным произведению и корректирующего стандарт греющей дозы множителя, зависящего от коэффициента формы.
В уточненном методе греющих доз (УГД) для определения дисперсии греющей дозы предлагается использовать ее значение 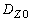 при при 
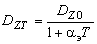 , (11) , (11)
а статистический коэффициент принимать равным 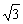 . Это значение и формула (11) также обоснованы имитационным методом. . Это значение и формула (11) также обоснованы имитационным методом.
При тестировании существующих и разработанных инженерных методов, в том числе и предложенного в уточненного инерционного метода, оценивалась их погрешность относительно определенной имитационным методом расчетной нагрузки для более чем 100 групповых графиков нагрузки. Полученные результаты представлены в виде диаграммы погрешностей 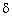 сопоставляемых методов на рис. 1. Методы УГД и ГД обеспечивают наибольшую точность, диапазоны их погрешностей симметричны относительно нуля, что говорит об отсутствии систематической погрешности, как, например, при применении методов упорядоченных диаграмм (УД) - в сторону завышения, а инерционного метода (ИМ) - в сторону занижения. Поэтому в качестве инженерных рекомендованы методы УГД - при расчетах на ЭВМ, ГД - для выполнения ориентировочных расчетов без применения ЭВМ. сопоставляемых методов на рис. 1. Методы УГД и ГД обеспечивают наибольшую точность, диапазоны их погрешностей симметричны относительно нуля, что говорит об отсутствии систематической погрешности, как, например, при применении методов упорядоченных диаграмм (УД) - в сторону завышения, а инерционного метода (ИМ) - в сторону занижения. Поэтому в качестве инженерных рекомендованы методы УГД - при расчетах на ЭВМ, ГД - для выполнения ориентировочных расчетов без применения ЭВМ.
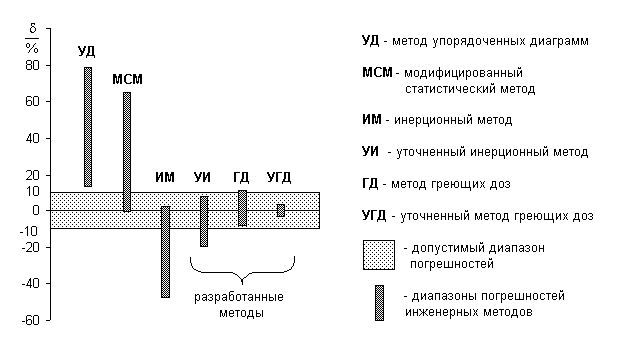
Рисунок 1 - Диапазоны погрешностей инженерных методов расчета электрических нагрузок
Выводы.
1. Расчет эквивалентного параметра КФ групповой нагрузки в формуле (3) рекомендуется выполнять согласно методу наименьших квадратов (при расчете на ЭВМ) или исходя из равенства инерционных дисперсий (при расчете вручную).
2. Имитационный метод эффективен при решении задач, не имеющих аналитического решения, и может применяться как самостоятельный при определении расчетных электрических нагрузок.
3. Закономерности, выявленные путем анализа статистического материала, объединяющего решение задачи о квадратичном инерционном сглаживании, позволили обосновать инженерные методы расчета электрических нагрузок промышленных предприятий. Разработанные методы ГД и УГД, как более точные по сравнению с существующими, рекомендуется для применения в проектной практике.
|
|

