| |
УДК[621.31.031.016.3:061.5].001.24
СОВЕРШЕНСТВОВАНИЕ МЕТОДОВ РАСЧЕТА ЭЛЕКТРИЧЕСКИХ НАГРУЗОК
Куренный Э.Г., Дмитриева Е.Н., Погребняк Н.Н.(ДонГТУ, г. Донецк),
Башков В.М.Киевпромэлектропроект, г. Киев)
В основу действующих Указаний [1] положен метод упорядоченных диаграмм (УД), предложенный профессором Г.М. Каяловым [2,3]. Метод сыграл значительную роль в становлении теории нагрузок и практики расчетов. Однако стремление к уменьшению объема исходной информации с целью упрощения расчетов обусловило принципиальную неточность метода УД. В статье рассматриваются методы расчета, которые могут быть использованы для разработки новых Указаний по определению электрических нагрузок.
При этом раскрывается физический смысл предлагаемых методов, но не сама методика практических расчетов (исходные справочные данные, расчетные кривые, примеры расчетов, программа вычислений на ЭВМ).
Понятие расчетной нагрузки. В [4] для каждого проводника нормируется длительно допустимый ток 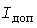 , которому соответствует допустимая температура , которому соответствует допустимая температура  проводника. Для возможности применения этих норм при изменяющейся нагрузке проводника. Для возможности применения этих норм при изменяющейся нагрузке 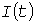 вводится понятие расчетной электрической вводится понятие расчетной электрической 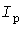 по нагреву - путем замены по нагреву - путем замены 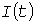 неизменной нагрузкой, которая вызывает те же тепловые эффекты. Обычно эквивалентирование выполняется из условия совпадения максимальной температуры неизменной нагрузкой, которая вызывает те же тепловые эффекты. Обычно эквивалентирование выполняется из условия совпадения максимальной температуры 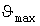 перегрева. Это дает запас по тепловому износу изоляции, который может быть оценен методом имитации. Однако практика проектирования пока не требует перехода к расчетной нагрузке по тепловому износу. перегрева. Это дает запас по тепловому износу изоляции, который может быть оценен методом имитации. Однако практика проектирования пока не требует перехода к расчетной нагрузке по тепловому износу.
В теории электрических нагрузок используется упрощенная тепловая модель проводника с постоянной времени  нагрева в виде инерционного звена, которое осуществляет «инерционное» преобразование нагрева в виде инерционного звена, которое осуществляет «инерционное» преобразование
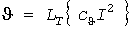
входного процесса  в процесс в процесс 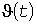 изменения температуры перегрева проводника, где изменения температуры перегрева проводника, где 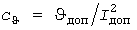 - коэффициент передачи звена в град./А2 (рис. 1, а). Инерционное преобразование эквивалентно решению дифференциального уравнения - коэффициент передачи звена в град./А2 (рис. 1, а). Инерционное преобразование эквивалентно решению дифференциального уравнения
 . (1) . (1)
Так как нормируется не температура, а нагрузка, то целесообразно перейти от  к «тепловой» нагрузке к «тепловой» нагрузке 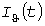 в амперах из условия в амперах из условия  . Для этого достаточно квадрат тока пропустить через инерционное звено, а из процесса . Для этого достаточно квадрат тока пропустить через инерционное звено, а из процесса 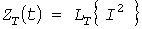 в А2 извлечь квадратный корень (рис. 1,б). Средняя температура в А2 извлечь квадратный корень (рис. 1,б). Средняя температура  пропорциональна квадрату эффективной нагрузки пропорциональна квадрату эффективной нагрузки  , а среднее значение квадрата тепловой нагрузки равно , а среднее значение квадрата тепловой нагрузки равно 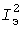 . В системе относительных единиц (о.е., символ *) с базовыми величинами . В системе относительных единиц (о.е., символ *) с базовыми величинами  и и 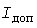 справедливы соотношения: справедливы соотношения:
 , , 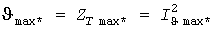  . .
Таким образом, по физическому смыслу в качестве расчетной нагрузки по нагреву следует принимать «инерционный»  -минутный тепловой максимум -минутный тепловой максимум
 . (2) . (2)
Принятое же в [4] понятие «кумулятивного» максимума получасовых средних нагрузок не отражает процесс нагрева, так как тридцатиминутное осреднение принципиально отличается от (1). Наиболее наглядно некорректность этого понятия проявляется в случае периодического графика любой конфигурации, длительность  цикла которого целое число раз укладывается на интервале 30 мин. Здесь получасовый «максимум» равен средней нагрузке цикла которого целое число раз укладывается на интервале 30 мин. Здесь получасовый «максимум» равен средней нагрузке 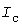 , хотя , хотя 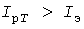 , а тем более , а тем более  . .
В тех случаях, когда эффективная и средняя нагрузки близки, расчетная нагрузка приближенно может быть определена как максимум 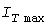 инерционного процесса инерционного процесса 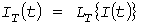 , который получается пропусканием нагрузки через инерционное звено (рис.1, в). Погрешность выражения , который получается пропусканием нагрузки через инерционное звено (рис.1, в). Погрешность выражения
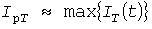 (3) (3)
не превышает величины
 . .
При допустимой погрешности 10% инерционные максимумы можно использовать при 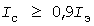 . .
В проектировании расчет ведется раздельно по активным 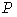 и реактивным и реактивным 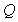 мощностям. Целью является получение расчетной нагрузки мощностям. Целью является получение расчетной нагрузки 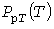 . Графики реактивной мощности более равномерны, поэтому по некоторой аналогии с действующими Указаниями далее для любых . Графики реактивной мощности более равномерны, поэтому по некоторой аналогии с действующими Указаниями далее для любых  принято принято  при при 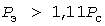 и и 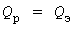 - в противном случае. - в противном случае.
В силу случайности процессов нагрузки и температуры расчетная нагрузка должна определяться с заданной вероятностью  ее превышения (в [5] принято ее превышения (в [5] принято  =0,05), что позволяет избежать завышения капиталовложений на сеть электроснабжения, так как расчетный максимум =0,05), что позволяет избежать завышения капиталовложений на сеть электроснабжения, так как расчетный максимум 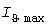 тепловой нагрузки меньше наибольшего значения тепловой нагрузки меньше наибольшего значения 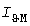 (при (при  =0). =0).
Характеристики нагрузки. График нагрузки электроприемника с номинальной мощностью 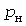 будем характеризовать средней мощностью и стандартом (средним квадратическим отклонением) будем характеризовать средней мощностью и стандартом (средним квадратическим отклонением) 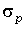 и соответствующими им коэффициентами и соответствующими им коэффициентами  использования и использования и 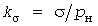 отклонений. отклонений.
Графики нагрузки электроприемника массового типа обычно представляют в виде последовательности прямоугольных импульсов величиной 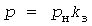 и нулевых пауз, где и нулевых пауз, где 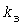 - коэффициент загрузки. Независимо от длительностей - коэффициент загрузки. Независимо от длительностей 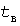 импульсов, импульсов, 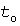 пауз и пауз и  циклов справедливы следующие выражения: циклов справедливы следующие выражения:
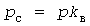 , , 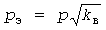 , , 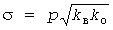 , (4) , (4)
 , , 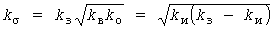 , ,
где 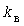 и и  - коэффициенты включения и отключения. - коэффициенты включения и отключения.
При одной и той же интенсивности  и коэффициенте включения, нагрев зависит от вероятностных распределений длительностей. Предельными являются два случая: периодическая последовательность импульсов отвечает режиму наибольшей проектной производительности, а нагрузка с экспоненциальными вероятностными распределениями длительностей импульсов и пауз - режиму с наибольшим перегревом проводника. Для группы и коэффициенте включения, нагрев зависит от вероятностных распределений длительностей. Предельными являются два случая: периодическая последовательность импульсов отвечает режиму наибольшей проектной производительности, а нагрузка с экспоненциальными вероятностными распределениями длительностей импульсов и пауз - режиму с наибольшим перегревом проводника. Для группы 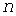 независимых приемников суммируются средние нагрузки и квадраты стандартов (дисперсии): независимых приемников суммируются средние нагрузки и квадраты стандартов (дисперсии):
 , (5) , (5)
 . (6) . (6)
Эффективная нагрузка и коэффициент формы вычисляются по формулам
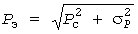 , , 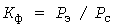 . (7) . (7)
Исчерпывающей характеристикой случайной величины  является вероятностное распределение, одной из форм представления которого является УД, построенная за время является вероятностное распределение, одной из форм представления которого является УД, построенная за время 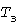 записи графика нагрузки, и для периодических процессов - за длительность цикла. Ординате записи графика нагрузки, и для периодических процессов - за длительность цикла. Ординате 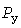 УД соответствует абсцисса УД соответствует абсцисса  , равная суммарной длительности выбросов нагрузки за уровень , равная суммарной длительности выбросов нагрузки за уровень 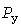 . В относительных единицах абсцисса . В относительных единицах абсцисса 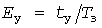 дает вероятность выбросов. дает вероятность выбросов.
Суммирование графиков с прямоугольными импульсами дает ступенчатый график нагрузки и ступенчатую УД. Если в некоторый момент времени включенными оказались 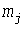 электроприемников с электроприемников с 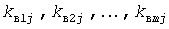 и и 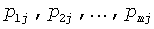 , то вероятность появления на графике , то вероятность появления на графике  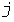 -й ступени величиной -й ступени величиной 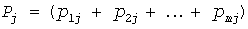 составит [6] составит [6]
 . (8) . (8)
Перебором всех возможных комбинаций получают пары значений 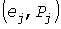 , по которым строится УД , по которым строится УД  мощностей в порядке возрастания мощностей в порядке возрастания 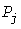 (рис. 3, сплошные линии): начальная ступенька нулевой величины имеет относительную длительность (рис. 3, сплошные линии): начальная ступенька нулевой величины имеет относительную длительность 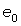 , равную произведению всех коэффициентов отключения, а конечная имеет величину , равную произведению всех коэффициентов отключения, а конечная имеет величину 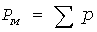 и относительную длительность и относительную длительность 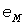 в виде произведения всех коэффициентов включения (светлые кружки). Для прямолинейности УД необходимо, чтобы при любом в виде произведения всех коэффициентов включения (светлые кружки). Для прямолинейности УД необходимо, чтобы при любом  разность разность 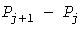 и вероятности (8) были бы постоянными. Первое условие выполняется для электроприемников с одинаковыми и вероятности (8) были бы постоянными. Первое условие выполняется для электроприемников с одинаковыми  , но второе - невыполнимо. , но второе - невыполнимо.
Отложив абсциссу 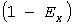 , найдем расчетный максимум , найдем расчетный максимум 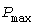 (темный кружок). Рис.3 и последующие рисунки построены для группы 5 электроприемников с номинальными мощностями 10, 15, 25, 30, 35 кВт, коэффициентами использования 0,2, 0,3 , 0,5 , 0,4 , 0,1 , с одинаковыми коэффициентами загрузки 0,8 и длительностями циклов 10 мин. Для этого Примера: (темный кружок). Рис.3 и последующие рисунки построены для группы 5 электроприемников с номинальными мощностями 10, 15, 25, 30, 35 кВт, коэффициентами использования 0,2, 0,3 , 0,5 , 0,4 , 0,1 , с одинаковыми коэффициентами загрузки 0,8 и длительностями циклов 10 мин. Для этого Примера: 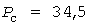 кВт, кВт,  кВт, кВт,  , , 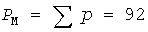 кВт, наименьшая нагрузка равна нулю, при кВт, наименьшая нагрузка равна нулю, при 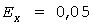 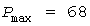 кВт. кВт.
По парам значений  может быть построена УД может быть построена УД 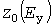 квадратов мощностей, совпадающая с УД процесса квадратов мощностей, совпадающая с УД процесса 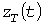 при при 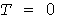 . Начальная и конечная ступеньки УД имеют координаты . Начальная и конечная ступеньки УД имеют координаты  и и  . Среднее значение квадратов нагрузки равно . Среднее значение квадратов нагрузки равно 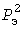 . По УД вычисляются стандарт . По УД вычисляются стандарт 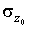 квадратов нагрузок, а для абсциссы квадратов нагрузок, а для абсциссы 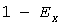 находится расчетное значение находится расчетное значение 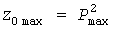 и определяется используемый в дальнейшем статистический коэффициент и определяется используемый в дальнейшем статистический коэффициент
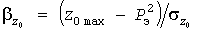 . (9) . (9)
Для Примера:  кВт2 кВт2 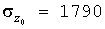 кВт2 , кВт2 , 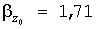 . .
Для оценки нагрева знания УД нагрузки недостаточно, поскольку тепловая нагрузка зависит от расположения ординат случайного процесса 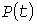 : даже возрастающая УД дает больший перегрев, чем убывающая. Линейную связь между ординатами : даже возрастающая УД дает больший перегрев, чем убывающая. Линейную связь между ординатами 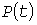 и и 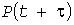 , разделенными интервалом , разделенными интервалом 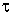 , в среднем характеризует корреляционная функция (КФ) , в среднем характеризует корреляционная функция (КФ) 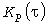 . .
Для группы массовых электроприемников в теории электрических нагрузок [3, 7] принимают экспоненциальную КФ
>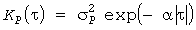 (10) (10)
с параметром 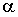 , обратным времени корреляции. , обратным времени корреляции.
Недостатки действующих указаний. В методе УД приняты два основные упрощающие допущения: во-первых, вместо графика 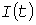 нагрузки используется его УД, периодически повторяющаяся с длительностью цикла нагрузки используется его УД, периодически повторяющаяся с длительностью цикла 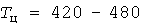 мин; во-вторых, УД считается прямолинейной. мин; во-вторых, УД считается прямолинейной.
Первое допущение приводит к существенному завышению расчетных нагрузок. Проиллюстрируем это на примере периодических графиков нагрузки трапециевидной формы с начальной  и конечной и конечной  ординатами, длительности циклов которых целое число раз размещаются в ординатами, длительности циклов которых целое число раз размещаются в  . В рамках [1] при любых . В рамках [1] при любых 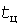 эти графики равноценны, так как имеют одинаковую прямолинейную УД (штрихи на рис. 2, а). Однако максимумы эти графики равноценны, так как имеют одинаковую прямолинейную УД (штрихи на рис. 2, а). Однако максимумы 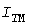 тепловой нагрузки (светлые кружки на рис. 2, б) тем меньше, чем меньше тепловой нагрузки (светлые кружки на рис. 2, б) тем меньше, чем меньше 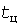 или больше или больше  . Максимум . Максимум 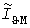 (темные кружки), определенный по УД, близок к наибольшей ординате (темные кружки), определенный по УД, близок к наибольшей ординате 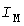 . .
Завышение 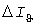 расчетной нагрузки по методу УД тем больше, чем больше отношения расчетной нагрузки по методу УД тем больше, чем больше отношения 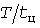 и и 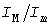 . Рис. 2 построен для . Рис. 2 построен для  и и 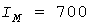 А, А,  и и  мин. Для этих значений мин. Для этих значений 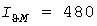 и и 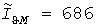 А, завышение нагрузки равно 206А или 42,9%. Тридцатиминутные же максимумы составили А, завышение нагрузки равно 206А или 42,9%. Тридцатиминутные же максимумы составили 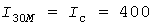 А и А и  А, что на 16,7% меньше и на 41,5% больше фактической расчетной нагрузки 480А. А, что на 16,7% меньше и на 41,5% больше фактической расчетной нагрузки 480А.
Перейдем к допущению о прямолинейности УД. Фактическая УД (рис. 3 сплошные линии) проходит выше (ниже) прямой (штрихи) в области максимальных (минимальных) значений нагрузок, поэтому это допущение занижает расчетные нагрузки.
В методе УД при определении эффективного числа 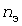 электроприемников принято допущение об одинаковости коэффициентов электроприемников принято допущение об одинаковости коэффициентов 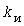 использования и использования и  формы у всех электроприемников. Погрешность формулы формы у всех электроприемников. Погрешность формулы
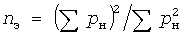
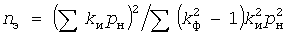
зависит от диапазона значений коэффициентов.
Деление приемников на группы А и Б, не связанное с методом УД, приводит к занижению нагрузки, так как для группы Б расчетная нагрузка принимается равной среднему значению, хотя должна быть не менее эффективного значения.
Таким образом, метод УД дает неконтролируемую погрешность в определении расчетной электрической нагрузки по нагреву.
Инерционный метод. Одним из инженерных методов расчета электрических нагрузок является «инерционный» метод [6, 7], использующий инерционное преобразование нагрузки (рис. 1, в). В этом методе учитывается известное свойство нормализации выходного процесса инерционным звеном, что позволяет считать инерционный процесс 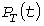 нормальным со средним значением нормальным со средним значением 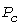 и стандартом и стандартом 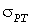 . .
Исходными для расчетов являются средние значения  и инерционные стандарты и инерционные стандарты 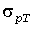 индивидуальных нагрузок или индивидуальных нагрузок или 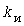 , ,  и коэффициенты и коэффициенты
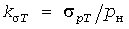 (11) (11)
инерционных отклонений.
Инерционные дисперсии нагрузок независимо работающих электроприемников суммируются, поэтому
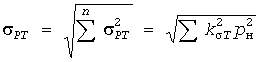 . (12) . (12)
Инерционный максимум вычисляется по формуле
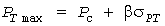 , (13) , (13)
в которой статистический коэффициент  выражается через вероятность выражается через вероятность 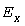 (табл. 1 в [6]). При (табл. 1 в [6]). При 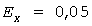  , но с небольшим запасом (не более 4,85%) нами рекомендуется значение , но с небольшим запасом (не более 4,85%) нами рекомендуется значение 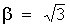 , которому соответствует , которому соответствует 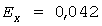 . .
Подстановка в (13) выражений (5) и (12) дает расчетную формулу метода
 , (14) , (14)
в которой в отличие от определения эффективного числа электроприемников в [3] нет упрощающего допущения о равенстве коэффициентов формы индивидуальных графиков.
Исходные для расчетов коэффициенты 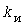 и и 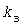 =0,8 остаются теми же , что и в методе УД. Дополнительно к ним для каждого электроприемника задаются коэффициенты =0,8 остаются теми же , что и в методе УД. Дополнительно к ним для каждого электроприемника задаются коэффициенты 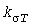 для разных для разных 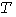 - с тем, чтобы иметь возможность рассматривать различные - с тем, чтобы иметь возможность рассматривать различные 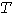 -максимумы. -максимумы.
Коэффициенты инерционных отклонений находятся экспериментально для аналогичных электроприемников. До завершения экспериментальных исследований их определяют по данным технологических расчетов о длительностях циклов работы электроприемников. В этом случае они вычисляются при 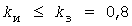 по формуле по формуле
 , (15) , (15)
которая относится к промежуточному между предельными случаю экспоненциально-косинусоидальной КФ с параметрами
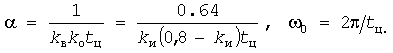 (16) (16)
Если длительности циклов не заданы, то принимается предельное для повторно-кратковременного режима значение 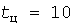 мин. мин.
Погрешность метода определяется двумя допущениями: заменой квадрата нагрузки в (1) нагрузкой и принятием  . Первое из них занижает расчетную нагрузку, а второе может дать любой знак погрешности - в зависимости от того, в какую сторону фактическое распределение инерционных нагрузок отличается от нормального. . Первое из них занижает расчетную нагрузку, а второе может дать любой знак погрешности - в зависимости от того, в какую сторону фактическое распределение инерционных нагрузок отличается от нормального.
Как отмечалось, инерционный максимум (14) может приниматься в качестве расчетной нагрузки при  . В общем же случае от этого максимума необходимо перейти к максимуму тепловой нагрузки. Соответствующая поправка . В общем же случае от этого максимума необходимо перейти к максимуму тепловой нагрузки. Соответствующая поправка  должна удовлетворять предельным соотношениям. При должна удовлетворять предельным соотношениям. При  инерционный и тепловой максимумы совпадают с наибольшим значением инерционный и тепловой максимумы совпадают с наибольшим значением
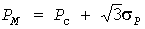
нагрузки, а потому поправка равна нулю. При 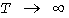 инерционный максимум стремится к средней нагрузке, а тепловой - к эффективной инерционный максимум стремится к средней нагрузке, а тепловой - к эффективной 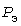 , в связи с чем поправка достигает наибольшего значения: , в связи с чем поправка достигает наибольшего значения:  . .
Вместо принятого в [6] метода сдвига здесь рекомендуется следующая формула для поправки:
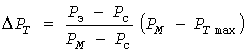 , (17) , (17)
что дает расчетную нагрузку
 . (18) . (18)
Расчетные формулы (14) и (18) довольно просты, поэтому могут использоваться даже для вычислений на микрокалькуляторе.
Эквивалентный параметр КФ. При небольших различиях в номинальных мощностях и интенсивностях  в предельном соотношении (10) параметр КФ в предельном соотношении (10) параметр КФ
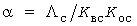
выражается через средние значения индивидуальных характеристик:
 . .
В общем случае его приходится выбирать из условия воспроизведения той или иной характеристики суммарной нагрузки. В рассматриваемой задаче естественно потребовать, чтобы инерционный стандарт (12) совпал со стандартом
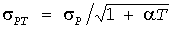 , (19) , (19)
вычисленным по экспоненциальной КФ. Отсюда получим эквивалентный параметр
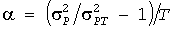 . (20) . (20)
Квадратичный метод. В основу разработанного инженерного «квадратичного» метода (название - условное) положена формула вида (13), но в применении к графику  квадрата тепловой нагрузки: квадрата тепловой нагрузки:
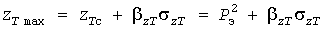 . (21) . (21)
Принципиальная трудность состоит в том, что вероятностное распределение процесса  не известно, поэтому при заданной граничной вероятности не известно, поэтому при заданной граничной вероятности 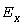 статистический коэффициент статистический коэффициент 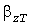 не определен. Нормализация же процесса не определен. Нормализация же процесса 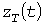 происходит при очень больших постоянных нагрева, в связи с чем не всегда можно принимать значение происходит при очень больших постоянных нагрева, в связи с чем не всегда можно принимать значение 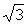 , когда , когда
 . (22) . (22)
До завершения исследований в качестве приближенного решения для любых постоянных времени примем величину (9), относящуюся к 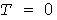 . .
Стандарт процесса  может быть вычислен в предположении о нормальном распределении нагрузок, когда КФ квадратов нагрузки и КФ нагрузки связаны соотношением может быть вычислен в предположении о нормальном распределении нагрузок, когда КФ квадратов нагрузки и КФ нагрузки связаны соотношением
 . .
С учетом формул (10) и (19) получим
 , (23) , (23)
где параметр 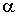 вычисляется согласно (20). вычисляется согласно (20).
Таким образом, расчетная нагрузка в квадратичном методе определяется выражением
 . (24) . (24)
Вычисления значений  и и 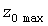 вручную довольно трудоемкие, поэтому их следует выполнять на ЭВМ. вручную довольно трудоемкие, поэтому их следует выполнять на ЭВМ.
Метод имитации. Из-за нелинейности правой части аналитическое решение уравнения (1) при случайной нагрузке сопряжено с непреодолимыми трудностями. Формально для нормально распределенных нагрузок с КФ вида (10) плотность распределения записывается в виде ряда (формула (34.13) в [9]). Доступная в проектировании информация дает возможность вычислить два члена ряда, что совершенно недостаточно, так как и при четырех членах ряд дает противоречащий физическому смыслу результат: отрицательные значения на рис. 26 в [9] сугубо положительной плотности распределения температур.
В связи с этим применяют методы имитационного моделирования суммарной нагрузки на ЭВМ (методы Монте-Карло). При известных индивидуальных графиках нагрузки  реализации процесса реализации процесса  получают разыгрыванием случайных сдвигов между получают разыгрыванием случайных сдвигов между  [6, 7]. Для массовых электроприемников более эффективным является использование предельного соотношения (10). [6, 7]. Для массовых электроприемников более эффективным является использование предельного соотношения (10).
Существуют методы, которые позволяют сразу получать реализации случайного процесса с заданной КФ (например, [8]). Однако в соответствии с физикой рассматриваемой задачи целесообразно имитировать 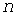 индивидуальных случайных процессов индивидуальных случайных процессов 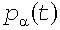 , затем их суммировать. В отличие от метода «элементных процессов» [6] процессы , затем их суммировать. В отличие от метода «элементных процессов» [6] процессы 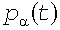 имеют фактические значения имеют фактические значения  , ,  и и  , а следовательно и стандарты , а следовательно и стандарты  . Для того, чтобы суммарный процесс имел вид (10), КФ этих процессов должна быть экспоненциальной: . Для того, чтобы суммарный процесс имел вид (10), КФ этих процессов должна быть экспоненциальной:
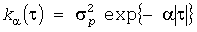
с параметром (20).
Случайные процессы с затухающими КФ могут имитироваться в виде одной реализации очень большой длительности или ансамбля большого количества 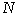 реализаций. Далее принята имитация «по ансамблю», преимуществом которой является небольшая длительность каждой реализации: для окончания переходного случайного процесса реализаций. Далее принята имитация «по ансамблю», преимуществом которой является небольшая длительность каждой реализации: для окончания переходного случайного процесса  она должна составлять (3 - 5) она должна составлять (3 - 5) . .
Имитация процессов  сводится к генерированию экспоненциальных распределений длительностей импульсов и пауз с параметрами сводится к генерированию экспоненциальных распределений длительностей импульсов и пауз с параметрами
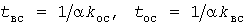 . (25) . (25)
После суммирования 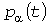 полученная реализация (рис. 4, а) возводится в квадрат, решается уравнение (1) с правой частью полученная реализация (рис. 4, а) возводится в квадрат, решается уравнение (1) с правой частью 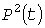 , а затем из полученного процесса извлекается квадратный корень (рис.4, б). , а затем из полученного процесса извлекается квадратный корень (рис.4, б).
На рис. 4 показано 10 из 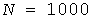 реализаций, полученных описанным способом. Для момента времени реализаций, полученных описанным способом. Для момента времени 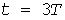 совокупность ординат (кружки на рис. 4, б) позволяет построить УД тепловых нагрузок и с заданной граничной вероятностью совокупность ординат (кружки на рис. 4, б) позволяет построить УД тепловых нагрузок и с заданной граничной вероятностью 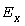 определить расчетную нагрузку: для Примера при определить расчетную нагрузку: для Примера при  она составила 48,7 кВт. она составила 48,7 кВт.
Имитационный метод в рамках общепринятых допущений и доступной в проектировании исходной информации можно считать точным. Наличие реализаций суммарной нагрузки (рис. 3) позволяет решать и другие задачи электроснабжения, в первую очередь, нелинейные (оценка теплового износа, эффективности регулирования и др.).
Перерасчет максимумов. Принятое в методе УД значение 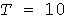 мин имеют проводники небольшого сечения: например, изолированные провода в трубе до 16 мм2, а у кабелей вообще мин имеют проводники небольшого сечения: например, изолированные провода в трубе до 16 мм2, а у кабелей вообще 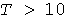 мин [3]. В связи с этим для исключения завышения нагрузок необходимо выполнять перерасчет десятиминутной тепловой нагрузки на фактическое значение постоянной времени нагрева. Согласно (13) и (21) формулы перерасчета имеют вид: мин [3]. В связи с этим для исключения завышения нагрузок необходимо выполнять перерасчет десятиминутной тепловой нагрузки на фактическое значение постоянной времени нагрева. Согласно (13) и (21) формулы перерасчета имеют вид:
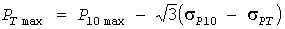 , (26) , (26)
 (27) (27)
Как показано в [7], обычно используется формула пересчета, в которой поправка обратно пропорциональна  , относится к нереализуемому на практике предельному случаю отсутствия корреляционных связей между соседними ординатами. , относится к нереализуемому на практике предельному случаю отсутствия корреляционных связей между соседними ординатами.
Поскольку заранее не известно, какое сечение будет выбрано, целесообразно сразу рассчитывать зависимость расчетной нагрузки от постоянной нагрева 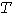 в пределах ее изменения от 0 до значения, когда расчетная нагрузка становится равной в пределах ее изменения от 0 до значения, когда расчетная нагрузка становится равной 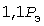 . Это не встречает затруднений, так как в исходных данных дается зависимость коэффициентов инерционных отклонений от постоянной нагрева. . Это не встречает затруднений, так как в исходных данных дается зависимость коэффициентов инерционных отклонений от постоянной нагрева.
Сопоставление методов расчета. Корректность инженерных методов проверяется экспериментально или методом имитации. Такая проверка была выполнена для случаев, когда относительная погрешность  предлагаемых инженерных методов ожидалась наибольшей: в 180 примерах количество электроприемников изменялось от 4 до 15, коэффициенты использования от 0,1 до 0,6, длительности циклов от 2 до 10 мин, постоянные времени от 10 до 20 мин при соотношении номинальных мощностей в группе 1 к 10. предлагаемых инженерных методов ожидалась наибольшей: в 180 примерах количество электроприемников изменялось от 4 до 15, коэффициенты использования от 0,1 до 0,6, длительности циклов от 2 до 10 мин, постоянные времени от 10 до 20 мин при соотношении номинальных мощностей в группе 1 к 10.
На рис. 5 приведены пределы полученных погрешностей. Наилучший результат дает квадратичный метод, погрешности расчетов по которому не вышли за десятипроцентные границы (пунктир). Диапазоны погрешностей применения формул (18)и (22) практически одинаковы: 25,2 и 25,1%, но инерционный метод завышает нагрузку до 15,2%, а формула (18) - занижает до 17,2%.
С увеличением количества электроприемников (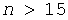 ) даже при ) даже при 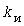 =0,1 погрешности заметно уменьшаются. =0,1 погрешности заметно уменьшаются.
Во всех случаях погрешность предлагаемых инженерных методов намного меньше, чем у метода УД, который завышает расчетную нагрузку до 87,3%.
Для Примера формула (14) дала погрешность всего -0,86%, несмотря на то, что средняя нагрузка была меньше, чем 0,9 . Это объясняется тем, что занижение нагрузки из-за использования процесса . Это объясняется тем, что занижение нагрузки из-за использования процесса 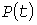 , а не его квадратов скомпенсировалось завышенным значением , а не его квадратов скомпенсировалось завышенным значением 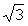 статистического коэффициента. Формула (18) привела к погрешности 5,14%. Случайно оказалось, что значение статистического коэффициента. Формула (18) привела к погрешности 5,14%. Случайно оказалось, что значение 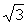 практически совпало с практически совпало с 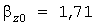 , поэтому формулы (22) и (24) дали близкие результаты с погрешностями всего -1,69 и -1,88%. По методу же УД расчетная нагрузка оказалась завышенной на 48,6%. , поэтому формулы (22) и (24) дали близкие результаты с погрешностями всего -1,69 и -1,88%. По методу же УД расчетная нагрузка оказалась завышенной на 48,6%.
Выводы.
1. Принятое в действующих Указаниях понятие расчетной нагрузки по нагреву в виде «инерционного» максимума десятиминутной тепловой нагрузки отражает физику задачи. Понятие же «кумулятивного» максимума получасовой средней нагрузки из ПУЭ приводит к противоречащим смыслу результатам.
Метод УД сыграл положительную роль в развитии теории электрических нагрузок, но в настоящее время требует замены из-за существенного завышения расчетных нагрузок.
Определение расчетных электрических нагрузок по нагреву целесообразно выполнять точным методом имитации, допуская применение инженерных методов: инерционного и квадратичного.
ПЕРЕЧЕНЬ ССЫЛОК
Указания по определению электрических нагрузок в промышленных установках// Инструктивные материалы по проектированию электротехнических промышленных установок.-М.: Энергия, 1968, №6.-с.3-17.
Каялов Г.М. Основы анализа нагрузок и расчета электрических сетей промышленных предприятий.-Электричество, 1951, №4.-с. 28-37.
Электрические нагрузки промышленных предприятий// С.Д. Волобринский, Г.М. Каялов и др.-М.-Л.: Энергия, 1964.-304 с.
Правила устройства электроустановок.-М.: Энергоатомиздат, 1985.-640 с.
ГОСТ 13109-87. Электрическая энергия. Требования к качеству электрической энергии в электрических сетях общего назначения.- Введ. 01.01.89.
Шидловский А.К., Куренный Э.Г. Введение в статистическую динамику систем электроснабжения. - К.: Наукова думка, 1984. - 271 с.
Шидловский А.К., Вагин Г.Я., Куренный Э.Г. Расчеты электрических нагрузок систем электроснабжения промышленных предприятий. - М.: Энергоатомиздат, 1992.-224 с.
8. Куренный Э.Г., Погребняк Н.Н. «Эстафетный» метод имитации случайных электроэнергетических процессов. - Техническая электродинамика, 1990, №3.- с.3-6.
9. Свешников А.А. Прикладные методы теории случайных функций. - М.: Наука, 1968.- 463 с.
|
|
