| |
УДК 621.3.05 :519.2
АНАЛИЗ РЕЖИМОВ СЕТЕЙ ЭЛЕКТРОСНАБЖЕНИЯ ПРОМЫШЛЕННЫХ
ПРЕДПРИЯТИЙ ИМИТАЦИОННЫМИ МЕТОДАМИ
Э.Г. Куренный,доктор техн. наук, Н.Н. Погребняк, аспирантка ДГТУ- Минвуз Украины
Процессы в сетях электроснабжения обусловлены суммированием электрических нагрузок от группы n электроприемников, а потому являются случайными. Помимо традиционных экспериментальных и аналитических методов их анализа все чаще используются методы имитации( Монте-Карло, статистического моделирования [1]), которые позволяют получать реализации случайных процессов с заданными характеристиками. В статье показывается их эффективность на примере определения расчетной электрической нагрузки по нагреву, но все выводы справедливы и для задач оценки качества напряжения, регулирования и прогнозирования процессов.
Общие соображения. Методы имитации применяют когда эксперимент затруднен или невозможен(для сетей проектируемых предприятий), а аналитическое решение либо отсутствует (при нелинейных задачах), либо требует громоздких выкладок.
При имитации основной является проблема проверки качества получаемых реализаций. Поскольку имитация основана на генерации псевдослучайных чисел, то всегда могут появиться реализации , которые не обеспечивают точное воспроизведение заданных характеристик. Поэтому во всех случаях требуется проверка с помощью известных критериев математической статистики. Такой проверки достаточно, если известно, что исходная информация обеспечивает решение задачи. В этом случае имитация полностью заменяет «чистый» эксперимент. Если доказательства достаточности исходных характеристик отсутствуют, то требуется, по возможности, использовать тестовые задачи.
Необходимость и эффективность вероятностных методов обусловлена тем, вместо всего диапазона (Pм, PМ) возможных значений исследуемой случайной величины P в расчетах используется меньший диапазон (Pmin, Pmax), выход за пределы которого возможен с малой вероятностью ER. Это дает возможность экономить средства на сеть электроснабжения.
В общем случае для определения расчетных значений необходимо знать закон вероятностного распределения величины P, например, функцию распределения F(P), разновидностью которой является упорядоченная диаграмма (уд). Считая, что выход за пределы расчетного диапазона в меньшую и большую сторону допустим с равной граничной вероятностью Ex=ER/2, получим уравнение для определения расчетных значений:
F(Pmin)=Ex, F(Pmax)=1-Ex. (1)
Обычно расчетные значения представляют в виде
Pmin=Pc-bsP , Pmax=Pc+bsP , (2)
где Pc и sP - среднее значение и стандарт, b - статистический коэффициент. Если закон распределения известен, то b выражается через граничную вероятность. В методе УД [2] принято значение b=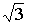 , которому при нормальном распределении соответствует Ex=0.042. В ГОСТ 13109-87 для показателей качества напряжения нормируется значение Ex=0.05. , которому при нормальном распределении соответствует Ex=0.042. В ГОСТ 13109-87 для показателей качества напряжения нормируется значение Ex=0.05.
Необходимость имитации. В [2] допустимость нагрева проводников оценивается по максимальной температуре 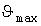 его перегрева. В относительных единицах (о.е.) упрощенное уравнение нагрева проводника с постоянной времени нагрева Т имеет вид его перегрева. В относительных единицах (о.е.) упрощенное уравнение нагрева проводника с постоянной времени нагрева Т имеет вид
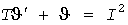 , (3) , (3)
где 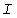 -ток, -ток, 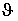 -температура перегрева. Средняя температура -температура перегрева. Средняя температура  в о.е. равна квадрату эффективной нагрузки Iэ. в о.е. равна квадрату эффективной нагрузки Iэ.
В силу нелинейности правой части задача о нахождении функции распределения 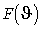 аналитического решения фактически не имеет. Представление же ее в виде ряда [3] даже для частного случая нормального распределения нагрузки требует недоступного для практики объема информации, а использование четырех членов ряда приводит к противоречащим физике результатам: отрицательные значения плотности распределения на рис. 26 и 27 в [3]. В связи с этим для решения задачи необходимо использовать методы имитации, которые позволяют оценить корректность инженерных методов расчета нагрузок. аналитического решения фактически не имеет. Представление же ее в виде ряда [3] даже для частного случая нормального распределения нагрузки требует недоступного для практики объема информации, а использование четырех членов ряда приводит к противоречащим физике результатам: отрицательные значения плотности распределения на рис. 26 и 27 в [3]. В связи с этим для решения задачи необходимо использовать методы имитации, которые позволяют оценить корректность инженерных методов расчета нагрузок.
Для проверки взят частный случай нагрева проводника нагрузкой в виде последовательности прямоугольных импульсов величиной I и пауз с экспоненциальными распределениями их длительностей. Если tц- длительность цикла, то при коэффициенте включения 0.5 плотность распределения температур дается формулой
 , (4) , (4)
где 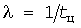 - частота, - частота,  - гамма-функция. - гамма-функция.
Имитация ансамбля реализаций. В действующих сетях связь между ординатами нагрузки ослабевает с увеличением промежутка времени между ними. Это позволяет исследовать нагрузку по одной реализации, достаточно продолжительной для реализации вероятностных характеристик. Обычно и методы имитации разрабатывались под обработку «по реализации».
На наш взгляд, несмотря на наглядность такого подхода, целесообразнее использовать имитацию ансамбля реализаций. Во-первых, в этом случае возможно изучение переходного случайного процесса нагрева и, во-вторых, существенно уменьшить длительность каждой реализации, особенно при исследовании теплового износа.
Требуемое количество N реализаций в ансамбле устанавливается известными формулами математической статистики. Имитация сводится к получению реализаций нагрузки и преобразованию их в соответствии с математической моделью объекта: для рассматриваемой задачи - уравнением (3).
При повторно-кратковременном режиме нагрузка каждого электроприемника имитируется в соответствии с вероятностными распределениями длительностей tв импульсов tо пауз. Для этого используются соответствующие преобразования значений, получаемых от двух стандартных генераторов равномероно распределенных случайных чисел 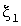 и и 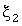 . Например, при экспоненциальных распределениях со средними длительностями . Например, при экспоненциальных распределениях со средними длительностями  и и 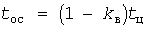 преобразования имеют вид: преобразования имеют вид: 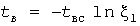 , ,  . .
Качество работы генераторов проверяется по отсутствию связи между случайными значениями. Если качество неудовлетворительное, то случайная последовательность либо генерируется заново, либо корректируется (например, согласно [4]).
Реализации суммарной нагрузки получаются суммированием индивидуальных реализаций, что соответствует физике задачи.
Преобразование реализаций согласно [3] не требует численного решения уравнения, так как сводится к применению интеграла Дюамеля. Вначале наблюдается переходный процесс, а спустя (3-5)T практически наступает стационарное состояние. В связи с этим необходимые длительности реализаций групповых нагрузок не превышают 5T при оценке как максимальной температуры, так и теплового износа.
Имитационное моделирование индивидуальных нагрузок с экспоненциальными распределениями длительностей импульсов и пауз при разных  показало очень хорошее совпадение с теоретическим распределением по критериям согласия Пирсона и Колмогорова. Это иллюстрирует рис. 1, где показаны теоретические функции распределения для четырех значений показало очень хорошее совпадение с теоретическим распределением по критериям согласия Пирсона и Колмогорова. Это иллюстрирует рис. 1, где показаны теоретические функции распределения для четырех значений 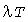 . Полученные имитацией ординаты статистических функций распределения (светлые кружки) почти полностью совпадают с теоретическими. Приняв . Полученные имитацией ординаты статистических функций распределения (светлые кружки) почти полностью совпадают с теоретическими. Приняв  и проведя горизонталь и проведя горизонталь 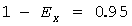 , получим расчетные максимумы температуры (темные кружки). Чем больше , получим расчетные максимумы температуры (темные кружки). Чем больше 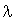 , тем меньше длительность цикла, тем меньше максимальный перегрев проводника. , тем меньше длительность цикла, тем меньше максимальный перегрев проводника.
Проверка инженерных методов. При разработке метода УД для предельного уменьшения объема исходной информации об индивидуальных графиках p(t) активной мощности в (3) вместо графика нагрузки была использована его УД. Это привело к завышению расчетной нагрузки - тем большему, чем меньше средняя длительность циклов(рис. 2.9 в [5]). В связи с этим возникает необходимость в замене этого метода.
Поскольку точного аналитического решения задачи нет, возможны различные инженерные методы расчета. На наш взгляд, в их основу следует положить метод, который во многих случаях дает близкий к точному результат.
Этому естественному требованию удовлетворяет «инерционный» метод [1, 5], в котором используют инерционные нагрузки IT(t), получаемые решением уравнения
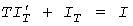 .(5) .(5)
Левые части уравнений (3) и (5) совпадают, поэтому качественно процессы  и IT(t) одинаково отражают основной фактор решаемой задачи - тепловую инерцию проводника. Более того, при небольших различиях в среднем Iс и эффективном значениях нагрузки результаты оказываются близкими: в о.е. и IT(t) одинаково отражают основной фактор решаемой задачи - тепловую инерцию проводника. Более того, при небольших различиях в среднем Iс и эффективном значениях нагрузки результаты оказываются близкими: в о.е. 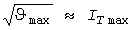 . При допустимой относительной погрешности . При допустимой относительной погрешности  согласно (V.15) из [1] это выполняется при согласно (V.15) из [1] это выполняется при
 . (6) . (6)
Такие случаи часто встречаются в практике, о чем свидетельствует использование в ПУЭ получасовых средних, а не эффективных нагрузок.1
При больших различиях необходимо внесение поправок в результаты расчетов по инерционному методу. Вместо «метода сдвига» (рис.74 в [1]) здесь предлагается использовать поправку
 , (7) , (7)
где  - расчетная ордината графика нагрузки. - расчетная ордината графика нагрузки.
Корректность инженерных методов поверялась путем имитации ансамблей реализаций 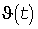 для большого количества примеров. Варьировались номинальные мощности, средние длительности циклов, количество электроприемников, а также вероятностные распределения длительностей циклов. Было показано, что погрешность существующих Указаний [2] достигает десятков процентов, в то время как имитационный метод с поправкой (7) дает единицы процентов. Вместе с тем, при значительном расхождении между номинальными мощностями встречались случаи, когда погрешность превышала 10%. В связи с этим было предложено более сложное выражение для поправок, чем (6), которое для краткости здесь не приводится. для большого количества примеров. Варьировались номинальные мощности, средние длительности циклов, количество электроприемников, а также вероятностные распределения длительностей циклов. Было показано, что погрешность существующих Указаний [2] достигает десятков процентов, в то время как имитационный метод с поправкой (7) дает единицы процентов. Вместе с тем, при значительном расхождении между номинальными мощностями встречались случаи, когда погрешность превышала 10%. В связи с этим было предложено более сложное выражение для поправок, чем (6), которое для краткости здесь не приводится.
Тестовая задача для суммарных нагрузок. Качественная близость уравнений (3) и (5) позволяет использовать в качестве тестовой задачу нахождения функции распределения 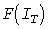 инерционных нагрузок при нормальном распределении нагрузки. В силу линейности уравнения (5) распределение инерционных нагрузок также будет нормальным. инерционных нагрузок при нормальном распределении нагрузки. В силу линейности уравнения (5) распределение инерционных нагрузок также будет нормальным.
В этом случае формула (2) будет теоретически точной, так как статистический коэффициент известен (табл.1 [1]). Инерционный стандарт  вычисляется через корреляционную функцию вычисляется через корреляционную функцию 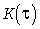 нагрузки, поэтому при имитации достаточно проверить точность ее воспроизведения. нагрузки, поэтому при имитации достаточно проверить точность ее воспроизведения.
Для надежности, помимо проверки нормальности распределений полученных инерционных нагрузок с параметрами  и и  , целесообразно проверить корреляционную функцию квадратичного процесса , целесообразно проверить корреляционную функцию квадратичного процесса 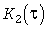 . Для нормальных распределений она должна быть близкой к теоретическому значению . Для нормальных распределений она должна быть близкой к теоретическому значению
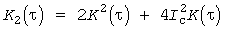 . .
Однако при этом требуемая длительность реализаций возрастет на величину учитываемого аргумента  . .
Выводы. 1. Методы имитации целесообразно применять для решения нелинейных задач и проверки корректности инженерных методов расчета показателей режимов сетей электроснабжения.
Имитацию случайных процессов следует осуществлять в виде ансамбля реализаций небольшой длительности, а не одной реализации большой продолжительности.
Из-за существенного завышения расчетных электрических нагрузок метод упорядоченных диаграмм необходимо заменить инерционным методом или использовать методы имитации.
СПИСОК ЛИТЕРАТУРЫ
1. Шидловский А.К., Куренный Э.Г. Введение в статистическую динамику систем электроснабжения. - К.: Наукова думка, 1984. - 271 с.
2. Указания по определению электрических нагрузок в промышленных установках// Инструктивные материалы по проектированию электротехнических промышленных установок. М.: Энергия, 1968, №6.- с.3-17.
Свешников А.А. Прикладные методы теории случайных функций. - М.: Наука, 1968.- 463 с.
4. Куренный Э.Г., Погребняк Н.Н. «эстафетный» метод имитации случайных электроэнергетических процессов. - Техническая электродинамика, 1990, №3.- с. 3-6.
5. Расчеты электрических нагрузок систем электроснабжения промышленных предприятий/ А.К. Шидловский, Г.Я. Вагин, Э.Г. Куренный. - М.: Энергоатомиздат, 1992.-224 с.
|
|


























