

О.І. Толочко, П.Х. Коцегуб, П.І. Розкаряка, З.І. Кателло, ДонНТУ
Численное Решение алгебраического УРАВНЕНИя В РЕАЛЬНОМ ВРЕМЕНИ ПРИ РЕАЛИЗАЦИИ ОПТИМАЛЬНОГО алгоритма УПРАВЛЕНИЯ
ПОЗИЦИОННЫМ ЭЛЕКТРОПРИВОДОМ
Запропоновані методика i Simulink-моделі розв‘язання алгебраїчного рівняння, що входить до алгоритму формування оптимальних діаграм переміщення, в реальному часі без використання апарату S-функцій.
Предложены методика и Simulink-модели решения алгебраического уравнения, входящего в алгоритм формирования оптимальных диаграмм перемещения, в реальном времени без использования аппарата S-функций.
Method and Simulink-models of algebraic equation solution which appear to algorithm of formatting optimal position diagram on the real time has been proposed. It needn’t creating S-function.
Введение. Для систем позиционного электропривода предложено множество диаграмм изменения положения, скорости, ускорения и рывка в функции времени при перемещении механизма из одного заданного положения в другое. Основными из них являются диаграммы, оптимальные по быстродействию и по тепловым потерям в якоре двигателя постоянного тока или в роторе асинхронного двигателя, с учетом ограничений на скорость, ускорение, ток двигателя и рывок.
Увеличение цен на энергоносители повышает актуальность принятия решений, направленных на снижения непроизводительных затрат электроэнергии. С этой точки зрения для управления позиционными электроприводами целесообразно использовать задающие устройства (ЗУ), формирующие диаграммы перемещения, оптимальные или квазиоптимальные по тепловым потерям. Такие ЗУ имеют достаточно сложный алгоритм формирования управляющих воздействий и могут быть успешно реализованы только в цифровой форме.
Для программной реализации алгоритмов управления электромеханическими системами в реальном времени обычно используют один из универсальных или специализированных языков программирования. Более простым и удобным способом решения поставленной задачи является использование программы структурного математического моделирования Simulink пакета MatLab в режиме реального времени, который обеспечивается приложением Real Time WorkShop [1]. Достоинствами такого способа реализации является наглядность алгоритма, который представляется в виде структурной модели, удобство его отладки и корректировки, отсутствие необходимости применения языков программирования, использование одной и той же среды для математического моделирования и для управления приводом.
Однако при разработке Simulink-моделей ЗУ, способных функционировать в реальном времени, нужно учесть, что далеко не все блоки стандартных библиотек можно использовать совместно с приложением Real Time WorkShop. Кроме того, алгоритм формирования оптимальных диаграмм перемещения с учетом действия на привод постоянного момента статического сопротивления, содержит процедуру численного решения алгебраического уравнения 4-ой степени, что может увеличить время формирования управляющего воздействия до недопустимой величины.
Целью работы является разработка Simulink-модели, осуществляющей решение алгебраического уравнения, входящего в алгоритм формирования оптимальных диаграмм перемещения, в реальном времени, и оценка машинного времени, затрачиваемого на реализацию этого алгоритма в выбранной программной среде.
Материал и результаты исследования
На рис. 1 приведены оптимальные по тепловым потерям двигателя диаграммы отработки заданного перемещения αз за заданное время τ0 при наличии ограничений на ток i0 и скорость ν0 с учетом постоянно действующего статического момента, представленного на рисунке пропорциональной ему статической составляющей тока двигателя is. Сочетание перечисленных параметров является таковым, что диаграмма имеет участки работы двигателя в режиме токоограничения (τ1) и в режиме ограничения скорости (τy).
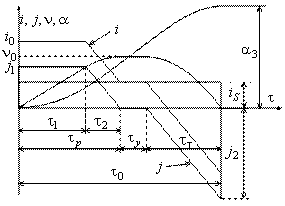
Рис. 1. Оптимальная диаграмма отработки заданного перемещения под нагрузкой
В работах [2, 3] для определения параметров этой диаграммы приведены формулы, представление которых в виде блоков Simulink не вызывает особых трудностей. Но для вычисления максимального значения динамического тока j2 при торможении привода аналитическое выражение отсутствует. В [2] показано, что искомую величину можно найти решением неполного алгебраического уравнения 4-ой степени с действительными коэффициентами
![]() . (1)
. (1)
Из физического смысла решаемой задачи следует, что искать при этом следует действительный корень уравнения (1), принадлежащий интервалу [0, i0+ is].
Одними из самых простых численных методов решения алгебраических и трансцендентных уравнений являются итерационные методы половинного деления, хорд и касательных [4].
Анализ полиномиальной функции f(j2) в правой части уравнения (1) показывает, что в области реальных параметров такой корень всегда существует и является единственным. Кроме того, график этой функции имеет на конце интервала [0, i0+ is] большую крутизну и удовлетворяет условию f(j2)· f”(j2)>0, что делает рациональным решение уравнения (1) методом касательных с начальным приближением корня, равным i0+ ic.
В библиотеке Math приложения Simulink имеется блок Algebraic Constraint, обеспечивающий нахождение корней уравнения вида f(x)=0 путем создания алгебраической петли, но такой способ решения уравнений неприемлем для приложения Real Time WorkShop.
На рис. 2 представлена блок-схема алгоритма уточнения заданного начального приближения x0 корня уравнения f(x)=0 методом касательных (называемым также методом Ньютона), а на рис. 3 – Simulink-модель этого итерационного алгоритма, в которой для организации циклического процесса использована подсистема с разрешающим входом (Enabled Subsystem).
Работа подсистемы Enabled Subsystem (j2_kasat) осуществляется только тогда, когда справедливо неравенство |h|>ε, где ε – заданная в блоке Const переменной e точность решения уравнения.
В блоке Memory, осуществляющем запаздывание на один шаг численного интегрирования, параметр Initial Condition (начальное условие) установлен равным единице, чтобы обеспечить запуск итерационного процесса без задержки на первом шаге. Развернутая модель этой подсистемы приведена на рис. 4.
В подсистеме j2_kasat формируется начальное приближение корня x0=i0+ic и выполняется тело итерационного цикла.
Значения функции, составляющей левую часть уравнения (1)
![]()
и ее производной
![]()
вычисляются в подсистемах f(x) и df(x).
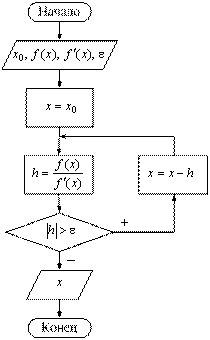
Рис. 2. Блок-схема уточнения корня
уравнения
методом касательных
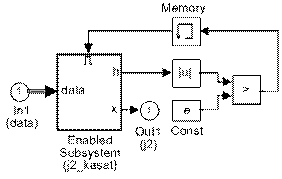
Рис. 3. Simulink-модель решения уравнения (1) в
реальном времени
Если разность
между двумя последовательными приближениями ![]() не обеспечивает заданной точности
не обеспечивает заданной точности ![]() , то выполняется следующая
итерация. При достижении заданной точности итерационный процесс прекращается.
Параметр Threshold блока Switch установлен равным 0.5. На входной
порт In1 (data)
поступает вектор сигналов, необходимых для расчета коэффициентов полиномиальных
функций f(x) и f’(x).
, то выполняется следующая
итерация. При достижении заданной точности итерационный процесс прекращается.
Параметр Threshold блока Switch установлен равным 0.5. На входной
порт In1 (data)
поступает вектор сигналов, необходимых для расчета коэффициентов полиномиальных
функций f(x) и f’(x).
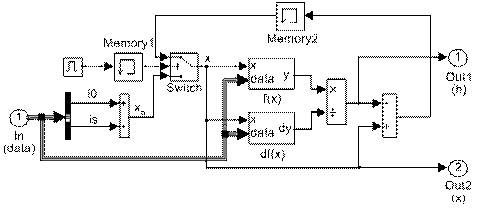
Рис. 4. Развернутая модель подсистемы Enabled Subsystem (j2_kasat) при решении уравнения (1)
методом касательных
Как известно [4], метод Ньютона при неудачно выбранном начальном приближении может оказаться расходящимся. В этом случае для нахождения корня можно воспользоваться методом хорд или методом половинного деления. Для их реализации в модели рис. 3 достаточно изменить структуру подсистемы Enabled Subsystem.
Блок-схема алгоритма уточнения корня алгебраического или трансцендентного уравнения методом хорд или методом половинного деления показана на рис. 5, а соответствующая этому алгоритму развернутая Simulink-модель подсистемы Enabled Subsystem – на рис. 6.
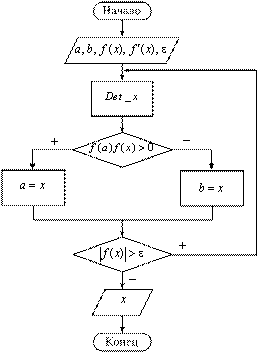
Рис. 5. Блок-схема уточнения корня уравнения
методами хорд и половинного деления
Блок Det_x алгоритма рис.5 и модели рис. 6 выполняет уточнение корня х в теле итерационного циклического процесса для метода хорд по формуле
![]() , (3)
, (3)
а для метода половинного деления – по формуле
![]() , (4)
, (4)
где a=0 и b=i0+ic – границы интервала существования корня.
Блоки знаковых функций Sign1, Sign2 и управляемые переключатели Switch1, Switch2 используются для постепенного сужения интервала существования корня за счет изменения его левой a_new или правой b_new границ.
Условие выполнения итерационного цикла имеет вид |f(x) |>ε.
Исследования системы управления показали, что для решения уравнения (1) с точностью ε=0.001 методом касательных понадобилось 3 итерации, методом хорд – 4 итерации, методом половинного деления – 7 итераций.
Предложенные модели были успешно
использованы в качестве фрагментов системы управления позиционным электроприводом
экспериментальной установки в операционной системе реального времени QNX. Значение самой малой постоянной времени электромеханической
системы – некомпенсируемой постоянной ![]() составляло 5 мс. Управляющая ЭВМ (Pentium III, 600 МГц, ОЗУ – 64 Мб) осуществляла опрос каналов
АЦП, расчет и выдачу управляющих воздействий с частотой 2 кГц.
составляло 5 мс. Управляющая ЭВМ (Pentium III, 600 МГц, ОЗУ – 64 Мб) осуществляла опрос каналов
АЦП, расчет и выдачу управляющих воздействий с частотой 2 кГц.
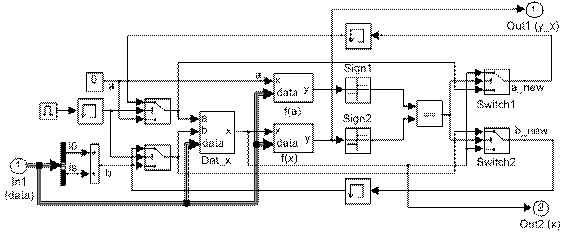
Рис. 6. Развернутая модель подсистемы Enabled Subsystem (j2_kasat) при решении уравнения (1)
методами хорд или половинного деления
Общее время, затраченное ЭВМ на расчет выходных сигналов задатчика положения в соответствии с алгоритмом, приведенным в [2], а также регуляторов тока, скорости и положения трехконтурной системы управления позиционным электроприводом, составило 120 мкс.
Таким образом, расчет приведенного алгебраического уравнения любым из методов осуществляется за время, меньшее самой малой постоянной времени электромеханической системы Tμ.
Выводы
1. Численное решение несложных трансцендентных и алгебраических уравнений может быть успешно выполнено в реальном времени в среде MatLab ® Simulink ® Real Time WorkShop.
2. Для решения алгебраического уравнения (1), входящего в алгоритм формирования оптимальных по тепловым потерям диаграмм перемещения, лучше всего использовать метод касательных, отличающийся простотой модели алгоритма уточнения корня в реальном времени и быстрой сходимостью итерационного процесса.
3. Предложенную методику и Simulink-модели решения уравнений в реальном времени, не требующие написания S-функций, можно использовать и для решения других задач в области цифрового управления электромеханическими системами.
1. Коцегуб П.Х., Толочко О.И., Федоряк Р.В. Практическая реализация цифровых САУ в среде пакета МАТЛАБ с использованием платформы реального времени «QNX TARGET» // Вісник Національного Технічного Університету "Харківський політехнічний інститут". Збірка наукових праць “Проблеми автоматизованого електроприводу. Теорія i практика”.– Харків: НТУ ”ХПI”, 2002, №12. – Т.1. – С. 98-101.
2. Костенко В.И., Коцегуб П.Х., Розкаряка П.И., Толочко О.И. Формирование оптимальных по нагреву диаграмм отработки заданных перемещений при наличии постоянного статического момента на валу двигателя // Вісник Національного Технічного Університету "Харківський політехнічний інститут". Збірка наукових праць “Проблеми автоматизованого електроприводу. Теорія i практика”.– Харків: НТУ ”ХПI”, 2002, №12. – Т.2. – С. 350-354.
3. Карнюшин Л.В., Пышкало В.Д., Рогачев А.И. Области существования оптимального управления электроприводами // Электромашиностроение и электрооборудование. Выпуск 15. Киев, «Техника», 1972. – С. 3-8.
4. Демидович Б.П., Марон И.А. Основы вычислительной математики. М., Наука, 1970 г., 664 с.
Рекомендовано до публікації д.т.н. С.В. Карасем 15.02.06
