Разработка дискретного интегратора, вЫполняющего

численное интегрирование методом симпсона

Толочко О.И., Розкаряка П.И., Кателло З.И.

Донецкий национальный технический университет

 

Чаще всего при интегрировании в реальном времени используются методы прямоугольников и трапеций. Именно такие методы численного интегрирования (ЧИ) используются в блоке Discrete-Time Integrator приложения Simulink пакета Matlab. Заметим, что вышеназванный программный продукт можно использовать не только для математического моделирования, но и для реализации цифровых алгоритмов управления в реальном времени.

При решении некоторых задач цифрового управления электромеханическими объектами возникает необходимость повышения точности численного интегрирования. Эта задача может быть решена использованием метода Симпсона. Для разработки такого интегратора воспользуемся формулой расчета площади параболической трапеции, т.е. фигуры, ограниченной параболой, проходящей через три точки с известными координатами (t_i, u_i), (t_i+1, u_i+1) та (t_i+2, u_i+2) и прямыми t=t₁, t=t_i+2 и u=0:

,                                                                                                                                  (1)

где T=t_i+1-t_i=t_i+2-t_i+1 – период дискретности.                                                                                                                

Из (1) вытекает формула одного шага ЧИ методом Симпсона:

,                                               (2)

откуда находим передаточную функцию интегратора:

.                                                                                          (3)

Для ограничения выходного сигнала такого интегратора можно предложить детализированную структурную модель, представленную на рис. 1. Блоки Limited Unit Delay в этой структуре представляют собой замаскированные подсистемы, развернутая модель которых изображена на рис. 2. Соотношения уровней ограничения этих блоков и блока Saturation в модели рис.1 имеют вид:

y_{Del Обм}=y_{Sat Обм}/8,       y_{Del Обм}=y_{Sat Обм}/2.                                                                                                                  (4)

В управляемых ключах Switch і Switch1 модели рис. 2 значения u_T параметра Threshold должно удовлетворять условию 0<u_T<1.

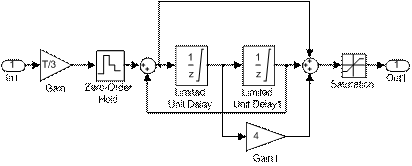
Рисунок 1. Детализированная структурная модель дискретного интегратора второго порядка

с ограничением выходного сигнала

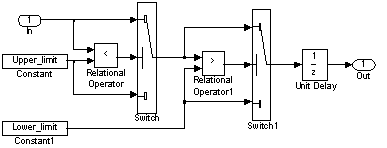
Рисунок 4. Модель блока запаздывания на период дискретности с ограничением выходного сигнала