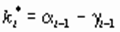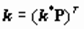Материал взят с сайта:matlab.exponenta.ru
Автоматизация синтеза регуляторов и наблюдателей состояния в среде MATLAB
Толочко О.И., Федоряк Р.В
Донецкий государственный технический университет, г. Донецк, Украина
Синтез регуляторов состояния (РС) и наблюдателей состояния (НС) является весьма трудоемкой задачей, решение которой можно упростить, используя современное программное обеспечение, предназначенное для автоматизации математических и научных расчетов, например, пакеты Mathematica, Mathcad, MATLAB, Maple. Система программирования MATLAB обладает определёнными преимуществами перед своими конкурентами, предоставляя исследователю набор инструментов для синтеза систем автоматического управления Control System Toolbox и систему структурного моделирования Simulink. Однако с нашей точки зрения, наличия всего лишь двух функций acker и place, позволяющих рассчитать коэффициенты РС или НС (причём только в численном виде), крайне недостаточно. Целью данной статьи является разработка методики синтеза регуляторов и наблюдателей состояния полного порядка в численной и в аналитической формах в среде пакета MATLAB.
Синтез РС и НС состоит в выборе коэффициентов корректирующих обратных связей K и L соответственно, из условия обеспечения желаемого распределения полюсов или, что одно и то же, желаемых коэффициентов характеристического полинома замкнутой САУ с РС или замкнутого НС.
При описании алгоритмов мы будем рассматривать четыре основных способа:
1. Алгоритм, основанный на составлении и решении системы n линейных алгебраических уравнений с n неизвестными относительно искомых коэффициентов. В матричной трактовке необходимо решить уравнение
det(pI - A3) = Gж(p),
где A3 - матрица состояния замкнутой системы, которая определяется для САУ с РС и НС как
A3 = A - BK, A3 = A - LC;
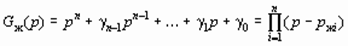 - желаемый полином замкнутой системы.
- желаемый полином замкнутой системы.
2. Алгоритмы расчета, использующие входящие в состав MATLAB функции. Это способ, основанный на использовании формулы Аккермана [1], и один из численных методов, предложенный в [2]. В соответствии с формулой Аккермана искомые коэффициенты можно определить из последней строки матрицы
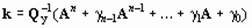
,
3. Алгоритм, описанный в [3] и основанный на использовании формул:
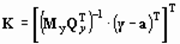
,
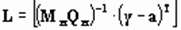
,
4. Алгоритм вычислений с использованием перехода к описанию объекта в канонической форме фазовой переменной [3]. Искомые коэффициенты в каноническом базисе определяются как
а затем переход в исходный базис осуществляется с помощью матрицы перехода Р:
Литература
1. Kailath, T. Linear Systems. Prentice-Hall. 1980.
2. Kautsky, Nichols, Van Dooren. Robust Pole Assignment in Linear State Feedback // Intl. J. Control, 41(1985)5. Р. 1129-1155.
3. Куо Б. Теория и проектирование цифровых систем управления. М.: Машиностроение, 1986. 448 с.



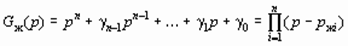 - желаемый полином замкнутой системы.
- желаемый полином замкнутой системы.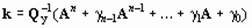 ,
,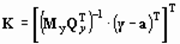 ,
, 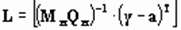 ,
,