Інженер. Студентський науково-технічний журнал. - Донецьк, ДонНТУ, 2005 №6, с.48-51.

ОПРЕДЕЛЕНИЕ ЖЕСТКОСТЕЙ И МОМЕНТОВ ИНЕРЦИИ МНОГОМАССОВОЙ НЕРАЗВЕТВЛЕННОЙ СИСТЕМЫ ПО МИНИМУМУ НАГРУЗОК В УПРУГИХ ЭЛЕМЕНТАХ

Хоменко В.Н., студент; Борисенко В.Ф., проф., к.т.н. (Донецкий национальный технический университет, г. Донецк, Украина)

Современные уникальные машины и агрегаты в большинстве случаев для исследования динамики систем приводятся к n-массовой системе с одним-двумя разветвлениями. Эти разветвления имеют, в общем случае, одинаковые характеристические величины (жесткость, зазор, момент инерции), что позволяет сделать упрощения и свести их к неразветвленной схеме.

Рисунок 1 – Расчетная n-массовая неразветвленная схема

Известно, что минимум нагрузок в упругих элементах электромеханической системы будет иметь место при выполнении следующего соотношения между соответствующими частотами колебания системы:

Omega_(n-1),n = (n-1)*Omega₁₂

где
    n – число расчетных масс системы;
    (n-1) – число упругих элементов в системе;
    Omega₁₂ – собственная частота колебаний двухмассовой системы.

Выражение для Omega₁₂:

Omega₁₂ = sqrt(C₁₂*(J₁+J₂)/(J₁*J₂))

является базовым и в дальнейшем используется для определения Omega₂₃, Omega₃₄, ..., Omega_(n-1),n.

Нахождение величины Omega₁₂ возможно при заданных C₁₂, J₁, J₂.

Нахождение оставшихся величин Omega₂₃, Omega₃₄, .., Omega_(n-1),n не вызывает труда, если заданы жесткости связей и расчетные массы.

Нами в настоящей статье ставится задача более широко: по заданным C₁₂, C₂₃, ..., C_(n-1),n, фиксированной величине Omega₁₂, определить вторые массы двухмассовых блоков (J₂ для системы m₁-m₂, J₃ для системы m₂-m₃ и т.д.). И наоборот, по заданным J₂, J₃, ..., J_n, фиксированной величине Omega₁₂, определить необходимые по условию минимума динамических нагрузок в упругих элементах жесткости (C₁₂ для системы m₁-m₂, C₂₃ для системы m₂-m₃ и т.д.).

В этом случае появляется возможность разработать такую программу расчета, которая будет учитывать оптимальные соотношения между Omega₁₂ и Omega_(n-1),n.

В качестве начальных значений для Omega₁₂ принята величина, равная 50 с^-1. Величина момента инерции первой массы – J₁=1 кг*м². Число расчетных масс n=4.

Программа расчета неизвестных величин момента инерции и второй жесткости для оптимальных соотношений между Omega₁₂ и Omega_(n-1),n приведена ниже:

clc,close all,clear all
J₁=1;Om12=50;kolMass=4;
Ngr=100;
c=[inf linspace(50,2000,Ngr-1)];
om=[(1:kolMass)-1]*Om12;
J=ones(kolMass,Ngr)*J₁;
for j=2:kolMass
for i=1:Ngr
J(j,i)=c(i)*J(j-1,i)/(om(j)*om(j)*J(j-1,i)-c(i));
end
end
col={'r','k--','b','c--','m','r--','k','b--','c','m--'}; i=0;
for j=2:kolMass
if (i<10), i=i+1; else i=1; end
plot(c(2:end),J(j,2:end),col{i}),hold on,grid on
end

По результатам расчетов построена трехмерная система, в которой при фиксации двух величин легко находится третья.

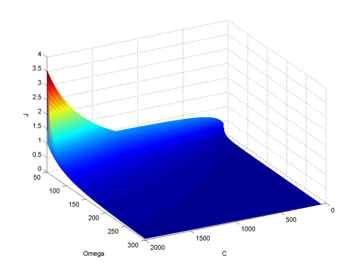
Рисунок 2 – График зависимости (J,C)=f(Omega)

При исключении из графиков Omega₁₂, Omega₂₃, ..., Omega_(n-1),n (рис. 2) можно перейти к плоской системе представления зависимостей (рис. 3).

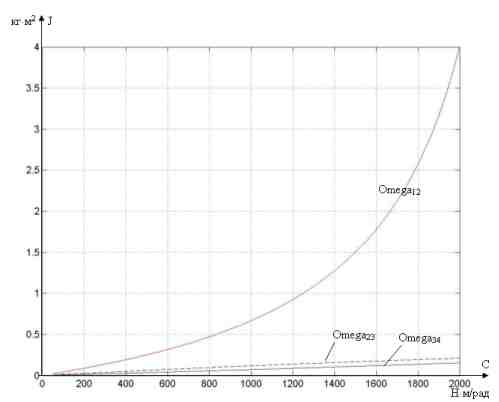
Рисунок 3 – Зависимости J=f(С) для фиксированных значений Omega₁₂, Omega₂₃, ..., Omega_(n-1),n.

Приведем пример определения C₁₂ и J₂ для принятых нами значений величин:

зададимся жесткостью C₁₂=400 Н*м/рад, тогда по кривой Omega₁₂ находим соответствующий момент инерции второй массы J₂=0,19 кг*м². Если C₂₃=1200 Н*м/рад, то для третьей массы J₃=0,138 кг*м². И таким же образом для последующих расчетных масс.

Предлагаемая нами методика может использоваться на этапах раннего проектирования электромеханических систем и служить в качестве диагностирующего признака.