L'arc électrique
Auteurs: Michael Berhanu, Ludovic Blaise-Albospeyre et Jean-Baptiste Michel
1. Définition et conditions d'existence
Il s'agit d'une décharge à forte densité de courant pour laquelle les
processus
thermiques sont dominants. Ils existent pour les conditions suivantes:
- une pression de l'ordre de la pression atmosphérique;
- une intensité de l'ordre de 1A.
Les propriétés thermiques (température du milieu
élevée) et chimiques (conditions idéales pour certaines réactions)
des arcs leur donnent de multiples applications, en particulier dans le secteur de la
métallurgie,
dont on peut citer quelques exemples:
- appareils de coupure
- lampes à arc
- soudure
2. Amorçage d'un arc électrique
Il existe trois grandes méthodes pour amorcer un arc électrique:
Transition continue
Contact
Surtension
2.1 Transition continue
Le système est au départ dans un état de décharge luminescente. La
cathode
est recouverte par le plasma de décharge. Si on augmente l'intensité, la
tension
d'extraction des électrons augmente et la température s'élève. L'émission
thermo-électronique devient majoritaire.
On arrive ainsi, d'une manière continue, à passer d'une décharge luminescente
à un arc électrique.
2.2 Contact
Il est possible (c'est une méthode fréquente), de déclencher
l'arc par contact.
On considère deux pastilles de métal traversées par un courant suffisant.
Lorsque on
les sépare, grâce aux irrégularités de la surface, le courant passe par un
contact très fin; la température s'élève par effet joule jusqu'à la fusion du
métal.On a donc un filet de métal fondu très fin par lequel passe tout le courant.
Lors de la rupture du pont fondu, on est dans les conditions de
formation
d'un arc électrique.
2.3 Surtension
Lorsque la tension dépasse la tension de claquage, une étincelle
apparaît. On
obtient alors un arc par phénomène d'avalanche.
3. Étude а l'anode
La puissance fournie par le circuit et dissipée au
niveau de l'anode peut se décomposer de la manière
suivante :
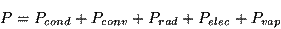
avec :
- Pcond : puissance transmise aux particules par conduction thermique.
- Pconv : puissance de convection du plasma.
- Prad : puissance apportée par rayonnement.
- Pelec : transfert d'enthalpie des électrons vers la cathode.
- Pvap : puissance de vaporisation (comme pour la cathode).
On ne tient pas compte de l'énergie perdue par transferts thermiques
dans
l'anode ni de l'énergie rayonnée.
4. Érosion des électrodes
Les densités de courant ont des valeurs élevées au niveau des
électrodes.
L'énergie est suffisante pour dégrader de manière significative la surface des
électrodes.
Cette érosion est due majoritairement à l'éjection de gouttelettes
de métal fondu (comme on l'a vu, différents processus tels que le bombardement par des ions ou des
électrons font fortement chauffer les électrodes). Il existe des formules empiriques selon les types d'arcs qui
donnent la vitesse de l'érosion des électrodes en fonction de l'intensité dans
le circuit. Dans l'industrie, l'érosion des électrodes impose le remplacement
régulier de celles-ci.
5. L'arc électrique dans un circuit
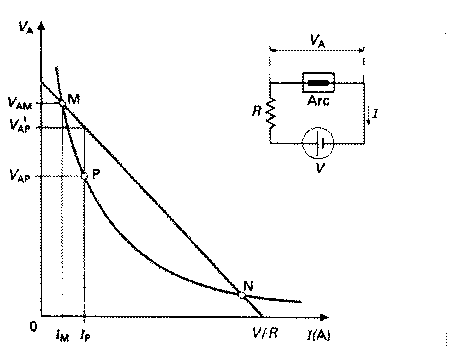
La caractéristique tension - courant d'un arc électrique coupe une
droite de charge
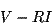 en deux points. Cependant, seul un point est stable, c'est le point
de fonctionnement. On a en effet : en deux points. Cependant, seul un point est stable, c'est le point
de fonctionnement. On a en effet :
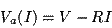 d'où d'où 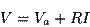
Si le courant passe de I à
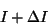 , alors , alors
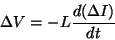 (auto-induction), donc : (auto-induction), donc :
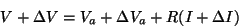
Or on a aussi 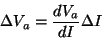 , d'où : , d'où :
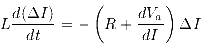
La solution de l'équation est en
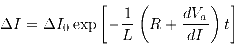
Le retour à la normale dépend donc du signe de 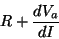 : :
- s'il est positif, une variation de dI entraîne sa diminution au fil du
temps,
donc un retour à la normale.
- s'il est négatif, la même variation entraîne son augmentation.
Il n'y a donc qu'une seule solution stable.
6. Équilibre thermodynamique
Dans un milieu en équilibre thermodynamique, les températures des ions,
des électrons et du gaz neutre sont égales. La distribution des vitesses est celle
de Maxwell, la densité des atomes obéit à la loi de Boltzmann et la densité des
ions, électrons et atomes à la loi de Saha.
À titre informatif, la loi de Saha s'écrit :
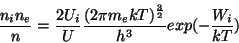
avec ni la densité des ions, ne celle des électrons
(de masse me) et n la densité totale
d'atomes, mais aussi h la constante de Planck, Ui la fonction de partition pour les ions, U la
fonction de partition et Wi l'énergie d'ionisation.
On est conduit, pour étudier la colonne d'arc, à considérer un équilibre
thermodynamique local : c'est-à-dire à prendre en compte des volumes suffisamment
petits pour qu'ils soient en équilibre thermodynamique.
7. Transferts thermiques
Pour établir le profil de température, on doit tenir compte des
transferts thermiques. Les gradients de température et de concentration imposent :
- un flux de particules (diffusion des particules) ;
- un flux d'énergie dI au gradient de température.
Les autres phénomènes sont négligés.
Le transfert thermique obéit а la loi de Fourier.
La conductivité thermique est alors la somme de trois termes:
- la conductivité thermique de translation ;
- la conductivité thermique interne (échanges d'énergie entre les différents
degrés de liberté des molécules) ;
- la conductivité thermique réactionnelle (pour dissocier/associer une molécule).
Ces trois conductivités dépendent de la température. Il en résulte que
la conductivité thermique totale (λ) en dépend aussi.
On peut ainsi obtenir le profil de température dans la colonne (par l'équation
d'Ellenbass-Heller que l'on verra dans la partie suivante).
8. Étude théorique de la colonne d'arc
En combinant, pour un arc considéré а l'équilibre thermodynamique local :
- l'équation de conservation de la masse ;
- l'équation de Navier-Stokes ;
- la loi d'Ohm ;
- la loi de Fourier ;
- la relation d'état des gaz parfaits ;
- un bilan d'énergie ;
- les équations thermodynamiques (Saha et Maxwell) ;
- l'équation de neutralité électrique ;
on arrive а l'équation d'Elenbass-Heller qui donne, pour un arc stabilisé par paroi, sans
vitesse moyenne et gradient de pression :
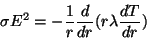
avec r le rayon (symétrie cylindrique), λ la conductivité thermique,
σ la conductivité électrique et E le champ électrique.
Dans cette équation, la puissance rayonnée est négligée. C'est avec
celle-ci
qu'on arrive à déterminer l'expression de la température T en fonction de r.
C'est une équation difficile à résoudre puisque les conductivités thermique
et électrique sont des fonctions complexes de la température. Sa résolution
se fait donc numériquement.
9. Extinction de l'arc
Quand on annule le champ électrique entre les électrodes, le courant
disparaît,
mais le plasma subsiste encore quelque temps. Le temps de subsistance dépend de
la vitesse de recombinaison électrons - ions et du refroidissement du gaz.
Au départ, on suppose que toutes les particules sont à la même température.
Un bilan d'enthalpie donne, au final, (en supposant 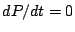 ,
c'est-à-dire que la pression ne varie pas dans le temps) l'équation : ,
c'est-à-dire que la pression ne varie pas dans le temps) l'équation :
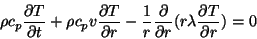
avec: ρ la masse volumique, cp la capacité calorifique а pression constante,
v la vitesse des particules et λ la conductivité thermique.
On peut résoudre cette équation numériquement
pour obtenir les variations de T(t). Les résultats obtenus sont en parfait accord
avec les études expérimentales.
Source >>
|