Статья подготовлена для сборника ДонНТУ.
МОДЕЛИРОВАНИЕ ОЧАГОВОГО ЗАЖИГАНИЯ ВЗРЫВООПАСНОЙ ГАЗОВОЙ СМЕСИ С УЧЕТОМ ЗАДАННОЙ
МОЩНОСТИ ТЕПЛОВЫХ ИСТОЧНИКОВ ИСКРОВОГО РАЗРЯДА
И.А.Бершадский, М.С.Клименко
ДонНТУ, кафедра «Электроснабжения предприятий и городов»
Актуальность проблемы. Одним из направлений повышения безопасности труда при
эксплуатации электрооборудования во взрывоопасных средах является широкое применение
искробезопасных систем. Искробезопасное исполнение основано на том факте, что электрические
разряды малой энергии оказываются неспособными воспламенить взрывчатую смесь. К области его
применения относятся слаботочные системы, аппаратура и приборы автоматики, связи, измерений,
контроля и т.д.
Однако, до настоящего времени в недостаточной степени разработаны методы расчетной оценки
искробезопасность электрических цепей, что существенно затрудняет выбор оптимальных вариантов
искробезопасной аппаратуры, усложняет их испытание и конструирование.
Количественная оценка условий воспламенения может быть дана только на основе управления
зависимостей (аналитических или численных (моделируемых)) многообразных факторов, влияющих на
процессы искрообразования и последующего зажигания смеси. Например, в указывается, что условия
взрыва газа от электрической искры зависит от характера изменения и величины I, U, P, Wp,
размеров, материала, формы, скорости расхождения контактов; параметров смеси, ее
теплофизических свойств и движения в момент воздействия разряда.
Постановка задачи и принятые допущения.Анализ ряда литературных источников показал
взаимосвязь, существующую между тепловым действием энергии электрического разряда и
воспламенением газовой смеси. Согласно тепловой теории весь газ может быть воспламенен,
если определенный (эквивалентный) сферический объем радиуса Rэвк будет нагрет до
температуры воспламенения (Твосп = 2100К для 8.62% метановоздушной смеси).
Воздействие такого источника на ВС сводится к ее нагреву, развитию ядра пламени, а затем к
достижению этим ядром пламени некоторых минимальных размеров, при которых реакция горения
становится самоподдерживающейся. Тогда весь окружающий разряд взрывчатый газ воспламенится,
если даже источник поджигания прекратит существование.
Математическая модель электрического зажигания взрывоопасной атмосферы, следовательно,
должна представлять систему уравнений в рамках тепловой теории зажигания, описывающую процессы
теплопроводности, химической кинетики, а также учитывающую связь между значениями
относительной концентрации горючего в любой точке пространства и значениями температур в этих
точках, и содержащую внутренние источники тепла в столбе разряда.
Ввиду необходимости учета большого количества факторов, введем ряд упрощений и допущений:
1.Пренебрегаем влиянием электродов (достаточно быстро размыкающаяся цепь);
2.Считаем, что в областях, не занятых искрой, тепловые свойства газовой смеси подчиняются
аппроксимирующим зависимостям, полученным по данным;
3.Распределение температуры определяется решением нестандартного уравнения теплопроводности в
сферических координатах;
4.Дуговой столб имеет цилиндрическую форму, а температура по радиусу столба изменяется в
соответствии с рассчитанной по «методу источников»;
5.При скорости движения пламени менее скорости звука можно пренебречь зависимостями параметров
газовой смеси от давления.
Изложение основного материала исследований. Для разработки модели электрического зажигания
газовой смеси применяется уравнение (1) с тепловыми источниками в виде эквивалентной мощности,
выделяющейся при экзотермической реакции (Q), а также электрического разряда, заданной
тепловой мощностью на единицу объема Р0:
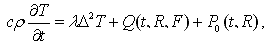 (1)
(1)
где с [Дж/кг*К], &rho [кг/мм3] – теплоемкость и плотность газовой смеси; &lambda
[Вт/мм*К] – коэффициент теплопроводности; Q – мощность теплового источника экзотермической
реакции; Р0 [Вт/мм3]– мощность искрового разряда; R – сферическая
координата; Т [К]– мгновенное значение температуры в момент времени t [мкс]; F - доля
выгоревшего металла по отношению к его нормальной концентрации.
Рассмотрим кинетику химической реакции горения метановоздушной смеси. Известно, что в
качестве основного постулата химической кинетики принято положение, что скорость реакции
пропорциональна произведению концентрации реагирующих веществ в данный момент времени. Для
случая бимолекулярной реакции:
 (2)
(2)
где W – скорость реакции, [молекул/см3*сек]; nA, nB –
количество молекул веществ A и B в 1см3; –
средний эффективный диаметр сталкивающихся молекул, см; –
средний эффективный диаметр сталкивающихся молекул, см; 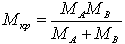 – приведенный молекулярный вес; p=1 – вероятностный коэффициент; Е – энергия активации,
[кал/моль]; R=1.987, [кал/моль*К].
– приведенный молекулярный вес; p=1 – вероятностный коэффициент; Е – энергия активации,
[кал/моль]; R=1.987, [кал/моль*К].
Если концентрация компонента Ci выражается в [г-моль/л], то получим
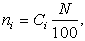 N=6.02*1026. В результате для W имеем: N=6.02*1026. В результате для W имеем:
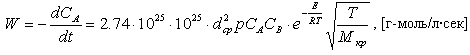 (3)
(3)
Константа “Е” в данной газовой смеси принимается по рекомендации.
Количество тепла, выделяющегося в единице объема: [г-моль/мм3*сек]
Q=q*w
где q=889.5*103 Дж/моль – удельная тепловая способность реакции.
В выражении (3) необходимо учесть выгорание в процессе реакции реагирующих компонентов и,
следовательно, уменьшение их концентрации. При этом, исходя из уравнения реакции
CH4 + 202 = 2H2O + CO2, текущая концентрация
метана составит CA=C1-FC1, а кислорода
CB=C2-2*FC1 (C1 и C2 – начальные
концентрации метана и кислорода).
Количество тепла, выделяющееся в m-й точке в k-тый момент времени зависит от доли
выгоревшего компонента fm,k, на (k-1)-ом шаге по времени в m-той точке:
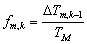 (4)
где ТМ – температура при полном сгорании компонента.
(4)
где ТМ – температура при полном сгорании компонента.
Суммарная доля сгоревшего компонента в m-той точке k-того шага по времени может быть
найдена путем последовательного суммирования:
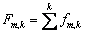 (5)
(5)
Моделирование зажигания газовой смеси должно учитывать, что на развитие очага влияет
характер распределения температур в стволе разряда при заданной мощности Р0.
Предварительные исследования различных моделей для расчета температуры электрической дуги
показали, что удовлетворительные результаты могут быть получены приближением к цилиндрической
форме столба дуги. Отвод теплоты внутри столба осуществляется лишь теплопроводностью. Затем
применим “метод источников”, предполагающий линейность уравнений (считая, что тепловые
параметры дугового газа - неизменны).
Далее искровой разряд заменяется непрерывным линейным источником тепла мощностью Р0 ,
действующим, начиная с момента времени t'=0 до t'=t. Данный источник вносит в элемент объема
в виде бесконечной длинной призмы с основанием dxdy и осью, расположенной параллельно оси z,
количество тепла Q1 на единицу длины. Температура элемента повысится на
Q1/c&rhodxdy. Распространение теплоты от линейного источника представляем в виде
наложенных процессов бесконечного количества точечных источников, распределенных по оси z и
вносящих элементарные количества теплоты dQ=Q1dz.
Для неограниченного тела нестационарному уравнению теплопроводности удовлетворяет решение:
 (6)
где r =
(6)
где r =  - сферический радиус-вектор; с – удельная теплоемкость газа; а – коэффициент температуропроводности. - сферический радиус-вектор; с – удельная теплоемкость газа; а – коэффициент температуропроводности.
(6) представляет решения уравнения теплопроводности для мгновенного точечного источника
теплоты. Согласно принципу наложения, решение уравнения нестационарной теплопроводности:
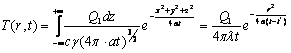 (7)
(7)
(7) является решением для условий нагрева мгновенным линейным источником, процесс
распространения тепла от непрерывного действующего источника на расстоянии r от оси для
выделяемого в единицу времени количества теплоты Р0 определяется по методу
наложения:
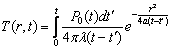 (8)
где t – суммарное время действующего источника; t' - текущее время.
(8)
где t – суммарное время действующего источника; t' - текущее время.
Если мощность искры неизменна во времени (Р0=const), тогда решение (8)
запишется в виде:
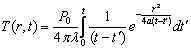 (9)
(9)
Выражение (9) вычислялось методами приближенного интегрирования в пакете MathCad12, и
формулировалось семейство температурных зависимостей при различных мощностях Р0=0.5;1.5;… Вт.
Предельный критический радиус цилиндрического дугового столба Rd определялся как граница, за
пределами которой T(r,t)≤300К.
Приняв во внимание рассмотренные свойства источником теплоты в уравнении (1), рассмотрим
алгоритм, реализующий на ЭВМ модель зажигания метановоздушной смеси от маломощного искрового
разряда. Укрупненная блок-схема приведена на рис.1.
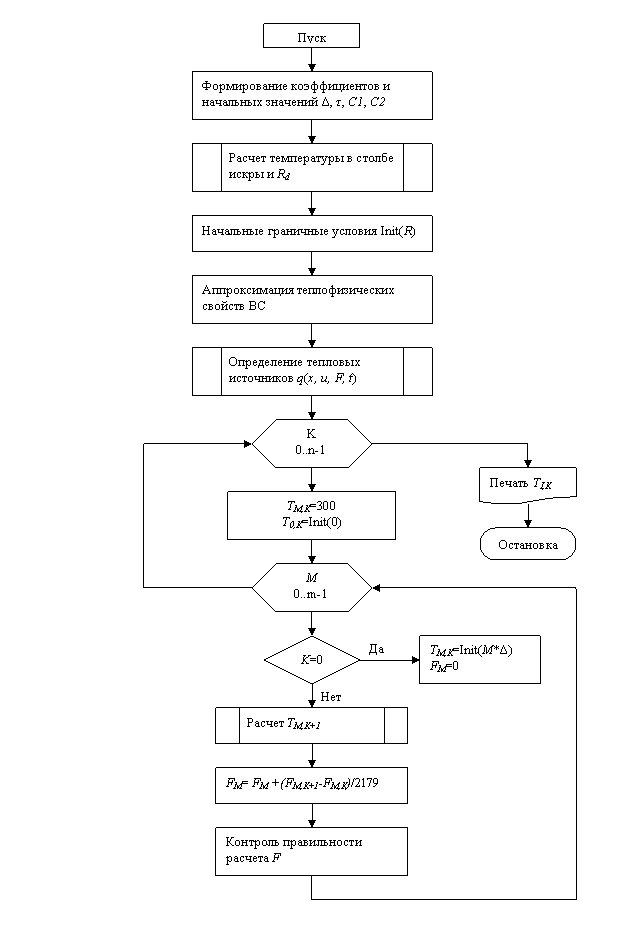 Рисунок 1 - Блок-схема, реализующий модель зажигания метановоздушной смеси от
маломощного искрового разряда.
Рисунок 1 - Блок-схема, реализующий модель зажигания метановоздушной смеси от
маломощного искрового разряда.
Использовалась следующая явная 4-х точечная разностная схема для уравнения теплопроводности:
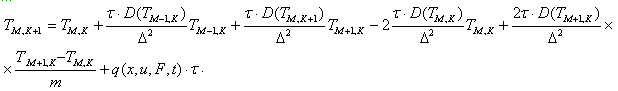 (10)
где D – коэффициент температуропроводности; Q – функция источника, учитывающая одновременное
выделение тепла в экзотермической реакции и плазме дуги.
(10)
где D – коэффициент температуропроводности; Q – функция источника, учитывающая одновременное
выделение тепла в экзотермической реакции и плазме дуги.
Следует отметить недостаток рассмотренной явной разностной схемы из-за неустойчивости, в
некоторых случаях, решения, которое проявляется в колебательном характере зависимости Т(t).
|