"Журнал технической физики", 1964, вып.5, с.492.

Проведено приближенное решение уравнения энергетического баланса столба дуги, позволяющее рассчитать основные параметры столба, если известен состав дуговой плазмы. На основе полученных соотношений предложено объяснение факта независимости форм радиального распределения теплопроводности в столбе дуги от силы тока и состава дуговой плазмы. Полученные результаты могут оказаться полезными при исследованиях в области спектрального анализа электросварки, а также при изучении свойств низкотемпературной плазмы.

1. Основные параметры столба электрической дуги, горящей в условиях естественной конвекции, могут быть установлены теоретическим путем, если, во-первых, характеристики плазмы (электропроводность, теплопроводность и др.) являются известными величинами для температур, имеющих место в дуговом разряде, и, во-вторых, оказывается возможным решить систему уравнений, одно из которых представляет собой баланс энергии для единицы объема дуговой плазмы.

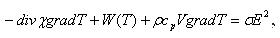     (1)

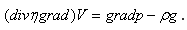     (2)

Здесь Т и V — температура и скорость движения плазмы в некоторой точке пространства; σ, χ, η, с_р и ρ — электропроводность, теплопроводность, вязкость, удельная теплоемкость и плотность плазмы, являющиеся функциями от Т; Е — напряженность электрического поля; W - энергия, отводимая из единицы объема плазмы посредством излучения, g — ускорение свободного падения.

Детальное рассмотрение свойств плазмы является задачей кинетической теории материи и выходит за рамки настоящей работы. В дальнейшем предполагается, что все используемые параметры плазмы являются известными функциями температуры. Решение системы уравнений (1), (2) наталкивается на значительные математические трудности, что вынудило занимавшихся этим вопросом исследователей делать упрощающие задачу предположения. Так, Ламар и Стоун заменяли &rhoс_рVgradT, отображающий конвективный вынос тепла, особым образом сконструированной функцией от Т (но не содержащей V) и решали в численной форме только уравнение (1). Чемпион, напротив, считал известным вид радиального распределения температуры Т(r) и решал только уравнение (2). Недостатком обоих способов решения является расчет произвольных функций, что придает им чисто описательный характер.

Предполагаемый в настоящей работе подход к решению проблемы основан на оценке относительной роли ответственных за преобразование и перенос энергии процессов в энергетическом балансе различных температурных областей дуги и вытекающей отсюда возможности подразделение разряда на ряд зон, в пределах каждой из которых можно пренебречь тем или иным процессом.

Излучение плазмы при атмосферном давлении составляет лишь небольшой процент от энергии, преобразуемой в дуге, так как даже при очень высоких температурах плотность плазмы убывает столь быстро, что доля излучения остается малой. Расчеты Пельцера для дуги показывают, что даже при силе тока порядка сотен ампер потери на излучение не превышают 20% от полной мощности разряда. Эксперименты с угольной дугой в воздухе также говорят о малой роли излучения. Поэтому для упрощения расчетов можно принять W(T)=0.

Распределение электрической мощности σЕ² по сечению дуги определяется исключительно радиальным распределением электропроводности, так как продольный градиент поля Е в пределах проводящей части практически постоянен. Учитывая, что электропроводность плазмы резко падает с уменьшением температуры, с достаточной степенью точности можно принять σ = 0 при Т≤Т1. О критерии для выбора величины Т1 будет сказано ниже.

Конвективный теплоотвод, представленный в уравнении (1) членом VgradT практически отсутствует в центральных зонах дуги. Это объясняется, во-первых, малой плотностью газа при высоких температурах Это объясняется, во-первых, малой плотностью газа при высоких температурах (ρ∼1/T) и, во-вторых, тем, что, как показывает эксперимент, в центральных частях дугового разряда изотермические поверхности и направление скорости восходящих газовых потоков приблизительно параллельны оси столба (а следовательно, и друг другу). Поэтому можно считать, что при температурах, превышающих некоторую величину Т₂, конвективный теплоотвод вообще отсутствует. Нужно отметить, что Т₂ возможно определить теоретически, так как для этого потребовалось решить систему уравнений (1), (2). Поэтому при выборе конкретного значения Т₂ можно основываться только на экспериментальных данных температурного поля и поля газового потока в столбе дуги, которых, к сожалению, весьма мало. Положение облегчается тем, что особой точности в установлении Т₂ не требуется. Проведенные расчеты показывают, что уменьшение или увеличение Т₂ на 500ºК мало сказывается на окончательных результатах вычислений. Кроме того, установлено, что при увеличении силы тока на порядок значение температуры Т₂ практически остается постоянным.

На основании вышеизложенного представляется естественным разделением всей области, занимаемой столбом дуги, на следующие три зоны.

Проводящая зона (I). В ее пределах происходит выброс электрической энергии, которая посредством теплопроводности переходит во внешние части дуги. Зона простирается от оси дуг до изотермической поверхности Т₁.

Нейтральная зона (II). Концентрация электронов о ионов по сравнению с зоной I пренебрежимо мала. Теплоотвод за счет теплопроводности. Зона ограничена изотермическими поверхностями Т₁, и Т₂ (Т₁ >Т₂).

Зона конвекции (III). Источники энергии отсутствуют. Теплоотвод посредством теплопроводности и конвекции. В пределах зоны происходит спад температур от Т₂ до Т_вн, где Т_вн — температура окружающей среды.

Так как в пределах двух внутренних зон изотермические поверхности и направление скорости газового потока параллельны оси дуги, то значение температуры в любой точке этих зон однозначно определяется расстоянием от оси. Принимая также во внимание, что продольный градиент поля Е почти не меняется вдоль столба дуги (конечное за исключением областей катодного и анодного падения потенциала), уравнение для внутренних зон можно записать в виде

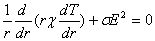     (3)

В этом уравнении не содержится каких-либо величин, зависящих от скорости газового потока, что позволяет решить его (с точностью постоянной интегрирования) независимо от гидродинамического уравнения (2). Одно из граничных условий для уравнения (3) вытекает из цилиндрической симметрии столба и имеет вид

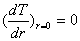     (4)

Трудности возникают при отыскании граничного условия верхнего края второй зоны. При строгом решении задачи оно представляет собой требование равенства на границе между зонами II и III функции Т(r) и ее первой производной, вычисленных по уравнениям соответствующим зонам II и III. Однако определение температурного деления в пределах зоны III обязательно требует решения гидродинамического уравнения (2), что не представляется возможным. Преодолеть возникшее затруднение, как нам кажется, можно следующим образом. Отказавшись от определения температурного поля и поля скоростей в пределах зоны III, рассмотрим теплообмен между внешней поверхностью плазменного цилиндра радиуса r₂ (где r₂=r_T=T2) и окружающей среды на основе полуэмпирических соотношений теории теплообмена теплового потока с единицы поверхности температуры Т₂ твердого цилиндра указанная теория в случае свободной конвекции турбулентного характера дает следующую формулу

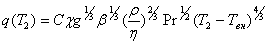     (5)

где χ, η, ρ, β и Р_Г — теплопроводность, динамическая вязкость, плотность, коэффициент объемного расширения и критерий Прандтля, отнесенные к температуре 1/2(Т₂+Т_вн); С — постоянная, не зависящая от свойств газа, в котором наблюдается конвекция. Как было показано, соотношение (5) оказывается пригодным и для описания конвективного теплоотвода от столба дуги, однако с другим значением С. Граничным условием для внешней поверхности зоны II может служить равенство

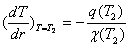     (6)

Так как коэффициент теплопроводности плазмы является сложной функцией температуры, то для решения уравнения (3) полезно ввести, согласно Айресу и другим, функцию теплопроводности

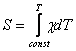
Так впервые была использована в теории дуги Шмитцем. В нашем случае в качестве нижнего предела интегрирования удобно принять Т₂, так что

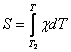     (7)

Заменяя в уравнении (3) с помощью соотношения (7) Т через S, получим

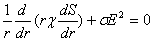     (8)

граничные условия (4) и (6) примут вид

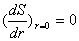     (9)

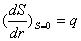     (10)

Входящая в уравнение (8) электропроводность плазмы σ рассматривается как функция от S и легко может быть рассчитана если известно χ(Т).