"Журнал технической физики", 1965, вып.1, с.89.
К ТЕОРИИ ВОЛЬТАМПЕРНОЙ ХАРАКТЕРИСТИКИ СТОЛБА НЕСТАЦИОНАРНОГО ДУГОВОГО РАЗРЯДА
ВЫСОКОГО ДАВЛЕНИЯ
Крижанский С.М.
Получено приближенное уравнение динамической вольтамперной характеристики столба
нестационарного дугового разряда высокого давления. Решение проведено при аппроксимации
функций, характеризующих свойства среды, единой для всего интервала изменения температуры
по радиусу разрядной трубы. Показана возможность построения метода последовательных
приближений для решения задачи о зависимости температуры в столбе от радиуса и времени, а
также для уточнения динамической вольтамперной характеристики.
Процессы изменения во времени напряжения на дуге и тока дуги, горящей между контактами
выключателя, зависят как от параметров внешней электрической цепи, элементом которой является
дуговой промежуток, так и от условий, имеющих место в самом дуговом промежутке. Внешняя
электрическая цепь полностью характеризуется соответствующим обыкновенным дифференциальным
уравнением или системой таких уравнений, методы составления которой хорошо известны.
Нахождение уравнения, связывающего ток и напряжение дугового промежутка (называемого
вольтамперной характеристикой разряда), для дуг постоянного тока, так и в особенности для
дуги переменного тока, представляет большие трудности. Такое уравнение невозможно получить
без рассмотрения тепловых процессов, протекающих в столбе дугового разряда.
В настоящей работе рассматриваются лишь такие стадии горения электрической дуги
переменного тока высокого давления, в течение которых процессы в дуговом промежутке
определяются энергетическим балансом.
Рассмотрим столб дугового разряда, стабилизированный стенкой в случае цилиндрической
симметрии. Конвекционный перенос энергии в однородном по длине столбе
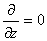 отсутствует. Ограничиваясь рассмотрением медленных
(по сравнению со скоростью звука) движений газовой среды пренебрежем механической инерцией
плазмы. Это приводит к постоянству давления по сечению разрядной трубки. Если объем
разрядного промежутка свободно сообщается с атмосферой, то давление будет постоянно и во
времени. Пренебрегая, кроме того, макроскопическим движением плазмы в радиальном направлении,
можно записать уравнение теплового баланса в следующем виде отсутствует. Ограничиваясь рассмотрением медленных
(по сравнению со скоростью звука) движений газовой среды пренебрежем механической инерцией
плазмы. Это приводит к постоянству давления по сечению разрядной трубки. Если объем
разрядного промежутка свободно сообщается с атмосферой, то давление будет постоянно и во
времени. Пренебрегая, кроме того, макроскопическим движением плазмы в радиальном направлении,
можно записать уравнение теплового баланса в следующем виде
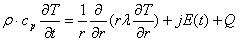 (1)
(1)
Здесь j=σE —плотность тока; Е(t) — поле однородное по сечения разрядной трубки;
Т(r,t) — температура; ρ, ср, λ и σ — соответственно плотность,
теплоемкость при постоянном давлении, теплопроводность, электропроводность газовой среды;
Q — потери на излучение на единицу объема плазмы. Зависимость последних пяти величин от
температуры и давления предполагается известной.
Вид граничных условии зависит от интенсивности охлаждения трубки. Если охлаждение
осуществляется вследствие обтекания естественными конвекными потоками, то можно принять при
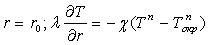 (2)
(2)
Здесь Токр — температура окружающей трубку среды. Показатель n при умеренных
температурах стенки и охлаждении ее воздухом близок к 3/2 и растет с увеличением температуры
стенки. Коэффициент теплоотдачи χ увеличивается с ростом интенсивности охлаждения
(например, водой) и в пределе 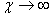 . При этом условие (2)
переходит в условие постоянства температуры на стенке . При этом условие (2)
переходит в условие постоянства температуры на стенке
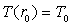 (3)Граничное условие вида (3) будет применяться при всех дальнейших выкладках. Однако они
могут быть обобщены и на граничное условие вида(2).
(3)Граничное условие вида (3) будет применяться при всех дальнейших выкладках. Однако они
могут быть обобщены и на граничное условие вида(2).
Основную трудность при интегрировании уравнения (1) представляет нелинейность зависимостей
величин ρср, λ, σ и Q от температуры. Для преодоления этой
трудности в теории стационарного разряда Шмитц и Меккер предложили ввести новую функцию
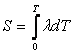 . По аналогии с S можно ввести функцию . По аналогии с S можно ввести функцию
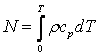 . При этом уравнение (1) преобразуется к виду . При этом уравнение (1) преобразуется к виду
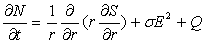 (4)
(4)
В стационарном случае (при Q = 0) Меккер воспользовался далее кусочно-линейной
аппроксимацией функции σ(S). Он разделил промежуток (0 — r0) на два,
считая, что ток протекает только в центральной части, а в оболочке σ = 0. При этом
граница токопроводящей части канала являлась функцией полного тока. Однако ввиду грубости
кусочно-линейной двучленной аппроксимации, принятой Меккером, для обеспечения
удовлетворительной точности для каждого значения тока необходимо находить свою аппроксимацию
функции σ(S). Увеличение числа отрезков аппроксимации приводит к появлению в решении
не одного, а нескольких подвижных радиусов, являющихся функцией тока, что значительно
усложняет решение. Отмеченные трудности усугубляются в теории дуги переменного тока, когда
все величины меняются во времени. В этом случае точность при кусочно-линейной аппроксимации
особенно понижается для области малых токов вблизи перехода тока через нулевое значение.
Фринд применил метод кусочно-линейной аппроксимации в нестационарном случае, однако не учел,
что граница между токопроводящей зоной и оболочкой, где σ = 0, является в этом случае
функцией времени. Использованный Фриндом метод разделения переменных невозможно применить к
задаче с подвижной границей.
Учитывая вышеизложенное, в настоящей работе вводятся аппроксимации функций, входящих в
уравнение (4), выраженные единой формулой на всем интервале их изменения.
Полный ток, протекающий через столб дуги, определяется интегралом от электропроводности
по сечению разрядной трубки
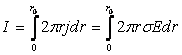 (5)
(5)
Поле Е(t) предполагается постоянным по сечению. Уравнение, связывающее эти две величины,
характеризует дуговой разряд также интегрально. Поэтому для вывода вольтамперной
характеристики нет необходимости в детальном знании законов изменения температуры по радиусу.
Это позволяет существенно упростить задачу. Будем отыскивать приближенное решение уравнения
(4), которое вместо точного удовлетворения ему в любой точке промежутка будет удовлетворять
этому уравнению лишь в среднем на всем интервале изменения координаты r.
Для получения такого приближенного решения усредним уравнение (4) по радиусу с весом r.
Умножая (4) на 2πrdr и интегрируя по r от нуля до стенки трубы r0, получим
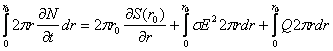 (6)
(6)
Воспользовавшись определением полного тока (5) и поменяв местами знаки интеграла и
производной по времени, получим
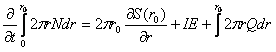 (7)
(7)
Искомое приближенное решение должно удовлетворять уравнению (7), характеризующему
интегральный энергетический баланс единицы длины дугового столба. Представив N, S и Q как
функции тока и поля, получим также уравнение вольтамперной характеристики.
Выразим в явном виде три из входящих в уравнение (4) функции через четвертую, исключив тем
самым из рассмотрения температуру. Выберем в качестве неизвестной функции S(r,t), так как в
этом случае пространственный дифференциальный оператор, входящий в уравнение (4), сохраняется
линейным.
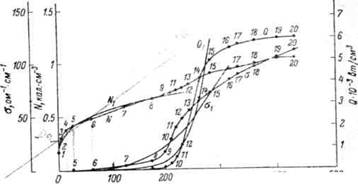
На рисунке приведены зависимости σ(S), N(S) и Q(S) для воздуха или азота при
атмосферном давлении. Цифры на кривых указывают температуру в тысячах градусов Кельвина для
соответствующих точек. Кривые построены по данным для теплоемкости и плотности воздуха, для
теплопроводности азота, для электропроводности воздуха и для интегральных потерь на
излучение азота за счет непрерывного спектра. (Излучение в линиях при давлениях порядка
атмосферного благодаря узости линий дает незначительный вклад в общую величину потерь на
излучение). Характер изменения этих величин весьма сложен и обычно соответствующие функции
могут быть заданы лишь численно.
Функции σ(S) и Q(S) в общем случае можно аппроксимировать алгебраическими полиномами
с целыми показателями степени
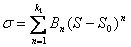 (8)
(8)
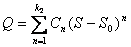 (9)
где S0 соответствует Т0.
(9)
где S0 соответствует Т0.
Такой вид аппроксимации удобен для решения как стационарной, так и нестационарной задач.
Количество членов, необходимых для получения нужной точности, зависит от максимального тока
дуги, рассматриваемого в задаче, и соответствующей этому току температуре центре дугового
столба. Величину температуры в центре можно оценить из решения более простой стационарной
задачи. Если ограничиться не слишком высокими температурами, то удовлетворительную точность
можно получить с помощью одночленной степенной аппроксимации (показатель степени при этом не
обязательно должен быть целым)
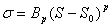 (8')
(8')
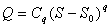 (9')
(9')
На рисунке приведены для иллюстрации соответствующие кривые
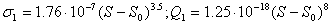
Функция N(S) для данных рисунка хорошо аппроксимируется (до ~ 12000ºК)
иррациональной функцией вида
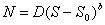 (10)
(10)
где b=0.25; D = 0.18. Для других газовых сред эта функция сохраняет иррациональный
характер и может быть аппроксимирована следующим образом
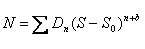 (11)
(11)
Для N(S) также может быть применена аппроксимация полиномом с целыми показателями, но
иррациональный характер этой функции потребует применения многочлена высокой степени. В то же
время аппроксимация ее главной части, начиная с Т ~ 4000ºК, может быть хорошо
произведена прямой. Для некоторых случаев удобно аппроксимировать N(S) прямой на всем
интервале изменения S, хотя это и приводит к завышению тепловой инерции дуги.
Такая аппроксимация имеет вид
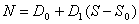 (11')
(11')
Преобразуем уравнение (4) к безразмерному виду, для чего введем новые независимые
переменные и неизвестную функцию
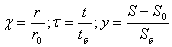 Здесь tб и Sб — базисные величины.
Здесь tб и Sб — базисные величины.
В новых переменных с учетом аппроксимирующих выражений для σ(S), Q(S) и N(S)
уравнение (4) перепишется так
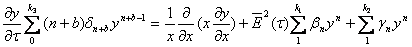 (12)
(12)
с граничным условием y(1)=0 (13)
где обозначено
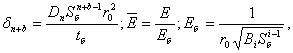
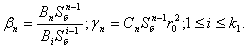 Введем также базисную величину для тока Iб, связанную с Еб и
Sб соотношениями
Введем также базисную величину для тока Iб, связанную с Еб и
Sб соотношениями
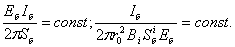 Будем искать приближенное решение тепловой задачи в виде
Будем искать приближенное решение тепловой задачи в виде
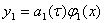 (14)
(14)
где a(τ) — неизвестная функция времени, а φ(х) — известная четная функция,
удовлетворяющая граничному условию (13). Четность решения следует из вида уравнения (12).
За функцию φ(х) можно выбрать подходящий полином или другую функцию из какой-либо
полной системы. Выберем в качестве φ(х) Бесселеву функцию первого рода. Тогда
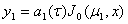 (15)
где μ1 = 2.405 — первый корень уравнения J0(μ1)= 0.
(15)
где μ1 = 2.405 — первый корень уравнения J0(μ1)= 0.
Такой выбор оправдан тем, что J0(μ1,x) является собственной
функцией соответствующей линейной задачи. Кроме того, эта функция удовлетворяет как
граничному условию в точке x=1, так и условию коллокации в этой точке.
Для определения неизвестной функции a1(τ) подставим (15) в (12) и
произведем усреднение аналогично тому, как это в общем виде было показано при получении
уравнения (7). После интегрирования получим, учитывая определение полного тока (5)
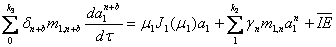 (16)
где
(16)
где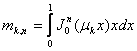
Выразим а1(τ) через проводимость единицы длины дугового столба. Для этого
подставим в (5) выражение σ(S), определяемое (8), в которое в свою очередь подставим
выражение (15) приближенного решения и проинтегрируем. После этих операций получим
алгебраическое уравнение относительно а1(τ)
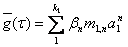 (17)
(17)
где g(τ) — проводимость столба в относительных единицах; aτ— корень уравнения
(17), исчезающий при g→0. Решая (17) относительно aτ(g) каким-либо точным или
приближенным способом, можно исключить aτ из (16). В результате можно получить
обыкновенное дифференциальное уравнение динамической вольтамперной характеристики дугового
разряда.
Это уравнение в общем виде весьма сложно и громоздко, что объясняется сложностью
аппроксимаций функции, характеризующих свойства газовой среды. Здесь приведем частный вид
этого уравнения при одночленных степенных аппроксимациях этих функций (8'), (9') и (10). В
этом случае получаем
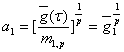 Уравнение вольтамперной характеристики принимает следующий вид
Уравнение вольтамперной характеристики принимает следующий вид
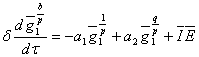 (18)
где
(18)
где 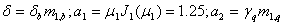
Уравнение (18) содержит две неизвестные функции времени — ток и поле. Их определение
возможно лишь при совместном его решении с уравнением внешней цепи.
Как ясно из вывода уравнения (18), каждый его член обязан своим происхождением
соответствующему члену уравнения энергетического баланса (4). В частности, левая часть
уравнения отражает наличие у столба дугового разряда тепловой инерции, проявляющейся в
гистерезисе динамических вольтамперных характеристик. В случае одночленной аппроксимации
N(S) тепловую инерцию столба дуги характеризует постоянная времени
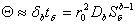 [сек]. Можно показать, что [сек]. Можно показать, что
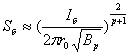 В случае синусоидального тока целесообразно принять Iб=Imах. Тогда
В случае синусоидального тока целесообразно принять Iб=Imах. Тогда
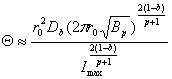
т. е. зависимость постоянной времени от максимального значения тока, определяющего нагрев
газа, падающая. Зависимость постоянной времени от давления замаскирована в коэффициентах
Db, Вр и показателях степени b и р. Для случая аппроксимации N(S) по
формуле (11) невозможно одной постоянной времени характеризовать тепловую инерцию столба дуги.
При аппроксимации N(S) прямой по формуле (11') постоянная времени оказывается независящей от
максимального тока дуги, так как в этом случае b = 1 и Θ ~ r02D1.
При r0=1 см; Θ ~ 6*103 сек. (для данных рисунка). Статическая
характеристика получается из (18), если положить d/dt=0. Уравнение динамической вольтамперной
характеристики дугового разряда высокого давления ранее уже вводилось в рассмотрение. Однако
в этих работах вид уравнения динамической характеристики и особенно его левой части
устанавливался на основании весьма общих и грубых представлений о тепловом балансе столба
дуги. Параметры, входящие в эти уравнения, почти не связывались с реальными характеристиками
газовой среды. Это приводило к тому, что само уравнение носило лишь качественный характер.
Вывод, проведенный в настоящей работе, позволяет однозначно связать вид уравнения
вольтамперной характеристики с основными характеристиками газа — тепло- и электропроводностью
и теплоемкостью, а также излучательной способностью. В частности, метод позволяет установить
зависимость постоянной времени дуги, характеризующей тепловую инерцию дугового столба, от
рода газа и давления. В то же время уравнения (16) и (18) носят приближенный характер.
Как это ясно из формулировки задачи, в уравнении вольтамперной характеристики отражены лишь
радиальные потери энергии и не учтены пота тепла на электроды, т. е. в осевом направлении.
В случае дуг с плавящимся металлическим электродом осевые потери могут быть существенны для
дуг длиной даже в несколько сантиметров. Приближенный характер уравнений определяется
также произвольным выбором вида решения в форме (14) и функции Бесселя в качестве
аппроксимирующей для радиального распределения температуры.
Способ усреднения уравнения (4), примененный для вывода вольтамперной характеристики и
нахождения приближенного решения тепловой задачи, можно рассматривать как первое приближение
в некотором методе последовательных приближений. Если разбить интервал (0-1) на l
подынтервалов и потребовать, чтобы решение удовлетворяло уравнению (4) в среднем на каждом
подынтервале, то получи обыкновенных дифференциальных уравнений для нахождения неизвестных
функций ак (τ) в приближенном решении вида
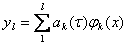 (19)
(19)
Если обозначить правую часть уравнения (4) через L(у), то система обыкновенных уравнений
примет вид
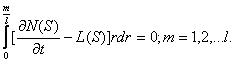 (20)
(20)
Практическое получение системы (20) затруднено, если аппроксимация N(S) выражена
иррациональной функцией. Система при этом пол чается нелинейной относительно производных
ак (τ) по времени. Целее образно использовать в этом случае аппроксимацию N(S)
полиномами с целыми показателями.
Уравнения второго приближения могут быть, в частности, использованы для оценки точности
первого приближения.
В заключение выражаю благодарность Б. Я. Тёмкину за полезные обсуждения настоящей работы.
|