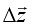При анализе процессов в электрических цепях возникает необходимость аппроксимации аналитическими зависимостями кривых намагничивания трансформаторов, сопротивлений нагрузок и др. Задача определения параметров аппроксимации сводится к решению систем нелинейных уравнений (градиентный метод, метод Ньютона и др.). Одной из ключевых проблем этих методов является обеспечение их сходимости. В данной работе решается задача улучшения сходимости метода Ньютона при решении переопределенных систем уравнений с использованием метода наименьших квадратов. При этом оптимизация величины приращения неизвестных на каждом шаге расчета осуществляется путем дополнительного вычисления функционала невязки F=Σf_i² для половины приращения неизвестных параметров (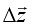), которое, в свою очередь, находится по выражению:

где W – матрица Якоби (частных производных) функции

Согласно методу определяется функционал невязки для приращения 0, 0,5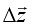 , 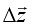и путем аппроксимации кривой второго порядка зависимости функционала F от величины шага определяется оптимальная величина шага расчета.

В качестве примера данный метод использовался для аппроксимации полученных экспериментальным путем мгновенных значений напряжений в системе собственных нужд электростанции при наличии полупроводниковых преобразователей. В качестве аналитической зависимости принята синусоида с неизвестной амплитудой, частотой и начальной фазой для мгновенных значений на заданном интервале времени.

В начало