The mathematical model of the unit of the electrical system with motors by means of including the model of the local isolation fault has been improved. The results of the parameters calculations of the operational regimes while simulating the local and distributed isolation faults are presented herein.

Для дальнейшего повышения надежности функционирования электрических систем требуется внедрение эксплуатационного мониторинга, технической диагностики и прогнозирования остаточного ресурса энергетического оборудования [1]. Значительное количество повреждений в узлах электрических систем с двигателями (УЭСД) возникает вследствие развития локальных или распределенных дефектов изоляции кабелей и обмоток электродвигателей [2-4]. Предотвратить возникновение таких повреждений можно благодаря своевременному выявлению дефектов и их устранению. Для оценки состояния кабелей и прогнозирования их работоспособности используют различные методы, например [2-5]. Основным недостатком этих методов является необходимость отключения оборудования. Обнаружение дефектов изоляции без отключения оборудования выполняют по изменению параметров рабочего режима электрооборудования [6]. Для определения возможных диапазонов изменения параметров режима и настройки средств диагностирования используют данные, получаемые экспериментальным путем и в результате математического моделирования рабочих режимов УЭСД. Однако, математическая модель, предложенная в [6], не позволяет выполнять исследования рабочих режимов при изменении места локального дефекта изоляции по длине фазы кабеля или обмотки статора электродвигателя. Кроме того, принципы отстройки средств диагностирования от внешних дефектов требуют дальнейшего совершенствования, для чего необходимо выявление закономерностей изменения параметров также путем выполнения моделирования различных рабочих режимов.

Целью работы является совершенствование математической модели УЭСД [6] для обеспечения возможности моделирования локальных дефектов изоляции при изменении их места вдоль фазы кабеля или обмотки статора электродвигателя, а также определение диапазонов изменения фазы вектора тока нулевой последовательности в зависимости от степени дефекта изоляции и от того, на какой фазе присоединения возник этот дефект. При этом также необходимо установить степень влияния на параметры режимов различных способов соединения нейтрали с землей.

За основу усовершенствованной математической модели УЭСД положена модель [6]. При этом моделирование локальных дефектов изоляции выполнено с использованием основ теории подобия [7]. В качестве основных исходных данных при моделировании используются следующие:

• схема первичных соединений узла электрической системы с двигателями;
• номинальные и другие технические данные источника питания, кабельных и воздушных линий, электродвигателей и другой нагрузки;
• конфигурация узла электрической системы в различных рабочих режимах питающей сети и технологического процесса.

  Математическое моделирование рабочих режимов узла при наличии дефектов изоляции выполняется в следующей последовательности:

• разделение элементов электрической схемы узла на характерные группы в соответствии с типичной схемой замещения, используемой в модели;
• определение комплексных продольных и поперечных проводимостей элементов узла;
• эквивалентирование параметров элементов узла в соответствии с выполненным разделением элементов по группам;
• задание диапазона изменения проводимостей для моделирования режимов с дефектами изоляции;
• выполнение расчетов рабочих режимов при изменении степени дефекта и места его возникновения.

Математическое моделирование рабочих режимов узла электрической системы с двигателями позволяет исследовать зависимость параметров режима (векторов токов фаз, векторов напряжений фаз по отношению к земле) в различных элементах узла от степени и места возникновения дефекта электрической изоляции. В модели узла имеется возможность учета различного режима нейтрали: изолированная нейтраль; соединение нейтрали с землей через дугогасящий реактор или через активное сопротивление и т.д. В схеме замещения элементы узла (линии и нагрузки) представлены комплексными продольными и поперечными проводимостями. Ведение в схему замещения продольных проводимостей элементов обеспечивает соответствие моделируемых режимов реальным режимам нагрузки.

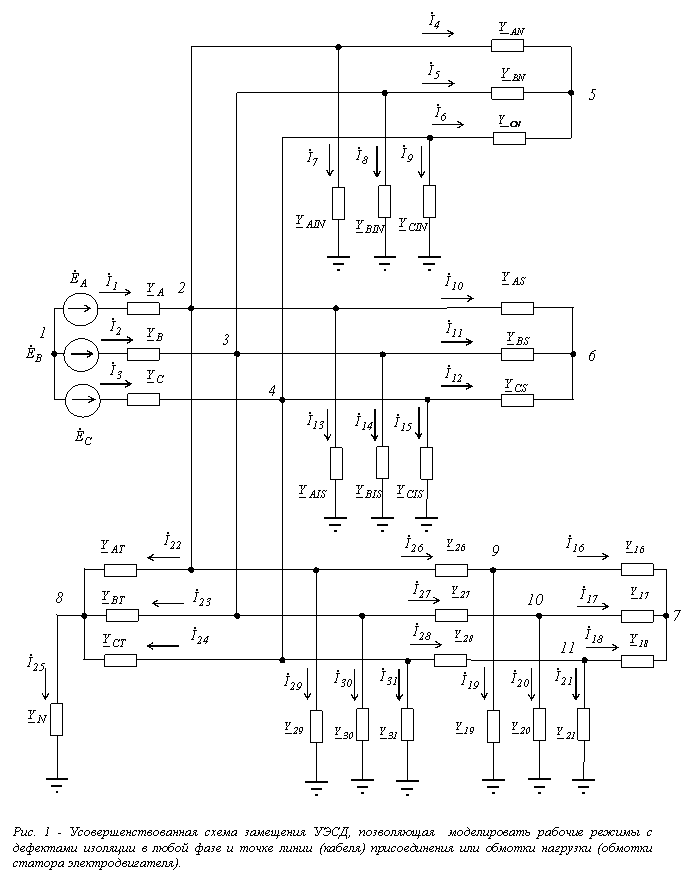
На рис.1 представлена усовершенствованная схема замещения УЭСД, которая позволяет моделировать рабочие режимы с дефектами изоляции в любой фазе и точке линии (кабеля) присоединения или обмотки нагрузки (обмотки статора электродвигателя). В схеме имеется 31 ветвь, 11 узлов и 12-м узлом является земля.

На рис.1 приняты следующие обозначения: – фазные э.д.с. и комплексные проводимости фаз источника питания; 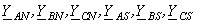– комплексные продольные проводимости фаз нагрузки соответственно присоединения без дефекта и эквивалентной группы; – комплексные проводимости изоляции фаз относительно земли соответственно присоединений без дефекта изоляции и эквивалентной группы; 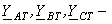– комплексные продольные проводимости фаз специального трансформатора для создания искусственной нейтрали; – комплексная проводимость между искусственной нейтралью и землей.

При моделировании локального дефекта в кабеле или в обмотке статора электродвигателя присоединения схема замещения разбивается на две части: до места дефекта и после места дефекта (рис.1). В каждой из этих частей линия (кабель) и нагрузка (двигатель) представлены Г-образной схемой замещения. Изменение параметров этих частей пропорционально расстоянию (b)от начала элемента до места дефекта (пропорционально количеству витков обмотки от ее начала до места дефекта) соответствует изменению места дефекта изоляции. Для сокращения числа узлов в схеме замещения каждой фазы присоединения с дефектом изоляции предварительно выполнены преобразования схемы соединения сопротивлений в звезду в эквивалентную схему соединения в треугольник. В результате соответствующие проводимости для фазы А (рис.1) определяются по формулам:

Здесь Z_АН и Z_АЛ – комплексные сопротивления фазы А соответственно нагрузки и линии; Z_АИН и Z_АИЛ – комплексные сопротивления изоляции фазы А по отношению к земле соответственно нагрузки и линии; Z_ДА – комплексное сопротивление дефекта изоляции фазы А.

Для фаз В и С проводимост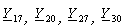и и (рис.1) определяются по таким же выражениям как и для фазы А, но с заменой индекса А соответственно на В или С.

Такая схема замещения присоединения с дефектом изоляции позволяет моделировать не только дефект изоляции в любой фазе, но также позволяет выполнять моделирование локального многофазного дефекта и одновременно учитывать реальную несимметрию продольных и поперечных параметров фаз присоединения.

Система уравнений, составленная в соответствии с методом узловых потенциалов для схемы (рис.1) , решается способом, подобно описанному в [1].

Исследования рабочих режимов проведены для схемы электроснабжения группы цехов завода, питание которых осуществляется от трансформатора типа ТРНД-40, а также для секции 6 кВ собственных нужд блока 300 МВт. Для соединения нейтрали с землей через резистор или для подключения дугогасящей катушки используется трансформатор типа ТМ-560–6/0,4, первичная обмотка которого соединена по схеме «звезда», а вторичная – по схеме «треугольник». Компенсация емкостных токов выполняется с помощью дугогасящей катушки типа РЗДПОМ-250/6. Основные результаты моделирования представлены на рис. 2 – 11.

Анализ полученных результатов показывает, что при изменении сопротивления распределенного дефекта изоляции в диапазоне от 20 до 300 кОм, величина первичного тока нулевой последовательности изменяется в диапазоне соответственно от 212 до 2,2 мА с учетом различных режимов нейтрали сети и различных величин собственной емкости контролируемых присоединений (рис.2). Чем меньше величина собственной емкости присоединения, тем больше величина тока нулевой последовательности при прочих равных условиях. При этом принято, что сопротивление изоляции «здоровых» фаз присоединений составляет 1 МОм.

При однофазных металлических замыканиях на землю как и ожидалось ток нулевой последовательности всегда больше при соединении нейтрали с землей через резистор, чем в том случае, когда нейтраль изолирована от земли. Это соотношение не зависит от величины собственной емкости рассматриваемого присоединения.

В то же время в результате исследований установлено, что в случае замыкания на землю через сопротивление при принятых параметрах схемы электроснабжения влияние режима работы нейтрали неоднозначно сказывается на величине тока нулевой последовательности. Для присоединения с максимальной собственной емкостью соединение нейтрали с землей через резистор в 100 Ом приводит к увеличению токов нулевой последовательности (кривые 1 и 3 на рис.2). Напротив, для присоединения с минимальной собственной емкостью такое соединение нейтрали приводит к снижению токов нулевой последовательности по сравнению с режимом изолированной нейтрали.

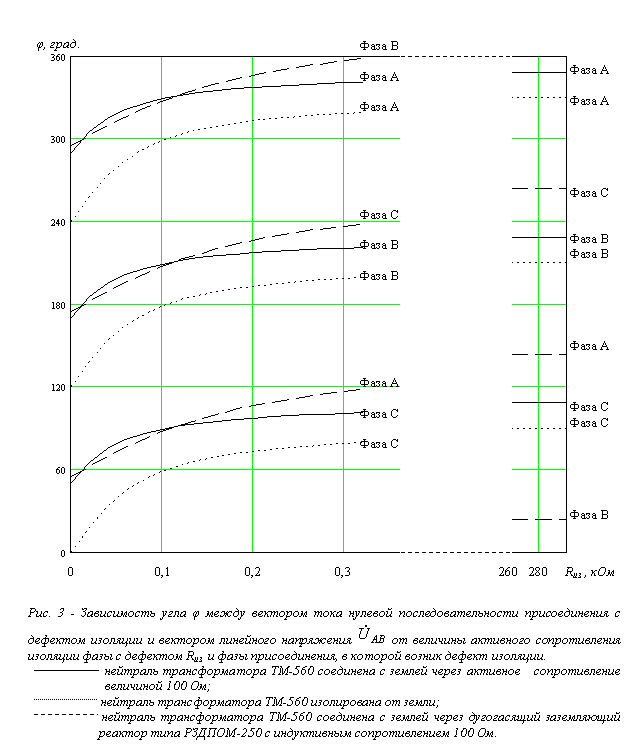
Величина угла φ между током нулевой последовательности и линейным напряжением U_АВ при возникновении распределенного дефекта изоляции на контролируемом присоединении (рис.3) зависит от величины сопротивления изоляции фазы с дефектом, а также от режима нейтрали сети и параметров оборудования, включенного между нейтралью и землей. При этом определено, что диапазон изменения угла φ не превышает 90º при моделировании дефекта и изменении его параметров в одной из фаз. Угловой сдвиг между указанными диапазонами, которые соответствуют дефектам в фазах А,В и С составляет 120º. В случае возникновения дефектов изоляции во внешней сети по отношению к рассматриваемому присоединению диапазоны изменения угла φ сдвигаются на 180º по отношению к диапазонам, которые соответствуют дефектам изоляции в фазах А,В и С на контролируемом присоединении. Таким образом, видно, что в общем случае некоторая часть диапазонов угла φ соответствует одновременно дефекту изоляции в одной из фаз контролируемого присоединения и дефекту изоляции в другой фазе во внешней сети, т.е. в этой общей области невозможно однозначно определить место возникновения дефекта.

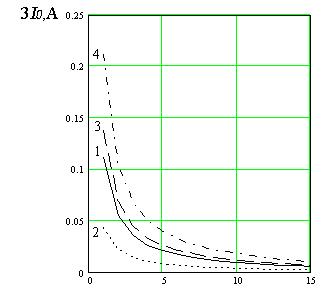
Рис. 2 - Величина тока нулевой последовательности 3I₀ в зависимости от величины сопротивления локального дефекта изоляции RД на присоединении с максимальной собственной емкостью: 1- в режиме сети с изолированной нейтралью; 2 - в режиме сети с компенсацией емкостных токов; 3 - в режиме сети с нейтралью, соединенной с землей через активный резистор; 4 – на присоединении с минимальной собственной емкостью в режиме сети с изолированной нейтралью.

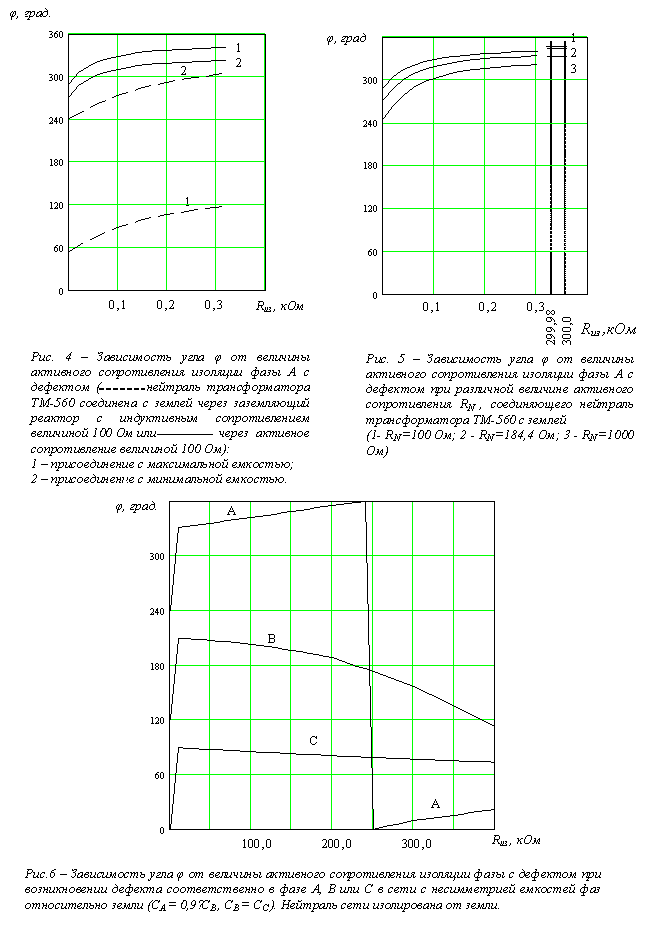
При изменении величины активного или индуктивного сопротивления, соединяющего нейтраль специального трансформатора с землей, характер зависимости φ=f(R_из) и диапазон изменения угла φ не изменяются, но при этом происходит совместное смещение диапазонов углов φ , соответствующих дефектам в фазах А,В, С, на один и тот же угол.

Степень недокомпесации емкости сети почти не оказывает влияния на угол φ . Перекомпенсация также незначительно влияет на угол φ .

Исследование зависимости параметров режима от степени и места локального дефекта изоляции в обмотке статора асинхронного двигателя привода бустерного насоса блока 300 МВт (630 кВт, 6 кВ, отношение суммарной емкости кабеля присоединения и обмотки статора к полной емкости фазы сети составляет 0,0441; основную емкость присоединения создает кабель, т.к. его емкость в 15 раз больше емкости фазы обмотки статора двигателя) позволили сделать следующие выводы.

При перемещении точки металлического замыкания на землю от линейных выводов обмотки статора к нулевым величина тока нулевой последовательности присоединения 3I₀ снижается. При резистивно заземленной нейтрали эта зависимость имеет явно выраженный нелинейный характер. При изолированной нейтрали и в случае компенсации емкостных токов зависимость 3I₀ от удаленности замыкания (b) практически линейная. По амплитуде ток 3I₀ имеет наибольшую величину в случае резистивно заземленной нейтрали.

Угол между вектором тока 3I₀ и вектором линейного напряжения U_АВ зависит от величины сопротивления дефекта изоляции, а также от режима нейтрали и практически не зависит от удаленности точки замыкания или дефекта изоляции при любом режиме нейтрали. Только в случае резистивно заземленной нейтрали при перемещении точки замыкания на землю от начала до конца обмотки угол изменяется примерно на 10º .

Амплитуда напряжения нулевой последовательности U₀ при перемещении точки дефекта от начала к концу обмотки снижается от максимального значения до нуля. В случае резистивно заземленной нейтрали и перемещении точки замыкания зависимость U₀ нелинейная.

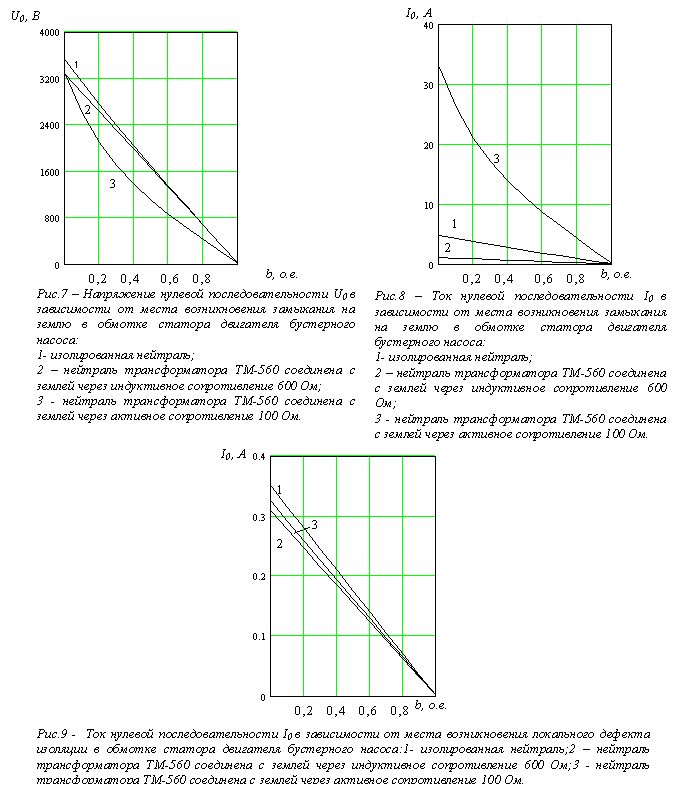
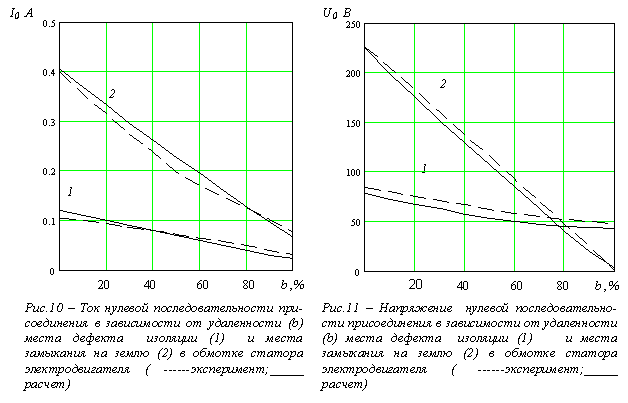
Адекватность математической модели УЭСД подтверждается на основании сопоставления результатов проведенных на физической модели опытов рабочих режимов при возникновении замыканий на землю и де-фектов изоляции в обмотке статора электродвигателя на различной удаленности дефектов от линейных выво-дов обмотки (рис.10, 11). Максимальное отличие результатов расчетов от опытных данных рабочего режима при замыкании на землю имеет место в токе нулевой последовательности и составляет 16,8 % при замыкании в середине обмотки и 14,5 % - при замыкании вблизи нулевых выводов. При замыканиях во всех остальных точках обмотки отличие не превышает 9,6 %. При моделировании дефектов изоляции значения отличий расчетных и опытных данных токов и напряжений имеют примерно такие же значения, как и при замыканиях. Основной причиной отличий опытных и расчетных данных является приближенный учет в математической модели имеющейся несимметрии продольных и поперечных проводимостей фаз физической модели в режиме без де-фектов изоляции. Такой учет обусловлен сложностью точного определения несимметрии.

Выводы

1. Предложена усовершенствованная математическая модель узла электрической системы с двигателями, позволяющая выполнять моделирование рабочих режимов присоединений в случае возникновения распределенных и локальных дефектов изоляции. Адекватность модели подтверждена сравнением расчетных и опытных данных.
2. На основании математического моделирования рабочих режимов в узлах электрических систем с двигателями получены зависимости параметров режимов присоединений кабель-нагрузка от степени дефекта изоляции и места его возникновения, позволяющие разрабатывать принципы выявления локальных и распределенных дефектов изоляции.
3. Определены зависимости величины тока нулевой последовательности, а также угла сдвига фаз между вектором тока нулевой последовательности и вектором линейного напряжения от степени и места возникновения дефекта изоляции.

ЛИТЕРАТУРА

1. Шидловський А.К., Федоренко Г.М. Енергетичний комплекс України на сучасному етапі // Технічна електродинаміка. Тематичний випуск: Проблеми сучасної електротехніки. Частина 1. 2004. – С. 3- 6.
2. Лебедев Г.М., Бахтин Н.А., Брагинский В.И. Математическое моделирование локальных дефектов изоляции силовых кабелей 6-10 кВ //
3. Корогодский В.И., Кужеков С.Л., Паперно Л.Б. Релейная защита электродвигателей напряжением выше 1 кВ.- М.: Энергоатомиздат, 1987.- 248 с.
4. Трост Л.Е. Методические указания по разборке, осмотру и определению причины отказа кабельной арматуры, установленной на кабелях с бумажной пропитанной изоляцией на напряжение 1 –10 кВ .- М.: Энергоатомиздат, 1996. 80 с.
5. Muhr M., Strobl R., Woschsitz R. Entladestrommethode – Ein Prufverfahren fur kunststoffisolierte Mittelspannungskabel // Elektrotechn. und Informationstechn. – 1998 .- 115, № 6 . – C. 321 – 326.
6. Гребченко М.В.Теоретичні основи побудови захисно-діагностуючої автоматики вузлів електричних систем з двигунами. Частина 2. Функції оперативного діагностування ізоляції електрообладнання// Збірник наукових праць Донецького національного технічного університету. Серія: Електротехніка і енергетика, випуск 50: Донецьк: ДонНТУ. - 2002. – С.53-61.
7. Веников В.А., Веников Г.В. Теория подобия и моделирования (применительно к задачам электроэнергетики). – М.: Высш. шк., 1984 .- 439 с.

В начало