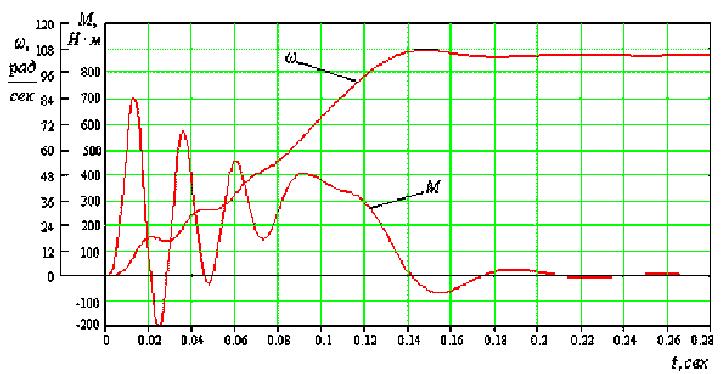
Рис.4. Результаты расчета по разработанной методике
Область применения регулируемых электроприводов переменного тока и в нашей стране, и за рубежом в
значительной степени расширяется. Особенно это относится к асинхронным электроприводам со
статическими преобразователями энергии и двигателями с короткозамкнутым ротором. Эта тенденция
обусловлена в большей мере конструктивной простотой и надежностью такого типа двигателей, а также
технологичностью их изготовления, сравнительно низкой стоимостью и удобством в эксплуатации.
Однако двигатель, как объект автоматического управления представляет собой сложную динамическую
структуру, описываемую системой нелинейных дифференциальных уравнений высокого порядка. По
этой причине применение такого описания в разработках систем управления асинхронным
электроприводом в большинстве случаев оказывается проблематичным. Практически, чаще всего в
задачах управления пользуются упрощенными линеаризованными вариантами динамических моделей,
что приводит на практике к ухудшению качества процессов регулирования координат асинхронного
электропривода.
Вопросы разработки динамических моделей асинхронного двигателя неоднократно ставился в работах
[5, 6]. Однако существующие модели в ряде случаев дают существенные ошибки. В то же время в связи
расширением области применения, особенно высокоточных электроприводов требуются уточненные
модели.
Таким образом, разработка математического описания электромагнитных и электромеханических
процессов в асинхронном электроприводе, учитывающих реальный характер нелинейных процессов в
асинхронном электродвигателе при условии максимального снижения порядка дифференциальных
уравнений, а также использование такой структуры математического описания при разработке
регулируемых асинхронных электроприводов, представляется актуальной.
Вывод уравнений описывающих электромагнитные и электромеханические процессы в асинхронном
электроприводе, учитывающих нелинейный характер протекания процессов в двигателе осуществлен в
[1, 3].

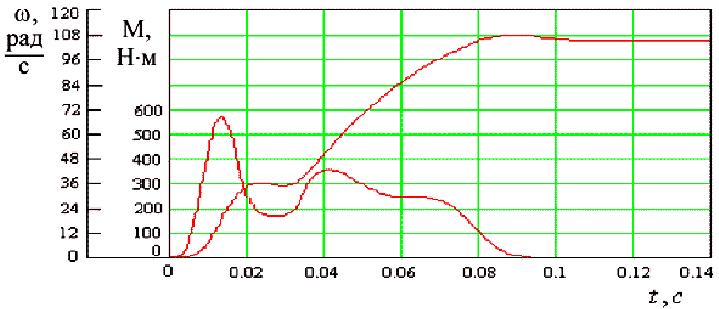
Сопоставление результатов показало, что реальные диаграммы скорости и момента получаемые в режиме прямого пуска асинхронного двигателя существенно отличаются от результатов получаемых при расчете по уравнениям Парка-Горева. Для двигателя МТВ 311-6 расхождение расчетного времени пуска по уравнениям (9)-(17) с экспериментом составляет 12%, тогда как время пуска по уравнениям Парка-Горева в два раза превышает эксперимент. Пусковой момент при расчете по предложенной методике отличается от эксперимента на 7%, расхождение при расчете по уравнениям Парка-Горева составляет 15%. Количество пульсаций момента при пуске при расчете по изложенной в работе методике совпадают и составляют 2, тогда как при классической методике момент имеет 4-5 пульсаций.
Таким образом новая модель асинхронного двигателя, полученная на основе тензорного анализа и позволяющая осуществлять учет нелинейного характера протекания электромагнитных процессов в двигателе при переменной частоте вращения уточняющая расчеты по различным показателям на 6-25% в зависимости от мощности используемого двигателя.
1. Архангельский Н. Л., Курнышев Б. С, Захаров П. А. Применение тензорной методологии к
описанию электромагнитных процессов в асинхронном двигателе. - М.: Энергоатомиздат,
Электричество, 1995, № 2. - С. 37-39.
2. Захаров П. А. Расчет установившихся режимов асинхронного электропривода. - В сб.:
Электрооборудование промышленных установок. - Н.Новгород: НГТУ, 1996. - С. 79 - 84.
3. Захаров П. А. Расчет переходных процессов в асинхронном электроприводе с использованием
тензорной методологии. - В сб: Оптимизация режимов работы систем электроприводов. -
Красноярск: КГТУ, 1997. - С. 33 - 37.
4. Крон Г. Применение тензорного анализа в электротехнике. - М.-Л.: Госэнергоиздат, 1955. - 276 с.
5. Петров Л.П. Управление пуском и торможением асинхронного двигателя. - М.: Энергоатомиздат,
1981. - 184 с.
6. Электромагнитные переходные процессы в асинхронном электроприводе / Соколов М. М.,
Петров Л. П. Масандилов Л. Б., Ладензон В. А. - М. : Энергия, 1967. - 200 с.
7. Чиликин М. Г., Соколов М. М., Терехов В. М., Шинянский А. В. Основы автоматизированного
электропривода. - М.: Энергия, 1974. - 568 с.