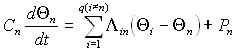, (1)Частые выходы из строя приводного двигателя кантователя свидетельствуют о том, что реальные режимы работы механизма не соответствуют паспортным режимам двигателя. Особенно это наглядно при прокатке круга “80”, когда число включений двигателя может достигать 800-1000 в час.
Для предотвращения преждевременного выхода из строя необходимо контролировать его тепловое состояние или уметь рассчитать температуру наиболее нагретых элементов двигателя при заданном характере нагружения. Контроль теплового состояния реального двигателя затруднен, поэтому основное внимание уделим его расчету на базе эквивалентной тепловой схемы замещения (ЭТСЗ). Данный метод основан на замене двигателя, состоящего из n-элементов с присущими каждому элементу удельной теплоемкостью и теплоотдачей, системой с конечным числом расчетных тел. Обычно, в практических расчетах, число расчетных тел принимается равным двум, пяти, семи, не превышают этих чисел и тепловые аналоги, используемые в схемах защиты двигателей.
Тепловое состояние n-го тела может быть описано следующим уравнением:
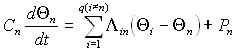, (1)
где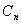 
–теплоемкость n-го тела;
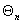– температура n-го тела;
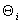– температура одного из соседних тел i; q – количество тел,
связанных в тепловом отношении с рассматриваемым телом n;
–
теплоотдача от одного из соседних тел i к данному телу n;
–
потери мощности в данном теле n; t – текущее время.
Для системы из n тел уравнения теплового баланса будут иметь следующий вид:
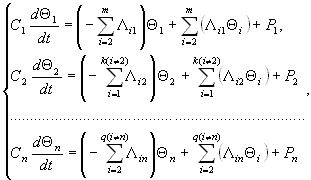(2)
где m – количество тел, связанных в тепловом отношении с первым телом; k –количество тел, связанных в тепловом отношении со вторым телом.
Решение данной системы приводит к определению средней температуры
n-го тела в момент времени t.
Уравнения теплового баланса целесообразно привести к виду:
(3)
где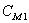 
, 
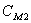– полные теплоемкости обмоток статора и ротора;
, 
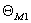– текущие значения температур обмоток;
, 
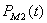– текущие значения электрических потерь в обмотках статора и ротора.
При исследовании динамики асинхронного электропривода его поведение описывается следующей системой дифференциальных уравнений:
(4)
Выражение для электрических потерь имеет вид:
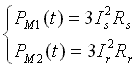(5)
где ,
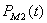– текущие значения электрических потерь в обмотках статора и ротора, Is, Ir – действующие значения токов статора и ротора, Rs, Rr – активные сопротивления обмоток статора и ротора.
Мгновенные значения токов в обмотках электрической машины находим из системы уравнений (6), имеющей вид.
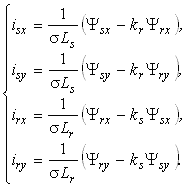(6)
Действующие значения токов для подстановки в (5) получаем из 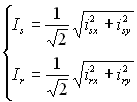(7).
(7)
Зная текущие потери в статоре и роторе, можно перейти к определению температур обмоток и с помощью (3).
При исследовании пускового режима температура обмоток и находятся при совместном решении (3) и (5).
В дальнейшем они используются как начальные условия при исследовании теплового состояния двигателя при конкретном характере нагружения.
Блок-схема алгоритма решения задачи приведена на рис.1
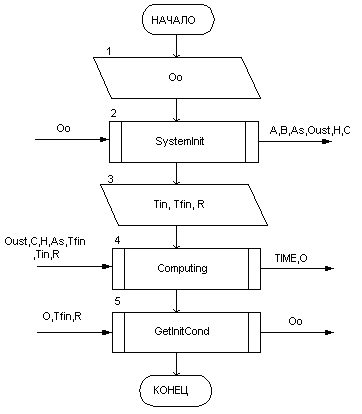
Рисунок 1. Алгоритм расчета температур элементов ЭТЗС.
Программа представляет собой m-файл, реализованный в среде Matlab. Принятая схема расчета температур тел ЭТСЗ удобна для анализа теплового состояния двигателя в длительном и циклических режимах.
Литература:
1. Нестационарные тепловые расчеты в электрических машинах. Беспалов В.Я., Дунайкина Е.А., Мощинский Ю.А./ Под ред. Б.К. Клокова.–М.:Моск.энерг. ин-т, 1987.–72с.