
Асинхронная машина является индукционной, т.е. машиной переменного тока, не имеющей связи между статором и ротором. Определение индукционной машины иногда употребляется, но этот термин изначально англо-саксонский.
Машина состоит из двух основных частей:
Эта машина может быть, в зависимости от конструкции, подключена к одно- или многофазной сети (в основном трехфазной)
Асинхронная машина является наиболее использованной в диапазоне мощностей от нескольких киловатт и выше, так как она представляет собой наилучшее сочетание цены-качества. Популярность увеличилась, когда в 1980 году появились регуляторы скорости, позволяющие изменять в широком диапазоне скорость вращения двигателя.
Хотя машина может быть реверсирована, все же чаще она используется как двигатель, а не генератор.
Токи статора создают в статоре вращающееся магнитное поле. Это поле синхронно по частоте с токами статора, то есть скорость вращения пропорциональна частоте подводимой электрической сети. Скорость вращающегося поля называется синхронной скоростью.
Таким образом, обмотки ротора подвержены изменениям потока (магнитного поля). Появишаяся электродвижущая сила создает ток в роторе. Эти токи приводят к появлению момента сил Лапласа, приводящих ротор в движение, противоположное изменению потока : закон Ленца. Таким образом, ротор начинает вращаться, увлекаемый полем статора.
Машина называется асинхронной поскольку она не может достигнуть без внешних воздействий той же скорости вращения, что и поле статора. Разница между скоростью вращения ротора и магнитного поля статора называется скольжением.
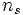
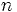
Синхронная скорость кратна частоте питающей сети
Либо кратна числу пар полюсов машины и частоте подводимой сети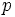 ,
,
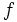
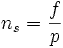 в об/мин
в об/мин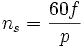 в об/мин
в об/мин
Скольжение соответвтвует разнице скорости ротора и поля статора и выражено в процентном соотношении к синхронной скорости.
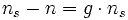 ,
или
,
или 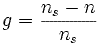
Значение скольжение довольно мало. Порядка 2 % для более мощных машин и 6 или 7 % для малых мощностей трехфазных машин. Может достигнуть 10 % для небольших однофазных машин.
Состоит из ферромагнитного цилиндра с пазами, позволяющими поместить в них обмотку. Єтот цилиндр состоит из шихтованных пластин, которые уменьшают токи Фуко.
Статор трехфазной мошины включает 3 обмотки.


Различают 3 вида роторов :
Лишь исходя из заданной нагрузки, напряжения и полных сопротивлений сложно рассчитать токи машины и вывести из них моменты и скорости вращения.
Проще начать с конца. Таким образом, считаем, что токи нам известны. Из выражений токов статора и ротора выводим выражения для магнитных потоков. Зная потоки и токи машины можно записать уравнения напряжений, применяя закон Ома и Фарадея.
Рассматривается машина с одной парой полюсов.
угол 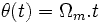 соответствует угловому смещению между статором и ротором:
соответствует угловому смещению между статором и ротором:
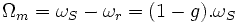
Предположения: Магнитный контур однородный и ненасыщенный. Индуктивности постоянны.
Фиксируем начальный момент времени:
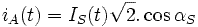
Отсюда выводим значения токов статора двух остальных фаз:
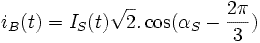
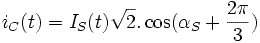
при: 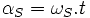 ,
и
,
и 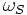 :
частота токов статора
:
частота токов статора
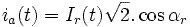
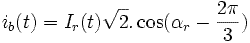
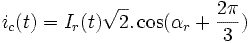
при: 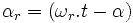 ,
,
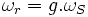 :
частота токов статора, и
:
частота токов статора, и 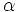 = начальная фаза тока
= начальная фаза тока 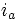 .
.
Notations :
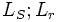 :
Собственные индуктивности обмотки статора; ротора.
:
Собственные индуктивности обмотки статора; ротора.
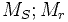 :
Взаимные индуктивности между двумя обмотками статора; ротора.
:
Взаимные индуктивности между двумя обмотками статора; ротора.
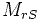 :
Максимальное значение взаимной индуктивности между обмоткамиротора и статора (соответствует положению θ = 0 ± 2π/3 .
:
Максимальное значение взаимной индуктивности между обмоткамиротора и статора (соответствует положению θ = 0 ± 2π/3 .
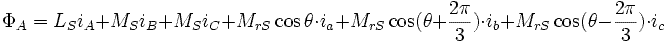
Выражение не изменится, если добавим: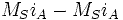
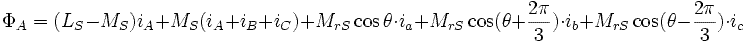
Так как : :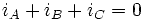
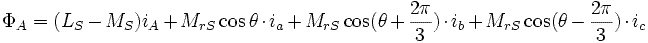
заменяем :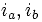 и
и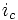 их выражениями и используя :
их выражениями и используя :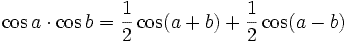
![\Phi_A = (L_S - M_S) i_A + M_{rS} I_r \sqrt{2} \left\{ \frac{3}{2} \cdot \cos (\theta + \alpha_r) + \frac{1}{2} \cdot \left[ \cos (\theta - \alpha_r) + \cos (\theta - \alpha_r - \frac{2 \pi}{3}) + \cos (\theta - \alpha_r + \frac{2 \pi}{3}) \right] \right\}\,](8d69a9b1bf6c2f0839dc40a0a0fd5c7c.gif)
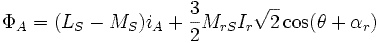
Or 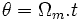 ,
, 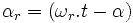 et
et 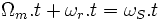
В результате получаем :
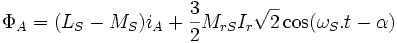
Полагаем:
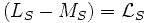 :
циклическая индуктивность
:
циклическая индуктивность
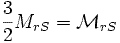 :
взаимная циклическая индуктивность
:
взаимная циклическая индуктивность Также полагаем:
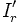 :
Условный ток эффективного значения
:
Условный ток эффективного значения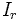 но с частотой
но с частотой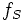
Выражение для потока упрощается. Применяем комплексное преобразование и получаем комплексное выражение для потока фазы статора:
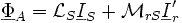 с частотой
с частотой 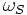
Расчет потока ротора проводится идентично предыдущему, но с разницей в знаках.
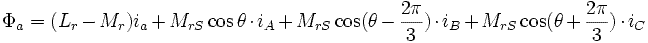
При введении в выражение циклических значений
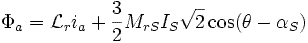
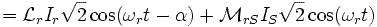
Выражение запишется:
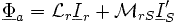 с частотой
с частотой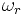
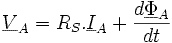
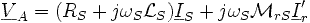
Короткозамкнутый ротор.
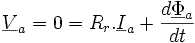
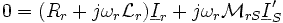
Так как 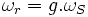 ,
получаем :
,
получаем :
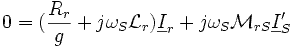
Полезная электромагнитная мощность соответствует в каждой фазе мощности, потребленной сопротивлением 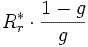
Полная электромагнитная мощность будет описана выражением вида:
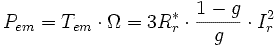
Следующая модель позволяет получить выражение зависимости момента от скольжения и скорости. Расчет очень упрощен и может быть выполнен вручную, если пренебречь сопротивлением статора. В этом случае погрешность ошибки будет составлять 2-3%, но полученные кривые близки к реальным.
В рамках такого приближения получим :
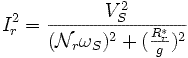
При 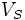 :
эффективное значение напряжения на зажимах одной фазы статора.
:
эффективное значение напряжения на зажимах одной фазы статора.
Зависимость будет иметь вид :
для машины с p парами полюсов имеем : 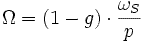
Из этого следует :
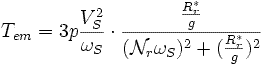
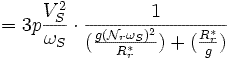
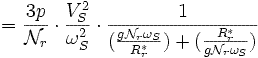
Электромагнитный момент проходит через максимум при :
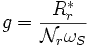
Зависимость момента от скольжения представлена симметрично по отношению к началу координат :
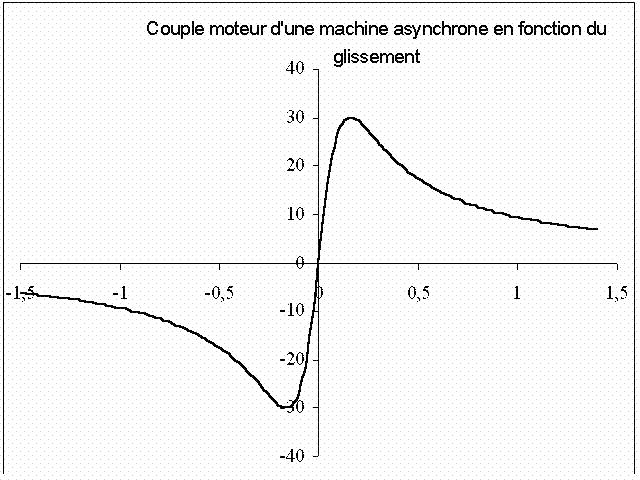
Эта зависимость более привычна. Она выводится просто из соотношения :
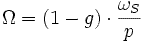
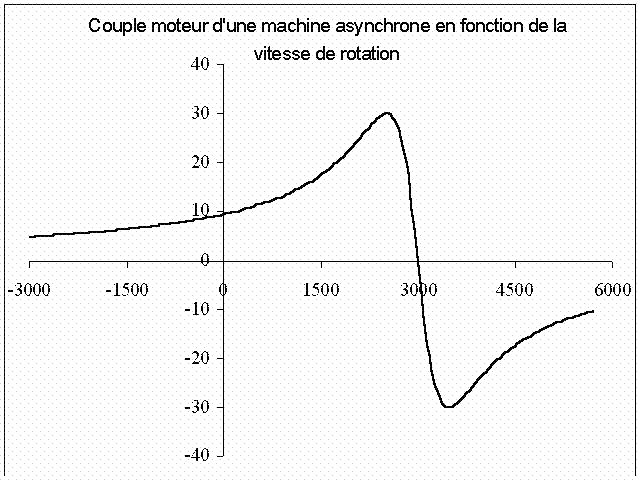
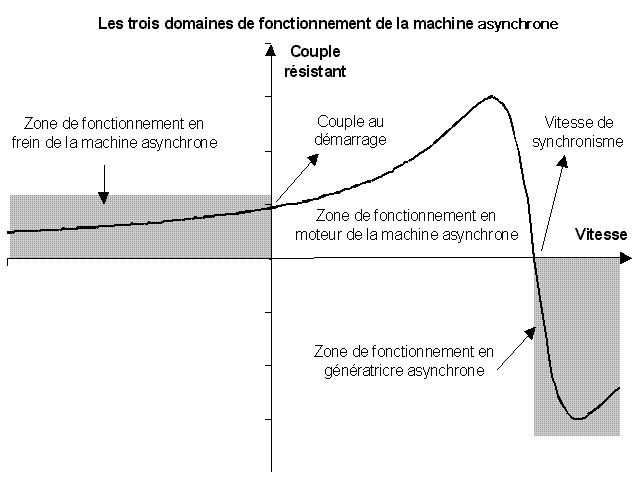
Регулирование скорости вращения асинхронного трехфазного двигателя
Регуляторы скорости с широтно-импульсной модуляцией - это тот вид управления, который позволяет сохранить соотношение U1/f.
Чтобы понять принцип управления U/f, необходимо обратиться к уравнению момента.
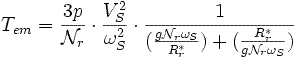
Cmax - максимальный момент.
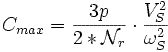
Перепишем отношение поток/напряжение по отношению к потоку.
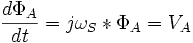
Φs - эффективное значение номинального потока.
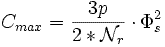
Если сохраняется соотношение 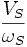 , то можно заменить скорость при которой достигаетсяCmax.
Выражение приобретет вид t:
, то можно заменить скорость при которой достигаетсяCmax.
Выражение приобретет вид t:
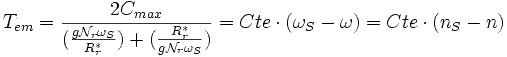
Зависимость момента от nS - n
при запуске с большим пусковым моментом падение напряжения на сопротивлении статора становится больше ЭДС. Таким образом невозможно получить номинальный поток машины благодаря закону U/f=cst. Чтобы это скомпенсировать заводские регуляторы предусматривают различные зависимости U(f). Выборзависит от применения области машины.
В ходе изменения скорости асинхронного двигателя становится генератором гармоник.
Применяют для улучшения характеристик двигателя.