В большинстве асинхронных двигателей необходимо обеспечить высокий КПД. Поэтому активное сопротивление обмоток, в частности R₂, определяющее уровень электрических потерь в роторе, стремятся получить малым. При этом критическое скольжение лежит в диапазоне [0,1..0,25].
   Подставляем (2.25) в (2.22) и получаем выражение максимального момента:

M_max= ± m₁U₁² /2 ω ₁C·[± R₁ + √(R₁² +(x₁ +Cx₂)²)]    (2.27)

Знак "+" относится к двигательному режиму, "-" – к генераторному.
Как видно, максимальный момент пропорционален квадрату напряжения питания, не зависит от активного сопротивления роторной цепи R₂ и наступает при тем большем скольжении, чем больше активное сопротивление роторной цепи (рис. 2.11, штрих-пунктирная линия, R_2B>R_2A).
   Пусковой момент двигателя M_п определяется выражением (2.22) при s=1. Значение M_п пропорционально квадрату напряжения питания и возрастает при увеличении R₂ (см. рис. 2.11), достигая максимума при s_кр =1.
   Номинальное скольжение sном, соответствующее номинальному моменту Мном,возрастает с увеличением R₂. Это сопровождается ростом электрических потерь в роторной цепи и снижением КПД. У асинхронных двигателей с малым критическим скольжением S_ном= 0,02 - 0,06.

Уравнение равновесия моментов на валу двигателя.
    Электромагнитный момент, развиваемый двигателем, преодолевает мо-мент нагрузки М_н, прикладываемый к валу двигателя, и собственный момент сопротивления двигателя М₀ (момент холостого хода), определяемый механическими и добавочными потерями в двигателе. Результирующий момент определяет значение и знак ускорения ротора:

Roman, Times, serif">dω/dt = (M_эм - M₀ - M_н) /J   (2.28)

где J - момент инерции вращающихся частей – ротора и на-грузки.
   Это диффиренциальное уравнение движения электропривода, состоящего из двигателя и нагрузки, преобразованное к виду

M_эм = M₀ + M_н + J(dω/dt)   (2.29)

называют уравнением равновесия моментов на валу двигателя.
   В этом уравнении:
M₀ + M_н= M_ст - статический момент сопротивления,
J(dω/dt)= M_дин - динамический момент сопротивления.
Электромагнитный момент M_эм за вычетом момента M₀ называют полезным или вращающим моментом на валу и обозначают M₂. Из уравнений (2.28) и (2.29) следует, что:
1) если M_эм = M_ст, то dω/dt = 0, ω = const т.е. двигатель работает в установившемся (статическом) режиме, при этом M₂ = M_н;
2) если M_эм> M_ст, то угловая скорость ротора возрастает, т.е. двигатель работает в переходном ( динамическом ) режиме;
3) если M_эм< M_ст, то угловая скорость ротора убывает, т.е. двигатель работает в переходном режиме.
   В общем случае при составлении уравнения равновесия моментов следует учитывать знаки моментов, которые определяются направлением действия моментов по отношению к положительному направлению вращения. Если двигатель создает электромагнитный момент, действующий в положительном направлении, то момент считается положительным (M_эм> 0). Если двигатель переходит в тормозной режим, его момент начинает действовать в противоположном направлении (M_эм< 0).
   Статические моменты сопротивления, создаваемые рабочим механизмом и передаточным устройством, бывают двух видов:реактивные и активные, или потенциальные. Реактивные моменты сопротивления всегда направлены против направления вращения, т.е. являются тормозными (M_ст< 0). К реактивным моментам относятся моменты сил трения, в том числе в самом двигателе, моменты сопротивления при резании металла на обрабатывающих станках и т.д. Активный момент всегда действует в одном и том же направлении, независимо от направления вращения, т.е. может либо препятствовать движению (M_ст> 0), либо способствовать ему (M_ст< 0). К активным моментам относятся моменты сил тяжести, сил упругости пружин и т.д.

Механические характеристики.
    Уравнением естественной механической характеристики асинхронного двигателя является выражение (2.21) или (2.22) с заменой скольжения S на угловую скорость ω₂ по (2.8) при U₁= const. График характеристики изображен на рис. 2.12,а.

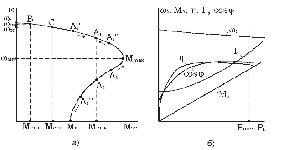
Рис.2.12

Оценим механическую характеристику по показателям устойчивости, жесткости и линейности.
   Считается, что двигатель в разомкнутом приводе работает устойчиво, если после снятия возмущения он автоматически возвращается в исходную рабочую точку на механической характеристике. Механическая характеристика двигателя представляет собой зависимость угловой скорости ротора от электромагнитного момента: ω₂= f(M_эм).Механической характеристикой нагрузки является зависимость статического момента сопротивления на валу двигателя от угловой скорости: M_ст = f(ω₂).
   Теоретически установившийся режим работы двигателя возможен в точках А₁ и А₂, где M_эм=M_ст.А. Пусть двигатель работает с нагрузкой M_ст.А=const в точке А₁ и появляется возмущение, приводящее к увеличению угловой скорости ??. Тогда двигатель создает вращающий момент, соответствующий точке А₁', а нагрузка – момент сопротивления, соответствующий точке А₁. При этом M_эм< M_ст, в соответствии с уравнением равновесия моментов угловая скорость ω₂ уменьшается и двигатель возвращается в точку А₁. Возврат в точку А₁ будет происходить и при отрицательном приращении скорости (точка А₁'' ). Если двигатель работает c нагрузкой в точке А₂, то при возмущении, приводящем к увеличению скорости, двигатель создает вращающий момент, соответствующий точке А₂', а нагрузка – момент сопротивления, соответствующий точке А₂. При этом M_эм>M_ст и угловая скорость продолжает увеличиваться, двигатель уходит от точки А₂. Возврата в точку А₂ не происходит и при отрицательном приращении скорости (точка А₂'' ). В этом случае скорость будет продолжать уменьшаться вплоть до остановки двигателя.
   Следовательно в точке А₁ двигатель работает устойчиво, а в точке А₂ – неустойчиво. В общем случае, формальным признаком устойчивой работы двигателя является неравенство

(dM_эм /dω₂) < (dM_ст /dω₂)   (2.30)

При моменте нагрузки, не зависящем от скорости, т.е. при M_ст= const, это неравенство принимает вид

(dω₂ /dM_эм) < 0   (2.31)

Исходя из понятия устойчивости работы двигателя в разомкнутом приводе, принято называть механическую характеристику двигателя устойчивой, если она обеспечивает устойчивую работу двигателя при M_ст= const.
   Если воспользоваться формальным признаком устойчивости (2.31), то легко показать, что при M_ст= const устойчивая работа двигателя обеспечивается только на участке от ω₁ до ω_2кр. Участок от ω_2кр до 0 является неустойчивым. Рабочий диапазон моментов и скоростей электроприводов с асинхронными двигателями выбирается в пределах устойчивой части механической характеристики двигателя. Точка номинальной нагрузки M_ном располагается на рабочем участке таким образом, чтобы перегрузочная способность K_m= М_max /М_ном= 1,7 –3,5. При малом сопротивлении ротора R₂ критическая скорость ω_2кр=(0,8 – 0,9)ω₁ и рабочий участок жесткий. Механическая характеристика в целом нелинейная, но ее рабочий участок близок к линейному.
   В пределах рабочего участка происходит саморегулирование двигателя. Увеличение момента сопротивления на валу двигателя от M_ст.в до M_ст.с приводит к уменьшению угловой скорости ротора от ω_2в до ω_2с, увеличению ЭДС и тока, наводимых в роторе вращающимся полем, и, соответственно, росту электромагнитного момента до значения, равного новому значению момента сопротивления (переход из точки В в точку С на механической характеристике).

Рабочие характеристики.
   Рабочие характеристики асинхронного двигателя - это зависимости угловой скорости ротора ω₂, полезного момента М₂, КПД η, коэффициента мощности cos φ₁(φ₁ - сдвиг по фазе между U₁ и I₁) и тока статора I₁ от полезной мощности Р2 при U₁ = U_ном и f₁ = f_ном (рис.2.12,б). Рабочие характеристики могут быть либо сняты экспериментально, либо рассчитаны с использованием схемы замещения.
   При переходе от режима х.х. (двигатель не нагружен) к режиму номинальной нагрузки угловая скорость ротора снижается незначительно, т.к. ω₂=(1 - s)ω₁, а S_ном, как отмечалось, составляет единицы процентов. Соответственно, полезный момент М₂= P₂ /ω₂ возрастает по закону, близкому к линейному. Изменение тока статора определяется реакцией ротора; относительно большое значение тока при холостом ходе объясняется наличием воздушного зазора. Ток х.х. в основном индуктивный, и соответственно низок cos φ₁₀ – порядка 0,1 – 0,2. По мере роста нагрузки возрастает потребляемая активная электрическая мощность и cos φ₁ растет – его максимальное значение достигает 0,7 - 0,9. Ток сохраняет активно-индуктивный характер ( φ₁>0 ) и питающая сеть загружается реактивным током. КПД двигателя η= Р₂ /Р₁, где Р₁ – активная электрическая мощность, потребляемая двигателем. При симметричном питании Р₁ = m₁U₁I₁cos φ₁, где U₁, I₁ – фазные напряжение и ток. Зависимость КПД от мощности Р₂= Р₁ -Δp_э -Δp_м -Δp_мех имеет такой же вид, как и у трансформатора, т.к. в двигателе потери также подразделяются на постоянные и переменные. Для машин малой и средней мощности максимальное значение КПД η = 0,7 – 0,9, при этом меньшие значения относятся к двигателям меньшей мощности, у которых относительно больше активное сопротивление обмоток.